Dipolar order mediated ¹H → ¹³C cross-polarization for dissolution-dynamic nuclear polarization

Magnetic resonance imaging and spectroscopy often suffer from a low intrinsic sensitivity, which can in some cases be circumvented by the use of hyperpolarization techniques. Dissolution-dynamic nuclear polarization offers a way of hyperpolarizing ¹³C spins in small molecules, enhancing their sensitivity by up to 4 orders of magnitude. This is usually performed by direct ¹³C polarization, which is straightforward but often takes more than an hour. Alternatively, indirect ¹H polarization followed by ¹H→¹³C polarization transfer can be implemented, which is more efficient and faster but is technically very challenging and hardly implemented in practice. Here we propose to remove the main roadblocks of the ¹H→¹³C polarization transfer process by using alternative schemes with the following: (i) less rf (radiofrequency) power; (ii) less overall rf energy; (iii) simple rf-pulse shapes; and (iv) no synchronized ¹H and ¹³C rf irradiation. An experimental demonstration of such a simple ¹H→¹³C polarization transfer technique is presented for the case of [1-¹³C]sodium acetate, and is compared with the most sophisticated cross-polarization schemes. A polarization transfer efficiency of ∼0.43 with respect to cross-polarization was realized, which resulted in a ¹³C polarization of ∼8.7 % after ∼10 min of microwave irradiation and a single polarization transfer step.

1 Introduction

Traditional magnetic resonance imaging (MRI) and spectroscopy (MRS) experiments usually suffer from low sensitivity. Hyperpolarization techniques including dissolution-dynamic nuclear polarization (dDNP) can be used to highly polarize a large variety of chemical systems and therefore enhance nuclear magnetic resonance (NMR) signals by several orders of magnitude (Ardenkjær-Larsen et al., 2003). Various applications of dDNP have been demonstrated, including the study of enzyme kinetics, cell extracts and heteronuclear metabolomics (Bornet et al., 2014b, 2016a; Dumez et al., 2015). Most dDNP applications involve the use of weakly magnetic isotopes such as ¹³C, but excessively long DNP timescales τ_DNP(¹³C) hinder efficient polarization build-up and lead to extended experimental times. Intrinsically sensitive proton nuclear spins do not suffer from such issues and can be polarized quickly and to a greater extent at low temperatures (Hartmann et al., 1973).

The use and optimization of cross-polarization (CP) under dDNP conditions (typically at temperatures of about 1.2–1.6 K in superfluid helium) provides a way to substantially boost ¹³C polarizations and enhance build-up rates 1∕τ_DNP(¹³C) (by a factor of up to 40) (Hartmann and Hahn, 1962; Pines et al., 1972; Perez Linde, 2009; Jannin et al., 2011; Bornet et al., 2012, 2013; Batel et al., 2012; Vuichoud et al., 2016; Cavaillès et al., 2018). The technique requires intense B₁ matching (typically > 15 kHz) of simultaneous ¹H and ¹³C spin-locking radiofrequency (rf) fields throughout an optimized contact period (typically > 1 ms). This CP-DNP approach recently turned out to be key for the preparation of transportable hyperpolarization (Ji et al., 2017), where samples are polarized in a CP-equipped polarizer and then transported over extended periods (typically hours or days) to the point of use.

This CP approach was demonstrated on typical dDNP samples back in 2012 (Bornet et al., 2012); however, the technique remains challenging today because of its methodological and technical complexity. Indeed, CP under dDNP conditions employs sophisticated pulse sequences, and involves high-power and high-energy rf pulses. Another drawback of CP-DNP is that it can hardly be scaled up to volumes larger than 500 µL, otherwise engendering detrimental arcing in the superfluid helium bath (Vinther et al., 2019). Such scaling-up would be required to enable parallel hyperpolarization of multiple transportable samples (Lipsø et al., 2017), and for volumes > 1 mL currently used for hyperpolarized human imaging (Nelson et al., 2013).

For hyperpolarizing larger sample volumes, alternative rf sequences with reduced power requirements are desired. Lower-power alternatives to CP have previously been described in the literature (Jeener et al., 1965; Jeener and Broekaert, 1967; Redfield, 1969; Kunitomo et al., 1974; Demco et al., 1975; Emid et al., 1980; Vieth and Yannoni, 1993; Zhang et al., 1993; Kurur and Bodenhausen, 1995; Lee and Khitrin, 2008; Khitrin et al., 2011; Vinther et al., 2019), which rely on indirect polarization transfer via proton dipolar order rather than through a direct ¹H–¹³C Hartman–Hahn matching condition (Hartmann and Hahn, 1962).

The population of a Zeeman eigenstate for a spin-1∕2 nucleus at thermal equilibrium ${\mathit{\rho }}_{\mathrm{eq}}^i$ is given as follows:

$$\begin{array}{}\text{(1)}& {\mathit{\rho }}_{\mathrm{eq}}^i={\displaystyle \frac{\exp \left\{-\frac{\mathrm{\hslash }{\mathit{\omega }}_i}{{\mathit{\kappa }}_{B}T}\right\}}{Z}},\end{array}$$

where ω_i is the energy of the state for the spin of interest, T is the temperature and Z is a canonical partition function. In the high-temperature limit, the spin density operator ${\widehat{\mathit{\rho }}}_{\mathrm{eq}}$ (which describes the state of an entire ensemble of spin-1∕2 nuclei at thermal equilibrium) is expressed by using a truncated Taylor series:

$$\begin{array}{}\text{(2)}& {\widehat{\mathit{\rho }}}_{\mathrm{eq}}\simeq \widehat{\mathrm{1}}+\mathbb{B}\sum _i{\widehat{I}}_{iz},\end{array}$$

where $\mathbb{B}=\mathrm{\hslash }{\mathit{\omega }}_{\mathrm{0}}/{\mathit{\kappa }}_{B}T$, ω₀ is the nuclear Larmor frequency for the spins of interest and ${\widehat{I}}_{iz}$ is the z-angular momentum operator for spin i. The second term in Eq. (2) corresponds to longitudinal magnetization. However, outside of the high-temperature approximation higher-order terms in the spin density operator expansion cannot be ignored:

$$\begin{array}{}\text{(3)}& {\widehat{\mathit{\rho }}}_{\mathrm{eq}}\simeq \widehat{\mathrm{1}}+\mathbb{B}\sum _i{\widehat{I}}_{iz}+{\displaystyle \frac{{\mathbb{B}}^{\mathrm{2}}}{\mathrm{2}}}\sum _i\sum _j{\widehat{I}}_{iz}\cdot {\widehat{I}}_{jz}.\end{array}$$

The third term in Eq. (3) reveals the presence of nuclear dipolar order (Fukushima and Roeder, 1981), which can in principle be prepared by generating strongly polarized spin systems, such as those established by conducting dDNP experiments (Sugishita et al., 2019). Such dipolar order can also be efficiently generated by suitable rf-pulse sequences and ultimately used to transfer polarization (Jeener et al., 1965; Jeener and Broekaert, 1967; Redfield, 1969; Kunitomo et al., 1974; Demco et al., 1975; Emid et al., 1980; Vieth and Yannoni, 1993; Zhang et al., 1993; Kurur and Bodenhausen, 1995; Lee and Khitrin, 2008; Khitrin et al., 2011; Vinther et al., 2019). For the sake of simplicity, we will refer here to such polarization transfer schemes as dCP for dipolar order mediated cross-polarization.

In this article, we revisit the concept of ¹H→¹³C dCP polarization transfer and assess its efficiency in the context of dDNP experiments at 1.2 K and 7.05 T. We show that for a sample of [1-¹³C]sodium acetate, a ¹³C polarization of ∼8.7 % can be achieved after ∼10 min of ¹H DNP and the use of a sole polarization transfer step. The overall dCP transfer efficiency is ∼0.43 with respect to the most sophisticated and efficient high-power CP sequences available today. The experimental data presented indicate that ¹H Zeeman order (${\widehat{I}}_{\mathrm{z}}$) is first converted to ¹H–¹H dipolar order (${\widehat{I}}_{\mathrm{1}\mathrm{z}}\cdot {\widehat{I}}_{\mathrm{2}\mathrm{z}}$) and presumably subsequently converted to the desired ¹³C Zeeman order (${\widehat{S}}_{\mathrm{z}}$). We show how the use of microwave gating (Bornet et al., 2016b) is key to dCP as it improves the overall efficiency by a factor of more than ∼2.3.

2 Methods

2.1 Sample preparation and freezing

A solution of 3 M [1-¹³C]sodium acetate in the glass-forming mixture ${\mathrm{H}}_{\mathrm{2}}\mathrm{O}:{\mathrm{D}}_{\mathrm{2}}\mathrm{O}:\mathrm{glycerol}$-d₈ ($\mathrm{10}\mathit{\%}:\mathrm{30}\mathit{\%}:\mathrm{60}\mathit{\%}$ $v/v/w$) was doped with 50 mM TEMPOL radical (all compounds purchased from Sigma Aldrich) and sonicated for ∼10 min. This sample is referred to as I from here onwards. Paramagnetic TEMPOL radicals were chosen to most efficiently polarize ¹H spins under dDNP conditions. A 100 µL volume of I was pipetted into a Kel-F sample cup and inserted into a 7.05 T prototype Bruker Biospin polarizer equipped with a specialized dDNP probe and running TopSpin 3.7 software. The sample temperature was reduced to 1.2 K by submerging the sample in liquid helium and reducing the pressure of the variable temperature insert (VTI) towards ∼0.7 mbar.

2.2 Dynamic nuclear polarization

The sample was polarized by applying microwave irradiation at 197.648 GHz (positive lobe of the EPR line) with triangular frequency modulation of amplitude Δf_µw=120 MHz (Bornet et al., 2014a) and rate f_mod=0.5 kHz at a power of ca. 100 mW, which were optimized prior to commencing experiments to achieve the best possible level of ¹H polarization. Microwave gating was employed shortly before and during dDNP transfer experiments to allow the electron spin ensemble to return to a highly polarized state, which happens on the timescale of the longitudinal electron relaxation time (typically T_1e=100 ms with P_e=99.93 % under dDNP conditions) (Bornet et al., 2016b). Consequently, the ¹H and ¹³C relaxation times in the presence of a rf field are extended by orders of magnitude, allowing spin-locking rf pulses to be much longer, which significantly increases the efficiency of nuclear polarization transfer.

2.3 Pulse sequences

In 1967 Jeener and Broekaert established the original rf-pulse sequence for creating and observing dipolar order in the solid state (Jeener and Broekaert, 1967). Since then, other rf-pulse sequences have been proposed in the literature, usually with improved efficiency (Jeener et al., 1965; Redfield, 1969; Kunitomo et al., 1974; Demco et al., 1975; Emid et al., 1980; Vieth and Yannoni, 1993; Zhang et al., 1993; Kurur and Bodenhausen, 1995; Lee and Khitrin, 2008; Khitrin et al., 2011; Vinther et al., 2019). Herein, we are most interested in the rf-pulse sequence introduced by Vieth and Yannoni (Vieth and Yannoni, 1993) which is particularly simple, easily generates proton dipolar order and allows subsequent conversion to ¹³C polarization. Figure 1 shows this sequence adapted for our dDNP experiments. An electron-nuclear variant of this rf-pulse sequence has also been developed (Macho et al., 1991; Buntkowsky et al., 1991).

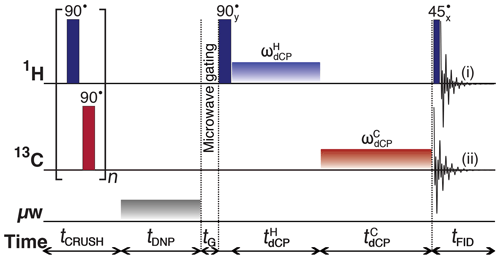
Figure 1 Schematic representation of the dCP rf-pulse sequence used for preparing and monitoring ¹H–¹H dipolar order in I, and the conversion to ¹³C transverse magnetization. The experiments used the following parameters, chosen to maximize magnetization-dipolar order interconversion: n=250; t_DNP=5 s; t_G=0.5 s; ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}/\mathrm{2}\mathit{\pi }=\mathrm{16.4}$ kHz; $t_{d\mathrm{CP}}^{\mathrm{H}}=\mathrm{25}$ µs; ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}/\mathrm{2}\mathit{\pi }=\mathrm{13.2}$ kHz; $t_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{39}$ ms. The ¹H and ¹³C continuous wave rf pulses have phase x. The π∕2 crusher rf pulses use a 13-step phase cycle to remove residual magnetization at the beginning of each experiment: $\mathit{\{}\mathrm{0},\mathit{\pi }/\mathrm{18}$, 5π∕18, π∕2, 4π∕9, 5π/18, 8π∕9, π, 10π∕9, 13π∕9, π∕18, 5π∕3, 35π∕18}. The resonance offset was placed at the centre of the ¹H and ¹³C NMR peaks.

The dCP rf-pulse sequence operates as follows:

• i.

  A crusher sequence of 90^∘ rf pulses with alternating phases separated by a short delay (typically 11 ms) repeated n times (typically n=250) kills residual magnetization on both rf channels.

• ii.

  The microwave source becomes active for a time t_DNP during which ¹H DNP builds up.

• iii.

  The microwave source is deactivated and a delay of duration t_G=0.5 s occurs before the next step, thus permitting the electron spins to relax to their highly polarized thermal equilibrium state (Bornet et al., 2016b).

• iv.

  A ¹H 90^∘ rf pulse followed by a π∕2 phase-shifted continuous wave ¹H rf pulse of amplitude ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}$ and length $t_{d\mathrm{CP}}^{\mathrm{H}}$ converts ¹H Zeeman polarization into ¹H–¹H dipolar order.

• v.

  A ¹³C square rf pulse of amplitude ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}$ and length $t_{d\mathrm{CP}}^{\mathrm{C}}$ presumably converts the ¹H–¹H dipolar order into ¹³C transverse magnetization.

The NMR signal can be detected by using either of the following: (i) a ¹H 45^∘ rf pulse followed by ¹H FID acquisition to monitor the remaining proton dipolar order; or (ii) ¹³C FID detection to observe the converted magnetization; see Fig. 1.

The dCP rf-pulse sequence can be used in several variants.

Variant no. 1: efficiency of ¹H–¹H dipolar order preparation.

• a.

  ¹H observation by fixing $t_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{0}$ ms and varying ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}$ and $t_{d\mathrm{CP}}^{\mathrm{H}}$ (Fig. 2a);

• b.

  ¹³C observation by fixing $t_{d\mathrm{CP}}^{\mathrm{C}}$ and ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}$ (typically to an optimal value) and varying ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}$ and $t_{d\mathrm{CP}}^{\mathrm{H}}$ (Fig. 2c).

Variant no. 2: efficiency of ¹H–¹H dipolar order conversion to ¹³C magnetization.

• a.

  ¹³C observation by fixing ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}$ and $t_{d\mathrm{CP}}^{\mathrm{H}}$ (typically to an optimal value) and varying ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}$ and $t_{d\mathrm{CP}}^{\mathrm{C}}$ (Fig. 3a);

• b.

  ¹H observation by fixing ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}$ and $t_{d\mathrm{CP}}^{\mathrm{H}}$ (typically to an optimal value) and varying ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}$ and $t_{d\mathrm{CP}}^{\mathrm{C}}$ (Fig. 4a).

The amplitudes of the ¹H and ¹³C dCP rf pulses (${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}$ and ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}$, respectively) were optimized iteratively until the intensity of the resulting NMR signals could not be improved further; see the Supplement for more details.

In the case of proton rf-channel acquisition, data points were acquired with a two-step phase cycle in which the phase of the 90_y rf pulse and the digitizer were simultaneously changed by 180^∘ in successive transients to remove spurious signals generated by longitudinal magnetization accrued during the dCP rf pulses. A dispersive lineshape was observed as a result of the phase cycle, which is characteristic of dipolar spin order. The resulting ¹H NMR spectrum was phase corrected to yield an absorptive lineshape.

3 Results

3.1 ¹H–¹H dipolar order preparation

¹H monitored optimization for the generation of ¹H–¹H dipolar order as a function of the dCP ¹H rf-pulse duration $t_{d\mathrm{CP}}^{\mathrm{H}}$ was performed by using variant no. 1a of the dCP sequence shown in Fig. 2a. Experimental results demonstrating the preparation of ¹H–¹H dipolar order under variant no. 1a of the dCP sequence are shown in Fig. 2b. The integrals plotted were acquired directly on the ¹H rf channel using ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}/\mathrm{2}\mathit{\pi }=\mathrm{16.4}$ kHz either with or without microwave gating (black circles and grey squares, respectively). In both cases, the NMR signal grows until a maximum signal intensity, which corresponds to the optimal preparation of proton dipolar order, is reached at $t_{d\mathrm{CP}}^{\mathrm{H}}\simeq \mathrm{25}$ µs, after which the signal decays towards a stable plateau on a longer timescale. However, in the case where microwave gating is removed, the signal intensity is reduced. This is due to depolarization (microwave saturation) of the electron spins, resulting in a detrimental enhancement of the paramagnetic relaxation contribution to nuclear spin relaxation. These results suggest that microwave gating improves the conversion of ¹H magnetization to ¹H–¹H dipolar order by a factor of at least ∼1.6.

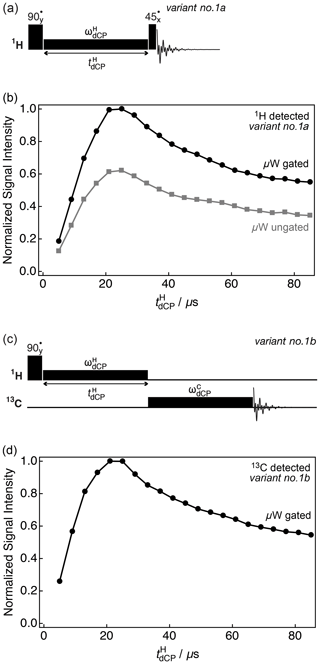
Figure 2 Simplified schematic representations of (a) variant no. 1a and (c) variant no. 1b of the dCP rf-pulse sequence. Experimental (b) ¹H and (d) ¹³C NMR signal intensities of I as a function of the ¹H dCP rf-pulse duration $t_{d\mathrm{CP}}^{\mathrm{H}}$ acquired at 7.05 T (¹H nuclear Larmor frequency =300.13 MHz, ¹³C nuclear Larmor frequency =75.47 MHz) and 1.2 K. The experiments in (b) were acquired with two transients per data point, whilst the experiments in (d) were acquired with a single transient per data point. The traces have the same overall form and plateau over a period of 200 µs (data not shown).

¹³C-monitored optimization for the build-up of ¹H–¹H dipolar order was performed by using variant no. 1b of the dCP rf-pulse sequence demonstrated in Fig. 2c. In Fig. 2d the experimental integrals are plotted against the dCP ¹H rf-pulse duration $t_{d\mathrm{CP}}^{\mathrm{H}}$ and were acquired on the ¹³C rf channel with ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}/\mathrm{2}\mathit{\pi }=\mathrm{16.4}$ kHz, ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}/\mathrm{2}\mathit{\pi }=\mathrm{13.2}$ kHz and $t_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{39}$ ms (black circles). It is important to note that the maximum is identical whether the NMR signal is observed on the ¹H rf channel by using variant no. 1a or on the ¹³C rf channel by using variant no. 1b, and that more generally the two traces have the same shape and optimum. This shows that ¹³C transverse magnetization from dCP is proportional to the ¹H–¹H dipolar order initially prepared.

3.2 ¹H–¹³C polarization transfer

Figure 3b shows how ¹³C magnetization is built up by employing variant no. 2a of the dCP rf-pulse sequence; see Fig. 3a. The experimental integrals of the ¹³C signal are plotted against the ¹³C dCP rf-pulse duration $t_{d\mathrm{CP}}^{\mathrm{C}}$ with (black circles) and without (grey squares) microwave gating.

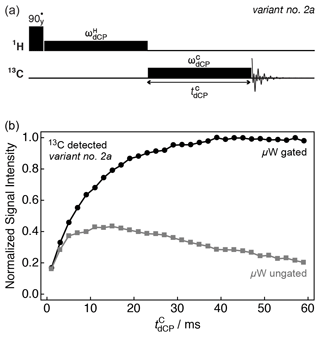
Figure 3 (a) Simplified schematic representation of variant no. 2a of the dCP rf-pulse sequence. (b) Experimental ¹³C NMR signal intensity of I as a function of the dCP rf-pulse duration $t_{d\mathrm{CP}}^{\mathrm{C}}$ acquired at 7.05 T (¹H nuclear Larmor frequency =300.13 MHz; ¹³C nuclear Larmor frequency =75.47 MHz) and 1.2 K with a single transient per data point.

The black trace corresponds to the growth of the ¹³C NMR signal. A maximum is reached at $t_{d\mathrm{CP}}^{\mathrm{C}}\simeq \mathrm{39}$ ms, with ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{13.2}$ kHz. The polarization transfer efficiency is relatively robust with respect to the amplitude of the ¹³C dCP rf-pulse ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}$; see the Supplement for more details. A wildly different behaviour is observed in the case where the microwave source is not gated. In this instance, a maximum signal intensity occurs at $t_{d\mathrm{CP}}^{\mathrm{C}}\simeq \mathrm{15}$ ms, with the detectable ¹³C signal decreasing past this point. The ratio between the maximum data points is ∼2.3, and indicates a large ¹³C enhancement afforded by microwave gating.

It is worth noting that the duration of the ¹³C dCP rf-pulse is considerably longer, more than 3 orders of magnitude, than the ¹H dCP rf-pulse length. Reasons for this are examined in the discussion section below.

Figure 4b details how in variant no. 2b of the dCP rf-pulse sequence (Fig. 4a) the ¹H NMR signal vanishes as the ¹³C dCP rf-pulse generates ¹³C transverse magnetization. The experimental integrals of the ¹H-detected NMR signals are plotted against the ¹³C dCP rf-pulse duration $t_{d\mathrm{CP}}^{\mathrm{C}}$ with ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{0}$ (black open circles) and ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{13.2}$ kHz (black circles) both with microwave gating, and with ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{13.2}$ kHz (grey squares) without microwave gating.

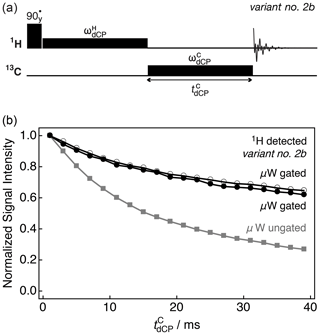
Figure 4 (a) Simplified schematic representation of variant no. 2b of the dCP rf-pulse sequence. (b) Experimental ¹H NMR signal intensity of I as a function of the ¹³C dCP rf-pulse duration $t_{d\mathrm{CP}}^{\mathrm{C}}$ acquired at 7.05 T (¹H nuclear Larmor frequency =300.13 MHz; ¹³C nuclear Larmor frequency =75.47 MHz) and 1.2 K with two transients per data point. The experimental traces were recorded by using the following amplitudes for the ¹³C dCP rf-pulse ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}$: black open circles: ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{0}$ kHz; black filled circles: ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{13.2}$ kHz; grey squares: ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{C}}=\mathrm{13.2}$ kHz. All signal amplitudes were normalized to the first data point.

The curves show how ¹H–¹H dipolar order decays towards thermal equilibrium mainly through relaxation and is not significantly affected by the presence of the ¹³C dCP rf-pulse generating ¹³C magnetization. The difference between the two black traces might however indicate the quantity of ¹H–¹H dipolar order converted into ¹³C magnetization. The small difference is just a few percent, indicating that only a very small portion of the ¹H–¹H dipolar order might be used (and be useful) to produce hyperpolarized ¹³C magnetization. This could be explained by the large excess of ¹H spins compared with ¹³C spins in our sample (a factor of ∼6.2). A lack of microwave gating (grey squares) significantly compromises the generation of ¹³C polarization, as seen in Fig. 3b.

3.3 Comparison to cross-polarization

The performance efficiency of the dCP rf-pulse sequence was compared to a traditional CP experiment (Hartmann and Hahn, 1962; Pines et al., 1972; Perez Linde, 2009; Jannin et al., 2011; Bornet et al., 2012, 2013; Batel et al., 2012; Vuichoud et al., 2016; Cavaillès et al., 2018), which is described in the Supplement along with a rf-pulse sequence diagram and all optimized parameters. Experiments employed 640 s of direct ¹H DNP at 1.2 K prior to polarization transfer to the ¹³C heteronucleus.

The power requirements for polarization transfer are dependent upon the rf-pulse sequence used and the capabilities of the dDNP probe. In general, the peak power for the ¹³C dCP rf-pulse is ∼5.4 times lower than required for CP. However, the ¹³C dCP rf-pulse is active for a duration ∼5.6 times longer than that of CP, and hence the overall deposited rf-pulse energy is approximately the same for both rf-pulse sequences. Notwithstanding, the moderately lower ¹³C dCP rf-pulse power is highly advantageous, e.g. a decreased likelihood of probe arcing events within the superfluid helium bath. The benefit of employing the dCP rf-pulse sequence becomes even more apparent when examining the proton rf-pulse durations needed for ¹H–¹³C polarization transfer. Although the peak powers of both rf-pulse sequences are similar, the duration of the ¹H dCP rf-pulse is a factor of 280 times shorter than that recommended for adequate CP. This is advantageous in the case that the B₁ field produced by the dDNP probe is weak (e.g. due to large sample constraints) or is unstable at higher ¹H rf-pulse powers for sufficiently long durations.

The CP rf-pulse sequence achieved a ¹³C polarization level of P(¹³C) ≃20.4 % after a single CP contact. ¹³C polarization levels in excess of 60 % are anticipated by using a multiple CP contact approach (Perez Linde, 2009; Jannin et al., 2011; Bornet et al., 2012, 2013; Batel et al., 2012; Vuichoud et al., 2016; Cavaillès et al., 2018). In comparison, the integral of the dCP-filtered NMR signal maximum is scaled by a factor of ∼0.43, indicating a ¹³C polarization of P(¹³C) ≃8.7 %. This is consistent with previous results reported in the literature (Perez Linde, 2009; Vinther et al., 2019). Strategies to further improve the dCP efficiency are presented in the discussion section.

4 Discussion

The results presented in Fig. 2b and d show how the achieved ¹³C polarization is directly proportional to the quantity of ¹H–¹H dipolar order initially prepared by the ¹H dCP rf-pulse. However, even if the ¹³C polarization closely follows the shape of the proton dipolar order creation profile, this does not constitute irrefutable proof that the ¹³C polarization originates from the proton dipolar order reservoir itself. Other, more complex forms of nuclear spin order might be involved. Moreover, it is feasible that an intermediate reservoir exists, such as non-Zeeman spin order of the ¹³C heteronucleus.

As seen in Fig. 3b, it is interesting to note that the duration of the ¹³C dCP rf-pulse is considerably longer, more than 3 orders of magnitude, than the ¹H dCP rf-pulse duration. The reason is the relative sizes of the dipolar couplings which control the preparation and transfer processes of ¹H–¹H dipolar order. The generation of dipolar order involves only proton spins, which possess a magnetogyric ratio ∼4 times greater than for ¹³C spins and consequently larger dipolar couplings, which scale as the product of the magnetogyric ratios for the two spins involved. This results in a short time to convert ¹H magnetization to ¹H–¹H dipolar order. Conversely, the supposed transfer of ¹H–¹H dipolar order to ¹³C nuclei would certainly demand ¹H–¹³C dipolar couplings.

The duration of the ¹³C dCP rf-pulse is a factor of ∼5.6 longer than required for optimized conventional CP (see the Supplement for more details). The extended duration of the ¹³C dCP rf-pulse could be conceivably explained by assuming that the ¹H spins closest to the ¹³C spin do not participate in the polarization transfer process since the ¹H–¹H dipolar order preparation is perturbed by the presence of the ¹³C spin during the ¹H dCP rf-pulse. It is also possible that two dipolar coupled protons are separated by a difference in chemical shift which matches the frequency of a ¹³C spin in the rotating frame allowing an exchange of energy. Such events are similar to the cross-effect in DNP (Kessenikh et al., 1963), but are likely to be of lower probability, leading to an increased ¹³C dCP rf-pulse duration.

Not only is the polarization transfer process long, but it is also weaker than what is usually realized with optimized CP, since we obtain P(¹³C) ≃8.7 % rather than P(¹³C) ≃20.4 % in a single CP step on the same sample. Although the amplitude ${\mathit{\omega }}_{d\mathrm{CP}}^{\mathrm{H}}$ and duration $t_{d\mathrm{CP}}^{\mathrm{H}}$ of the proton dipolar order creation rf-pulse were carefully optimized before experimental implementation, we nevertheless believe there is still room for improvement in preparing high quantities of proton dipolar order. The performance of the dCP rf-pulse sequence could be enhanced by adopting the following strategies: (i) employing shaped rf-pulses; (ii) implementing a multiple dCP transfer approach; (iii) optimizing the protonation level of the DNP solution; (iv) exploiting deuterated molecular derivatives; (v) avoiding large quantities of methyl groups which may act as dipolar order relaxation sinks due to their inherent rotation (which remains present at liquid helium temperature); and (vi) changing the molecule [1-¹³C]sodium acetate for another spin system with different ¹H–¹³C coupling strengths (e.g. simply using [2-¹³C]sodium acetate).

Today's performances on our current “standard” DNP sample are rather poor compared to CP; however, there are reasons to think that further improvements through advanced rf-pulse schemes and revised sample formulations will be possible in the future, and that dCP may become a viable alternative to CP. This will be particularly relevant to the cases of the following: (i) issues related to probe arcing in the superfluid helium bath which precludes the use of conventional CP experiments; (ii) increased sample volumes, e.g. in human applications; and (iii) hyperpolarization of insensitive nuclear spins: e.g. ⁸⁹Y nuclei cannot be polarized easily via traditional CP experiments due to unfeasible CP matching conditions on the heteronuclear rf channel. Other alternatives to the CP approach also exist but are theoretically less efficient, such as low magnetic field nuclear thermal-mixing (Gadian et al., 2012) which relies on energy conserving mutual spin flips in overlapping NMR lineshapes to polarize heteronuclei in solid samples (Peat et al., 2016).

5 Conclusions

Dipolar order mediated ¹H→¹³C polarization transfer occurs by employing rf-pulse methods which operate under dDNP conditions. This supposedly involves an intermediate reservoir of dipolar order, which governs the polarization transfer process. The spin dynamics of dCP were found to significantly depend on the presence of microwave gating. A maximum ¹³C polarization of ∼8.7 % was observed after ∼10 min of microwave irradiation and a lone polarization transfer step, which corresponds to a dCP polarization transfer efficiency of ∼0.43 with respect to optimized conventional CP. These results are promising for future applications of polarization conversion methods in the context of low-power ¹H→X polarization transfer to insensitive nuclei (in particular for very low magnetogyric ratios), with minimized probe arcing and potentially large sample volumes, paving the way to the use of ¹H→X polarization transfer in clinical (human-dose) contexts and for nuclear spins generally less accessible by dDNP such as ¹⁵N or ⁸⁹Y.