EPR study of NO radicals encased in modified open C₆₀ fullerenes

Using pulsed electron paramagnetic resonance (EPR) techniques, the low-temperature magnetic properties of the NO radical being confined in two different modified open C₆₀-derived cages are determined. It is found that the smallest principal g value g₃, being assigned to the axis of the radical, deviates strongly from the free electron value. This behaviour results from partial compensation of the spin and orbital contributions to the g₃ value. The measured g₃ values in the range of 0.7 yield information about the deviation of the locking potential for the encaged NO from axial symmetry. The estimated 17 meV asymmetry is quite small compared to the situation found for the same radical in polycrystalline or amorphous matrices ranging from 300 to 500 meV. The analysis of the temperature dependence of spin relaxation times resulted in an activation temperature of about 3 K, assigned to temperature-activated motion of the NO within the modified open C₆₀-derived cages with coupled rotational and translational degrees of freedom in a complicated three-dimensional locking potential.

1 Introduction

In a series of recent publications, the Kyoto Group has shown that it is possible to encapsulate small and even reactive molecules in a modified C₆₀ cage with tailored entrance and exit holes (Hasegawa et al., 2018a; Futagoishi et al., 2017; Hashikawa et al., 2018). Using such designer-type open cages instead of closed structures creates a new route for the preparation of interesting compounds. The family of endohedral fullerenes with closed carbon cages like N@C₆₀ (Murphy et al., 1996), He@C₆₀ (Saunders et al., 1994), H₂@C₆₀ (Komatsu et al., 2005), H₂O@C₆₀ (Kurotobi and Murata, 2011), HF@C₆₀ (Krachmalnicoff et al., 2016), and CH₄@C₆₀ (Bloodworth et al., 2019), as well as C₈₂ (Stevenson et al., 1999) based metallo-endohedrals, can thus be expanded significantly. It has been shown that these new compounds can be stable under ambient conditions, allowing easy handling. If encapsulated molecules are paramagnetic, as in the case of ³O₂ or ²NO, electron paramagnetic resonance (EPR) is the method of choice for elucidating their properties. This not only allows determination of the stationary-spin Hamilton parameters, but furthermore allows detection of dynamic properties arising from internal dynamics or motion of the compound as a whole. In the case of La@C₈₂ for instance, it was possible to conclude from an analysis of two-dimensional EXCSY spectra that the metal ion is rigidly locked to the inside surface of the carbon cage (Rübsam et al., 1996). In the present case of an encapsulated NO radical it was concluded from the broad variance of its principal g matrix values (Hasegawa et al., 2018a) that even at low temperatures the radical is not fixed to a particular site. It was remarkable that the very small value quoted for the axial component (Hasegawa et al., 2018a) of 0.225 deviates significantly from the value determined for NO radicals trapped in a single crystal host (Ryzhkov and Toscano, 2005) or NO radicals adsorbed in zeolites (Poeppl et al., 2000). This very small value of g₃=0.225, deduced by an analysis of a continuous wave (cw) measurement, necessitated confirmation by pulse EPR experiments, better suited for the study of very broad spectra. Although a T₂ variation as a function of the external field can distort the shape of a pulse-derived spectrum to some extent, difficulties in detecting extremely broad spectra with virtually absent changes within the typically achievable B₀ modulation amplitudes in cw EPR can lead to misinterpretations, in particular if the supposed spectrum extends a factor of 2 beyond the possible acquisition range. So far, neither relaxation nor nitrogen hyperfine data were reported, which might be important for a full characterization of the compound. It was the aim of the present study to obtain by multi-frequency EPR and ENDOR techniques a complete spin Hamiltonian parameter set for the encapsulated radical. In addition, the anticipated effects of a non-spherical cage potential on the radical are explored, and effects due to the structural modification of the cage are studied.

2 Experimental part

2.1 Sample preparation

NO radicals trapped in two slightly different modified C₆₀ cages, C₈₂H₂₈N₃O₅S and C₈₂H₃₂N₃O₅S, were studied, in the following abbreviated by NO@C60-OH1 and NO@C60-OH3, respectively (see Fig. 1 for NO@C60-OH1 and Fig. A1 for NO@C60-OH3). The notation indicates the two different orifices with one and three OH groups, respectively. NO@C60-OH1 was prepared as described in Hasegawa et al. (2018a) and NO@C60-OH3 combining the procedures described in Hashikawa et al. (2018) and Hasegawa et al. (2018a). NO@C60-OH1 and NO@C60-OH3 were dissolved in CS₂ in 2.5 and 10 mM concentrations and sealed in quartz tubes for EPR spectroscopy.

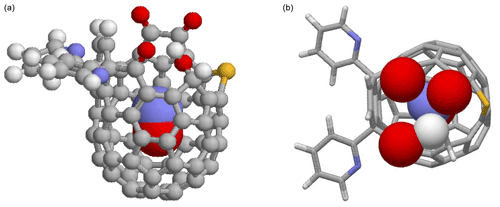
Figure 1 DFT-optimized structure of NO@C60-OH1 with N “up”. (a) Ball-and-stick representation of the modified C₆₀ cage and van der Waals spheres of the caged NO with carbon (grey), hydrogen (white), nitrogen (blue), oxygen (red), and sulfur (yellow). (b) Top view on the orifice with stick representation of the cage except van der Waals spheres for the oxygen and hydrogen atoms of the orifice and the caged NO.

2.2 EPR spectroscopy

For pulsed EPR and ENDOR measurements at S- and X-band mw frequencies (3.4 and 9.8 GHz), various setups were employed. Echo-detected 9.8 GHz EPR measurements at low temperatures were conducted on Bruker ElexSys E580 and E680 instruments equipped with Oxford CF935 helium cryostats using Bruker MD4 Flexline ENDOR probe heads. Field-swept echo-detected EPR spectra (FSE) at 9.8 GHz were recorded using a two-pulse “Hahn-echo” sequence (20–300–40 ns) at temperatures of 3.6 to 12 K, yielding absorption-type spectra. Transient nutation measurements at 9.8 GHz were conducted by applying a PEANUT (Stoll et al., 1998) pulse sequence with a π∕2 pulse length of 8 ns, a delay time τ of 130 ns and a high turning angle (HTAx) pulse of 4096 ns. Phase inversion time within the high turning angle (HTAx) pulse was incremented by 2 ns starting with an initial inversion after 16 ns. ENDOR spectra were recorded by applying either a Mims pulse sequence with π∕2 pulses of 20 ns, a delay time τ of 200 ns and a rf π pulse length of 15 µs, or a Davies pulse sequence with pulse settings 40–30 000–20–200 ns and a RF pulse length of 25 µs. FSE data at a microwave frequency of 3.4 GHz (S-band) were obtained again using a Bruker ElexSys E680 system with an additional S-band accessory including a Bruker Flexline probe head with a split-ring resonator employing a pulse timing of 32–500–64 ns. FSE and ENDOR spectra were fitted by the EasySpin (Stoll and Schweiger, 2006) “esfit” routine using the “pepper” and “salt” simulation routines.

2.3 Quantum chemical calculations

Optimization of the structure of the compounds NO@C60-OH1 and NO@C60-OH3, with replacement of the 6-t-Butylpyridin-2-yl groups with 2-pyridyl groups, has been performed using Gaussian (Frisch et al., 2016) at the HPC center of FU Berlin. DFT calculations were performed using the 6-311++ basis set with UB3LYP exchange. Structures derived for nitrogen in the “up” orientation (with respect to the orifice) are depicted in Figs. 1 and A1. The difference in total energies for “up” and “down” orientations of the trapped radical was 22.6 meV for NO@C60-OH1, somewhat larger than the value (8 meV) published earlier (Hasegawa et al., 2018a), which might be caused by use of a different basis set. For NO@C60-OH3 we calculated 40.2 meV.

3 Results and discussion

3.1 Multi-frequency EPR data

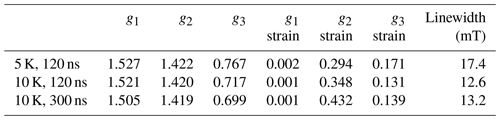
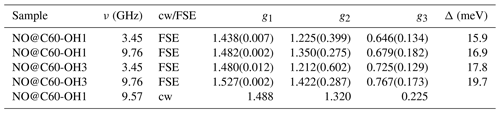
EPR data published previously by Hasegawa et al. (2018a) for NO@C60-OH1 were obtained in cw mode at a microwave frequency of 9.56 GHz. Spectra measured at 3.45 and 9.76 GHz using the FSE technique are depicted in Fig. 2. The published g matrix parameter set (see Table 1) obtained by spectral simulation of the cw spectrum is characterized by an extreme g anisotropy. The values determined by fitting the FSE spectra confirm the two larger g matrix parameters; however, they deviate significantly with respect to the pseudo-axial g₃ parameter.

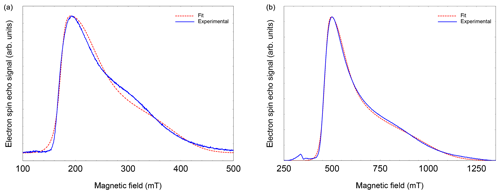
Figure 2 FSE spectra of NO@C60-OH1 (T=5 K) with best fits. (a) S-band (3.5 GHz, 10 mM/CS₂). (b) X-band (9.7 GHz, 2.5 mM/CS₂). For fitting a set of nitrogen hyperfine tensor parameters was used, determined by ENDOR (see below).

Table 1 Fit-determined g matrix data of both compounds (gStrain fit parameters are listed in brackets). Previously published values (Hasegawa et al., 2018a) are given for comparison. Level splittings Δ deduced from the deviation of the pseudo-axial g₃ parameter from g_e are also shown.

We quote no error margins, because a large g strain value is obtained for the g₃ value using the “esfit” routine (EasySpin; Stoll and Schweiger, 2006). The pseudo-axial principal parameters g₃=0.646 and 0.679, respectively, are still found to be very small compared to g₃=1.7175 for the same compound trapped in a crystal (Ryzhkov and Toscano, 2005) or g₃=1.888 when incorporated into a zeolite (Poeppl et al., 2000), but rendering the g matrix substantially less anisotropic compared to the data in Hasegawa et al. (2018a). For further confirmation of the g matrix parameter set determined by fitting the FSE spectra, we also performed a PEANUT experiment (Stoll et al., 1998), probing the Rabi nutation frequency as a function of B₀ (see below).

Parameters determined for the NO@C60-OH3 compound are also listed in Table 1. Spectra are shown in Fig. A2 in Appendix A. Also for this compound with a slightly modified cage a similar set is observed, the fit parameters changing slightly towards larger values compared to those found for the OH1 compound. Even the slight difference in cage structure apparently is influencing the g matrix values. However, no prominent features of anticipated magnetic interaction between encapsulated NO radicals within the intermolecular hydrogen-bonded dimeric triply hydroxylated C₆₀-derived cages were observed.

Because of the rather large deviation of the g_i parameters from the free electron value and the large anisotropy of g, a significant variation of the nutation frequency was expected as a function of orientation. If by orientation selection a particular g principal position is chosen, the two remaining g parameters determine the nutation frequency. As shown in Fig. 3, all Rabi frequencies are smaller than the reference value determined by a standard coal sample and increase towards the high field spectral range. In Fig. 3, the expected nutation frequency distributions (Stoll et al., 1998) are indicated by dashed vertical lines at the g principle values using the values for NO@C60-OH3 at X-band in Table 1. The agreement is quite convincing, and a very small g₃ parameter as deduced earlier can be excluded, since it would lead to much smaller nutation frequencies down to ≈3.7 MHz in the perpendicular orientations (g₁ and g₂ region, 500 mT region) of the radical. Thus, the small value of g₃=0.225 (Hasegawa et al., 2018a) is probably caused by overestimating the flat high field part of the cw spectrum in the simulation.

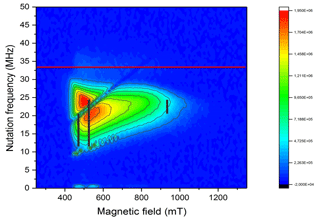
Figure 3 PEANUT spectrum of NO@C60-OH3 measured at 5 K. The red line indicates the reference frequency measured for a coal sample with isotropic g=2. The black vertical lines indicate the expected nutation frequency distributions (Stoll et al., 1998) at the three principal g values for NO@C60-OH3 in Table 1 (X-band).

It should be noted that the g matrix parameters of the encapsulated NO radical deviate much more from the free electron value g_e=2.0023 compared to data reported for situations when the radical is either trapped in a crystal [$\mathbf{g}=\left(\mathrm{1.9740}\right(\mathrm{7}),\mathrm{1.9766}(\mathrm{7}),\mathrm{1.7175}(\mathrm{4}\left)\right)$] (Ryzhkov and Toscano, 2005), adsorbed at the surface of metal oxides [$\mathbf{g}=(\mathrm{1.97},\mathrm{1.97},\mathrm{1.91})$] (Lunsford, 1968), or incorporated into a zeolite [$\mathbf{g}=(\mathrm{2.001},\mathrm{1.996},\mathrm{1.888})$] (Poeppl et al., 2000). This clearly indicates that the orbital momentum of the radical is much less quenched in the C₆₀-derived cages. Following the idea that partial quenching of the orbital angular momentum is caused by lifting of the degeneracy between the antibonding ²π_x and ²π_y orbitals, the energy splitting Δ between these orbitals can be estimated by the pseudo-axial value of the NO g matrix (Ryzhkov and Toscano, 2005; Lunsford, 1968):

$$\begin{array}{}\text{(1)}& g_{\mathrm{3}}=g_{\mathrm{e}}-\mathrm{2}\mathit{\lambda }L/({\mathit{\lambda }}^{\mathrm{2}}+{\mathrm{\Delta }}^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

Here, λ is the spin-orbit coupling constant (123.16 cm⁻¹ for NO; James and Thibault, 1964), Δ defines the crystal-field splitting of the ²π_x and ²π_y orbitals, and L is a correction to the angular momentum along z caused by the crystal field. L is equal to 1 for a free molecule. A change in L represents a modification of the molecular wave function by the crystal field. It should be noted, however, that in previous studies (Zeller and Känzig, 1967; Shuey and Zeller, 1967) no significant deviations from 1 were observed. The highly nonlinear dependence of g₃ on Δ is depicted in Fig. A3 (Appendix A). Using Eq. (1), a level splitting of approximately 17 meV (200 K) is determined from g₃≈0.7 for NO@C60-OH1 and 20 meV from g₃≈0.8 for NO@C60-OH3 (see Table 1).

The lifting of the ²π_x∕²π_y degeneracy is not unexpected considering the observation of a finite zero-field splitting (ZFS) for ³O₂ in a cage with C₁ symmetry (Futagoishi et al., 2017). In this study the potential barrier for librational motions of ³O₂ was estimated as 398 cm⁻¹ (49 meV) by measuring the shift of its principal ZFS component with respect to the value of the free molecule. The size of this potential barrier is on the same order of magnitude as the one calculated here for NO. The lifting of degeneracy leads to a deviation of the orbitals from two fully circular symmetric angular momentum eigenstates with opposite momentum to two orthogonal elliptic orbitals not being angular momentum eigenstates, but with non-vanishing angular momentum expectation values. With a 200 K level splitting only one of the orbitals is occupied at 5 K and rotation of the molecule corresponds to transitions from one to the other eigenstate, which should be impossible due to the large level splitting. Nevertheless, the remaining angular momentum expectation value gives rise to the very small g₃ value. The splitting is much less than values found for ²NO and ${}^{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}^{-}$ trapped in crystals, on surfaces, or in zeolites, which range from 300 to 500 meV.

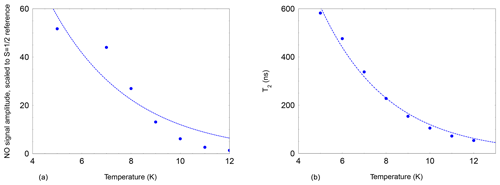
Figure 4 Echo-detected signal of NO@C60-OH3 (480 mT, 9.7 GHz, 2.5 mM/CS₂, 200 ns pulse separation) as a function of temperature. The signal intensity is scaled to the intensity of a field-separated g≈g_e signal from an unidentified $S=\mathrm{1}/\mathrm{2}$ species following the Curie law. An exponential temperature dependence is assumed for the fit (dashed line) with a decay constant of 3 K. (b) Temperature dependence of the spin echo decay constant T₂ of NO@C60-OH3 (480 mT, 9.7 GHz, 2.5 mM/CS₂). The faster decay constant with larger weight is shown in cases where the time traces required a bi-exponential fit. Again an exponential temperature dependence is assumed for the dashed line, with a decay constant of 3.1 K.

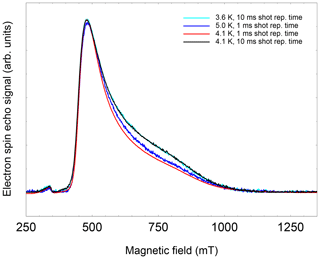
The ²π_x and ²π_y level splitting is of the same order of magnitude as the energy difference for the “up” and “down” orientation of the NO radical with respect to the cage opening calculated earlier (Hasegawa et al., 2018a) and also found in this study. For “up”/“down” axis reorientation a factor 10 larger barrier was found. Considering the additional degree of freedom of hindered rotation about the axis of the radical with an unknown transition barrier, this gives rise to a complicated three-dimensional orthorhombic potential energy surface. It is not surprising that under these conditions the EPR signal can be detected only at very low temperatures. The temperature dependence of the NO FSE signal (X-band) was measured relative to an unidentified stable $S=\mathrm{1}/\mathrm{2},g\approx g_{\mathrm{e}}$ species in the sample and is shown in Fig. 4 (left). The NO signal decreases much faster upon temperature increase than according to the Curie law since a dramatic signal loss relative to the reference signal is observed. This strong additional signal decay of the NO radical beyond the Curie law can be described by an activation temperature of about 3 K.

The dramatic loss of signal intensity by a factor 50 in the narrow temperature range of 5 to 12 K is indicative of a decrease in T₂. This was confirmed by measuring the two-pulse echo decay constant $T_{\mathrm{2}}^{\ast }$ at the peak signal position. Its temperature dependence could be fitted assuming exponential temperature dependence with an activation temperature of 3.1 K as shown in Fig. 4 (right).

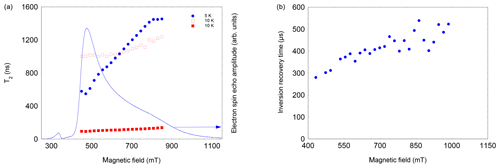
Figure 5 (a) Field and temperature dependence of the two-pulse echo decay of NO@C60-OH3. The 5 K data set could be satisfactorily fitted assuming a single exponential; the 10 K data required a bi-exponential fit. Both components were of similar magnitude, with the shorter T₂ larger in amplitude. (b) Field dependence of T₁ of NO@C60-OH3, measured using an inversion recovery pulse sequence at 3.6 K.

Measuring the field dependence of $T_{\mathrm{2}}^{\ast }$ at different temperatures supports the simple model of a restricted rotation. As shown in Fig. 5 left, at 5 K the $T_{\mathrm{2}}^{\ast }$ values increase from 600 to 1500 ns, with probing radicals changing from perpendicular to parallel orientation. This can be taken as evidence that small angle librations around the long axis are activated at this temperature, whereas long-axis reorientations are still prevented at this temperature. In contrast, at 10 K this restriction is no longer valid, shortening the echo decay accordingly for the full field range; i.e. librations about all molecular axes occur.

This hypothesis is also supported by the observation that T₁, determined by inversion recovery, also increases significantly at T=3.6 K when moving from perpendicular to parallel orientation (see Fig. 5, right). This field dependence of T₁ leads even at 3.6 K to a noticeable change in the FSE pattern if the pulse repetition time is not sufficiently long (see Fig. A4, Appendix A). While T₁ and T₂ show a significant temperature dependence, the spectral shape, and thus the g parameters, are virtually unaffected within the temperature range of 3.6 to 12.5 K (see Table B1, Appendix B).

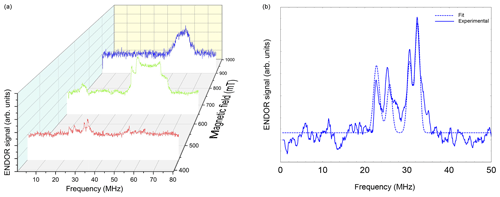
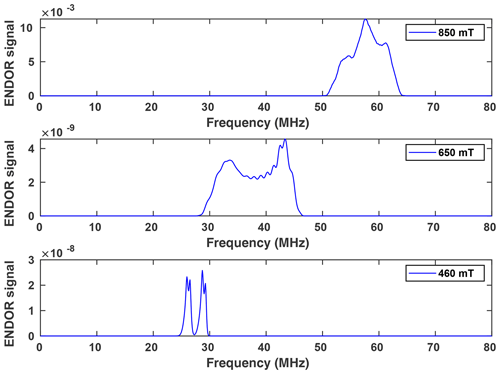
Figure 6 (a) Davies ENDOR spectra of NO@C60-OH1 (T=5 K, 10 mM/CS₂) measured as a function of B₀. Spectra are corrected with respect to different accumulation times for better comparison of spectral patterns. The Davies ENDOR pulse sequence (40–30 000–20–200–40 ns, 25 µs rf pulse) was identical for all spectra. (b) ENDOR spectrum of NO@C60-OH1 measured at 440 mT (see panel a) together with simulation.

Loss of the cw EPR signal intensity at temperatures above 80 K was also reported in Hasegawa et al. (2018b). Since the cw signal intensity is not affected by $T_{\mathrm{2}}^{\ast }$, the NO signal could be detected in cw mode up to 40 K (Hasegawa et al., 2018b), with a much smaller decrease from 5 to 20 K than observed in our pulsed EPR study probing the echo signal with a two-pulse sequence. The low activation temperature of 3 K (∼0.3 meV) has to be compared to the much larger values found in the case of N@C₆₀ and P@C₆₀, in which a well-defined potential of spherical or axial symmetry leads to degenerate vibrational levels of the translational degree of freedom of encapsulated atoms in the range of 8 to 16 meV (Pietzak et al., 2002), respectively. The partially opened cage resembles more the situation in the C₇₀ cage by providing a nearly axial potential. Assuming that vibration along this preferred axis is lowest in energy and taking into account the larger mass of the radical, a vibrational eigenfrequency of about 5 meV for the center of mass (CM) of the radical would be expected, which is still more than 1 order of magnitude larger than the experimental value. In contrast to encapsulated atoms, we also have to consider for the NO case a librational mode of the radical with respect to the cage axis. In a study of H₂ encapsulated in C₆₀ or C₇₀, the eigenstates of H₂ were determined numerically by invoking the appropriate five-dimensional potential surface, describing translational and rotational degrees of freedom (Xu et al., 2009; Mamone et al., 2013). Lacking numerical values for the potential surface in our more complicated case, it is only possible to estimate typical values for the librational mode by approximating the interconversion between “up”/“down” (its z axis) of the radical axis in a potential well of 80 meV (645 cm⁻¹) (Hasegawa et al., 2018a) as a torsional oscillator. Converting the 80 meV rotational barrier into a torsion spring constant for librations of κ=40 meV and using $\mathit{\omega }=\sqrt{\mathit{\kappa }/\mathit{\theta }}$ with the moment of inertia θ of NO, we arrive at a characteristic mode energy for the libration of about 4 meV (about 40 K), which is substantially larger than the experimentally observed activation temperature. However, when including transverse degrees of freedom for axis reorientation, it is not unlikely that the characteristic mode energies might further be reduced towards the experimental value.

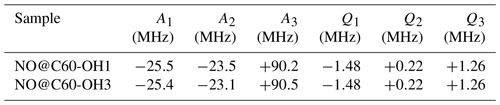
Table 2 Hyperfine parameters determined by fitting Davies ENDOR spectra measured under orientation selection conditions providing the best resolution. For an assignment of signs, see text. n.d.: not determined.

Table 3 Hyperfine parameters calculated for NO@C60-OH1 and NO@C60-OH3 in their “up” configuration using Gaussian G16/A03 (G16/A03, B3LYP, 6-311++). The calculated values for the “down” orientation differ by less than 3 %.

3.2 ENDOR data

Orientation-selective ENDOR spectra of NO@C60-OH1 were measured at 9.7 GHz. As depicted in Fig. 6 (left), the center of lines shifts towards higher frequency when changing the observation field position from the lowest to highest edges of the absorption pattern. The frequency position at the low field side of the spectrum and the magnitude of the shift is inconsistent with proton hfi but is indicative of a dominant dipolar ¹⁴N hfi, allowing simple determination of A_i for the extreme field positions. For a determination of dipolar and quadrupolar hfi parameters, observation field values at the low and high ends of the FSE spectrum were chosen, anticipating that g matrix and hfi tensor axes are collinear. Best ENDOR resolution is obtained at the low field edge, allowing determination of some hfi parameters by fitting, as shown in Fig. 6 (right).

At this field position a consistent fit is obtained by only fixing the nuclear Larmor frequency to its field-determined value. At the high field edge no line quartet is observed for this compound. The broad pattern, however, is consistent with the result of a spectral simulation, shown in Fig. 7, using a parameter set completed with the nqi parameter of NO@C60-OH3, being better resolved at the high-field edge of the ENDOR pattern. It should be noted that no simple pattern is expected for the intermediate field range because of significant g strain. For this reason fit values are only quoted assigned to the g₁ and g₃ axis directions. No information about the signs of hfi parameters can be deduced from the experimental spectra. The assignments given in Table 2 are tentatively made by invoking the calculated hfi constants (see Table 3). Although not in very good quantitative agreement with the experiment, the calculated small isotropic hfi (+15 MHz) necessitates assignment of a negative sign to A₁. Lacking spectral resolution when probing at the high field edge due to the large g₃ strain, the center of gravity still gives a reliable value for the large dipolar hfi for both compounds. The absent spectral resolution, even when observing at the van Hove singularities of the FSE spectrum, could result from a simultaneous presence of “up”/“down” configurations as observed in X-ray crystallography, with slightly different hfi parameters.

Figure 7 Simulated ENDOR spectra of NO@C60-OH1, using parameters listed in Table 2.

4 Conclusions

Using various EPR techniques, the spin Hamiltonian parameters for the encapsulated NO radical are determined. The radical, being confined in C₆₀-derived cages, exemplifies the transition between a free molecule in isotropic potential and being fixed by a rigid confinement. The NO radical is particularly suited for such an investigation, since the g factor of the free molecule in its ²Π_1∕2 rotational ground state will change between zero (Mendt and Pöppl, 2015) to a g matrix, in which all parameters are close to the free electron value for the rigidly localized radical (Chiesa et al., 2010). In case the axial molecular symmetry is maintained by the environment allowing free rotation about its axis, the g parameter g₃, being assigned to the NO bond axis, is predicted to vanish. The measured value g₃=0.77(5) is indicative of an intermediate situation of the radical and yields information about the locking potential's deviation from axial symmetry. This 17 meV asymmetry as found here is quite small compared to the situation in polycrystalline or amorphous matrices ranging from 300 to 500 meV. The analysis of the spin relaxation times resulted in an activation temperature of about 3 K, assigned to temperature-activated motion of the radical with coupled rotational and translational degrees of freedom in the complicated three-dimensional potential provided by the cage.

Performing ENDOR, the ¹⁴N hyperfine coupling parameters were determined. The experimental values are in fair agreement with predictions from a DFT calculation. The spectral resolution was not sufficient to discriminate between parameter sets expected for the X-ray crystallography-confirmed “up”/“down” configurations of the radical with respect to the orifice of the cage.

The g matrix parameters did not show any temperature dependence in the range of 3.6 to 12 K, in which a dramatic orientation-dependent decrease in $T_{\mathrm{2}}^{\ast }$ is observed. This indicates that the radical is localized, not allowing for excitation of rotational modes about its axis, which would modify the g₃ value. Apparently only low-energy modes with small amplitude around their equilibrium orientation are excited at these temperatures. It should be noted, however, that the accuracy of the data analysis is high enough to detect a small difference in g parameters using cages with slightly modified orifices. It will be interesting to see in the future whether advanced computational methods will be able to reproduce g matrix and hfi tensor data for this radical in such a complicated potential.

Appendix A: Additional figures

Figure A1 Top view of the DFT-optimized structure of NO@C60-OH3 with N “up”. The modified C₆₀ cage is represented by sticks except van der Waals spheres for the oxygen and hydrogen atoms of the orifice and the caged NO – C (grey), H (white), N (blue), O (red), and S (yellow).

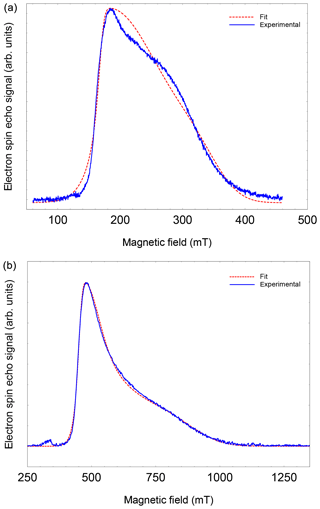
Figure A2 FSE spectra of NO@C60-OH3 (T=5 K) with best fits. (a) S-band (3.5 GHz, 10 mM/CS₂). (b) X-band (9.7 GHz, 2.5 mM/CS₂).

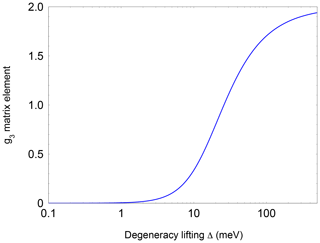
Figure A3 Dependence of the pseudo-axial g₃ matrix element of the NO radical as a function of ${}^{\mathrm{2}}{\mathit{\pi }}_x^{\ast }$ and ${}^{\mathrm{2}}{\mathit{\pi }}_y^{\ast }$ level splitting.

Figure A4 9.7 GHz FSE spectra of NO@C60-OH3 measured at 3.6, 4.1, and 5 K. Using a rather short pulse repetition time (1 ms), the high-field part of the spectrum is partially saturated.

Appendix B: Additional table

Table B1 Best fit parameters for the NO@C60-OH3 spectra measured at different temperatures (data not shown).