the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
SORDOR pulses: expansion of the Böhlen–Bodenhausen scheme for low-power broadband magnetic resonance
Jens D. Haller
David L. Goodwin
A novel type of efficient broadband pulse, called second-order phase dispersion by optimised rotation (SORDOR), has recently been introduced. In contrast to adiabatic excitation, SORDOR-90 pulses provide effective transverse 90∘ rotations throughout their bandwidth, with a quadratic offset dependence of the phase in the x,y plane. Together with phase-matched SORDOR-180 pulses, this enables the Böhlen–Bodenhausen broadband refocusing approach for linearly frequency-swept pulses to be extended to any type of 90∘/180∘ pulse–delay sequence. Example pulse shapes are characterised in theory and experiment, and an example application is given with a 19F-PROJECT experiment for measuring relaxation times with reduced distortions due to J-coupling evolution.
- Article
(2467 KB) - Full-text XML
-
Supplement
(1622 KB) - BibTeX
- EndNote
Many magnetic resonance applications require the manipulation of spins over a large bandwidth under severe restrictions concerning available radiofrequency (rf) amplitude and/or tolerable rf energy. With the advent of 1.2 GHz NMR spectrometers, a large number of experiments require the use of amplitude- and phase-modulated pulses due to the enlarged bandwidths that need to be covered, and equally modern pulsed EPR spectroscopy at any field strength benefits substantially from the use of shaped pulses (Doll and Jeschke, 2014; Spindler et al., 2015, 2017; Jeschke, 2019). However, even conventional NMR spectroscopy at intermediate field strengths at e.g. 600 MHz gain enormously from shaped pulses in conventional carbon-correlated experiments (Ogura et al., 1996; Hwang et al., 1997; Kupc̆e and Freeman, 1997; Cano et al., 2002; Armstrong et al., 2004; Skinner et al., 2006; Tzvetkova et al., 2007; Enthart et al., 2008) and even more so with particular nuclei like 19F, 31P, 15N, 119Sn, and 195Pt (Enders et al., 2014; Power et al., 2016; Lingel et al., 2020).
A multitude of composite and shaped pulses has been designed to cope with the bandwidth problem (Levitt, 1982; Shaka and Freeman, 1983; Warren, 1984; Tycko et al., 1985a; Levitt, 1986; Lurie, 1986; Shaka and Pines, 1987; Freeman et al., 1988; Zax et al., 1988; Ewing et al., 1990; Keniry and Sanctuary, 1992; Hull, 1994; Kobzar et al., 2004, 2008; Ehni and Luy, 2012), with recent pulse shapes optimised using algorithms derived from optimal control theory (Conolly et al., 1986; Mao et al., 1986; Rosenfeld and Zur, 1996; Skinner et al., 2003; Kobzar et al., 2005; Spindler et al., 2012; Ehni and Luy, 2012, 2013, 2014; Koos et al., 2015, 2017) being close to physical limits (Kobzar et al., 2004, 2008, 2012). Whenever only a single component of magnetisation vectors needs to be transferred, excitation and inversion pulses, as members of point-to-point (PP) pulses, provide very efficient solutions (Shaka, 1985; Emsley and Bodenhausen, 1990; Garwood and Ke, 1991; Abramovich and Vega, 1993; Kupc̆e and Freeman, 1994; Barker et al., 2001; Smith et al., 2001; Cano et al., 2002; Skinner et al., 2003, 2004, 2005, 2006; Gershenzon et al., 2007; Coote et al., 2021); regardless, only universal rotation (UR) pulses can be used as full replacements of conventional, bandwidth-limited, hard pulses. UR pulses, however, are especially demanding regarding both rf amplitude and rf energy (Tycko et al., 1985a, b; Cho and Pines, 1987; Shaka and Pines, 1987; Levitt, 1988; Garwood and Ke, 1991; Wimperis, 1991, 1994; Emsley and Bodenhausen, 1992; Poon and Henkelman, 1992, 1995; Abramovich and Vega, 1993; Luy et al., 2005; Brown, 2011; Anand et al., 2012; Kobzar et al., 2012; Moore et al., 2012; Odedra and Wimperis, 2012; Skinner et al., 2012; Altenhof et al., 2019).
To reduce such demands, several concepts involving matching pulse shapes have been developed. Possibly the first such concept based on adiabatic pulses has been reported by Böhlen and Bodenhausen, requiring matched, linear-frequency-swept excitation and inversion pulses (Böhlen et al., 1989, 1990; Burghardt et al., 1990). Depending on the offset ωz, adiabatic excitation transforms z magnetisation into transverse magnetisation with pulse-dependent phase angles α(ωz) with respect to the x axis. A following matched adiabatic inversion pulse provides an effective rotation around the phase α(ωz)+φ with either constant or linearly offset-dependent phase φ. As the effective pulse phases are matched in this concept, the inversion pulses act as refocusing (UR-180) pulses whose effective rotation axes exhibit a quadratic offset dependence due to the adiabatic linear frequency sweep. A more general concept without the restriction on linear frequency sweeps is the COOP concept introduced by Braun and Glaser (Braun and Glaser, 2010, 2014; Asami et al., 2018). However, here too excitation pulse shapes introduced so far are PP pulses, resulting in limited applicability.
Here we propose the recently introduced second-order phase dispersion by optimised rotation (SORDOR) pulses of Goodwin et al. (2020) for an extension of the Böhlen–Bodenhausen concept for a widely applicable cooperative broadband-shaped pulse scenario, in which 90∘ universal rotations are directly realised. SORDOR pulses are not adiabatic and define a new class of low-energy pulse shapes that cause a defined rotation with a constant rotation angle over a specified bandwidth like common UR pulses. Instead of the constant rotation axes of conventional UR pulses, SORDOR pulses show a quadratic offset-dependent phase change of the effective rotation axes in the x,y plane, similar to the linear adiabatic sweeps in the Böhlen–Bodenhausen concept. If a simple quadratic-phase correction of spectra can be applied, SORDOR pulses can be used as a direct replacement of 90 and 180∘ hard pulses. In addition, scaled SORDOR-180 pulses allow full refocusing of magnetisation. The SORDOR pulses therefore represent a direct implementation of the Böhlen–Bodenhausen concept of matched quadratic-phase pulses to the requirements of 90∘-based mixing. After an introduction of pulse properties, their application in NMR spectroscopy is demonstrated experimentally.
SORDOR pulses used here have been optimised as described in the reference (Goodwin et al., 2020): effective propagation for a single spin is given by the n piecewise constant elements of the pulse shape as Ueff=Un…U1, which is subsequently used to calculate a quality factor
where the target propagator is defined by
with
where β defines the desired effective flip angle, α a phase in the x,y plane, ωz the offset, Ix and Iy the usual spin operators represented by the corresponding Pauli matrices, the desired offset range Ω, the pulse length tp, an arbitrary scaling factor , and an arbitrary constant phase α0. Note that the entire shaped pulse is condensed to a single term within the effective propagator and, hence, it directly describes the effective rotation induced by the shaped pulse.
It is evident from the target propagator that a uniform rotation angle β is targeted, resulting in a pulse class termed B1 pulses (not to be mistaken with B1 fields), as defined originally by Levitt (1986) (an extensive description of different pulse classes is given in the Supplement). However, in addition to the minimum requirement of class B1 pulses, an offset-dependent target phase for the effective rotation axes in the x,y plane is applied. Such a phase was originally introduced with ICEBERG pulses of Gershenzon et al. (2008), but, in contrast to the linear ICEBERG phase, the SORDOR target phase varies with a quadratic function of the offset ωz. Other phase-dependent control targets were investigated more recently by Altenhof et al. (2019) and Coote et al. (2021). The quadratic SORDOR phase resembles the quadratic phase being acquired in linear-frequency-swept adiabatic inversion pulses (Baum et al., 1985; Kupc̆e and Freeman, 1995; Garwood and DelaBarre, 2001; Tal and Frydman, 2010; Jeschke et al., 2015), which can be used advantageously, as will be shown below.
Using the GRAPE algorithm (Khaneja et al., 2005; de Fouquieres et al., 2011; de Fouquieres, 2012; Goodwin and Kuprov, 2016) with exact gradients (Van Loan, 1978; Goodwin and Kuprov, 2015) as discussed in detail in Goodwin et al. (2020), pulses for β=90∘ and β=180∘ were obtained, named SORDOR-90 and SORDOR-180, respectively. While the optimisation of SORDOR-180 pulses turned out to be straightforward, good SORDOR-90 pulses were only obtained after introducing a morphing procedure in the optimisation algorithm (morphic-GRAPE), in which the scaling factor Q and the pulse length tp are slowly adjusted from extrema.
The morphic-GRAPE procedure to produce the SORDOR pulses of Goodwin et al. (2020) used four directional morphs to produce high-fidelity 90 and 180∘ pulses. The highest-fidelity pulses for a bandwidth of 40 kHz, unsurprisingly, were at the longest durations, tp=450 µs, with rf amplitudes of 10 kHz. Following on from those optimisations, the SORDOR pulses used in this work introduce an additional directional morph stage: a ramping stage to increase the desired bandwidth to Ω=50 kHz. To this end, the SORDOR pulses ramp 450 µs pulses from 40 to 50 kHz, over (these Q values are used as the high-performance SORDOR pulses lay in this range), in increments of 1 kHz.
Increasing the desired bandwidth lowers the pulse performance Φ. To gain higher performance, the SORDOR pulses ramped to Ω=50 kHz are further expanded to longer pulse durations from 450 to 750 µs, over the best-performing Q from the ramped stage: . The best-performing SORDOR pair, at a nominal pulse duration tp=720 µs, occurred at Q=0.80, and this pulse pair was further optimised for ±5 % B1 inhomogeneity over a Gaussian distribution of rf-amplitude multipliers.
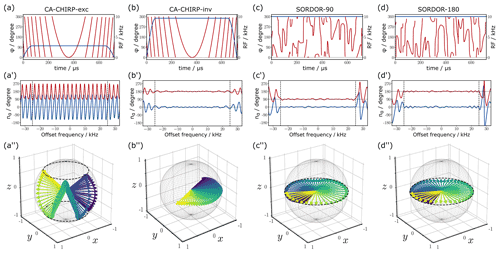
Figure 1Comparison of a constant adiabaticity chirped excitation pulse (CA-Chirp-exc), a chirped inversion pulse (CA-Chirp-inv), a SORDOR-90, and the matched SORDOR-180 pulse. (a–d) Pulse rf amplitudes and phases. (a'–d') Offset dependencies of the (red) and z components (blue) of the effective rotations for the specific pulses. (a”–d”) Visualisations of the normalised rotational axes of the different pulses for a reduced offset region. Colour coding is used to indicate equal offset frequencies for respective pairs of CA-Chirp and SORDOR pulses. Note that the Chirp excitation pulse does not perform a direct universal 90∘ rotation, while SORDOR-90 does.
The resulting SORDOR-90 and SORDOR-180 pulse pair with identical phase dependence α(ωz) is shown in Fig. 1 together with constant-adiabaticity chirped excitation and inversion (Khaneja, 2017; Foroozandeh, 2020) pulses (CA-Chirp-exc and CA-Chirp-inv) for comparison. The SORDOR pulse shapes have a constant rf amplitude of 10 kHz and in both cases a smooth rf phase, even if the course of the rf phase looks somewhat erratic. The CA-Chirp-exc pulse, instead, has a lower rf amplitude of only 2850 Hz and the well-known smooth rf-phase behaviour. The reason for the difference in rf-energy consumption of the SORDOR-90 and CA-Chirp-exc pulse can be seen in the analysis of resulting effective rotations (Fig. 1): while the SORDOR-90 at all offsets essentially resembles pure 90∘ rotations with rotational axes in the x,y plane, the CA-Chirp-exc pulse resembles a classical PP excitation pulse with effective rotations in the range of 90–270∘ and a periodic elevation of the rotational axes along z with the offset. This is the typical behaviour of a class B2 pulse, which is explained in more detail in the Supplement. The SORDOR-180 pulse shows the very same rotation behaviour as the SORDOR-90 pulse, just with an effective 180∘ rotation angle in the x,y plane throughout the optimised offset range. As such it resembles very much the behaviour of the CA-Chirp-inv pulse of the same duration and rf amplitude. However, the SORDOR-180 pulse is directly matched in its phase behaviour to the SORDOR-90 pulse, which for an adiabatic inversion pulse would only accidentally be the case.
A systematic study of SORDOR-90 and SORDOR-180 pulse performances Φ for optimal Q values around 0.75 and a bandwidth of 40 kHz as reported in the reference (Goodwin et al., 2020) is shown in Fig. 2: with increasing pulse lengths the logarithmic quality factor for pulse performance steadily increases in both cases. As in previous studies exploring the physical limits (Kobzar et al., 2004, 2008, 2012), the increase does not describe a smooth function, but as a guide to the eye the pulse performance can be roughly described by a linear function (see Fig. 2). Also, BURBOP-90 and BURBOP-180 pulses, which can be considered special SORDOR pulses with Q=0, follow a similar curve (Kobzar et al., 2012), but for the same performance approximately twice the amount of rf energy is needed for the 180∘ case and about a factor of 1.8 for the 90∘ case. The energy consumption of SORDOR-180 pulses therefore resembles that of time-optimal broadband inversion pulse (BIP) and broadband inversion by optimised pulses (BIBOP) inversion pulses (Smith et al., 2001; Kobzar et al., 2004), while the energy consumption of SORDOR-90 pulses lies in between time-optimal broadband excitation by optimised pulses (BEBOP) excitation and broadband universal rotation by optimised pulses (BURBOP) universal rotation 90∘ pulses.
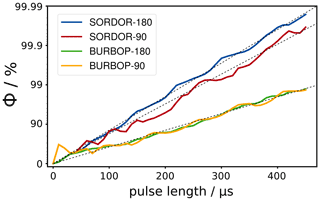
Figure 2Offset-averaged quality factors Φ for different optimised SORDOR and BURBOP pulse shapes with rf amplitudes of 10 kHz and optimised bandwidths of 40 kHz. SORDOR-180 pulses of the same quality consume approximately half the rf energy as corresponding BURBOP-180 UR pulses. SORDOR-90 compared to time-optimal BURBOP-90 pulses lead to a reduction in pulse length and rf energy of approximately a factor of 1.8.
Following the Böhlen and Bodenhausen concept (Böhlen et al., 1989, 1990; Burghardt et al., 1990), which lately has found a revival in EPR spectroscopy (Doll and Jeschke, 2016, 2017a, b), the quadratic-phase SORDOR pulses can directly be used to replace pulses in any hard-pulse–delay sequence. The concept is schematically shown for the perfect echo sequence (Takegoshi et al., 1989) in Fig. 3: a train of 90 and 180∘ pulses with delays ensures planar mixing conditions and therefore spin state conservation and in-phase to in-phase transfer. The sequence works well with hard pulses, but offset limitations sometimes require the application of broadband pulses. As the SORDOR pulses have matched quadratic-phase effective rotation axes at each optimised frequency offset, they directly act as universal rotation pulses, thereby enabling excitation as well as refocusing and mixing. Assuming that a SORDOR pulse sequence initially acts on polarisation, it will represent a broadband version of the hard-pulse sequence. The only difference to the hard-pulse version affects the acquisition, as the quadratic phase implies the use of a quadratic-phase correction (see below) or the application of a scaled SORDOR-180 pulse for phase refocusing. Simulations show that a matched SORDOR-180 pulse with rf amplitude and pulse length scaled by and , respectively, leads to effective refocusing of transverse magnetisation for acquisition without phase correction (see also the experimental section and Fig. 4e).
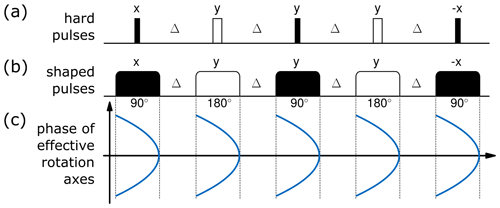
Figure 3Schematic of the applicability of the Böhlen and Bodenhausen concept. (a) Hard-pulse perfect echo sequence; (b) corresponding shaped pulse scheme; (c) phase of effective rotation axes of SORDOR pulses with quadratic-phase dependence.
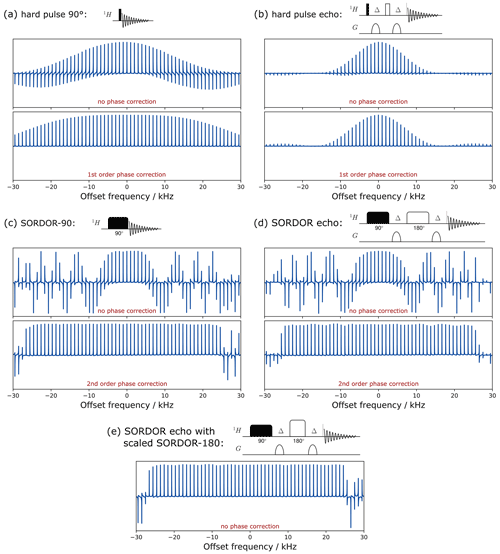
Figure 4Experimental excitation profiles of a hard 90∘ (a) and SORDOR-90 (c) pulse as well as a 90∘–Δ–180∘–Δ echo element for hard and SORDOR pulses (b, d) and a combination of SORDOR pulses with a scaled SORDOR-180 pulse (e). Offset profiles of pulses are shown without phase correction and with linear (first-order, a and b) and quadratic (second-order, c and d) phase correction. The echo element with the SORDOR-180 scaled by as described in the main text is self-refocusing and results in a perfect phase over the optimised bandwidth without phase correction (e). The Bruker AU program used for second-order phase correction is given in the Supplement.
The offset-dependent experimental performance of a single SORDOR-90 pulse and a combination SORDOR-90–Δ–SORDOR-180–Δ acquisition is shown in Fig. 4 in comparison to corresponding hard-pulse elements. Applied gradients furthermore ensure that the desired coherence pathway is selected. While a single rectangular 90∘ pulse results in a perfectly phaseable spectrum over large bandwidths, the 90∘–Δ–180∘–Δ sequence has a clearly reduced bandwidth. Also, the signal intensities are rapidly reduced with the offset for the two hard-pulse scenarios. The SORDOR-90 pulse, instead, produces a horribly looking offset dependence, which, however, results in nearly constant amplitude signals over the optimised bandwidth if a quadratic-phase correction is applied. Deviations of signal intensity over the optimised bandwidth are generally below ±2 %. Equally, the SORDOR pulse combination results in nicely refocused spectra after the second-order phase correction with deviations generally below ±4 %. A particularly interesting case for applications is shown in Fig. 4e, where the echo element is applied with a SORDOR-180 pulse with rf amplitude increased and pulse length decreased by . In this case the transverse magnetisation is fully refocused, resulting in purely absorptive signals without any phase correction.
The applicability of the SORDOR pulse pair is demonstrated in a second example using 1H- and 19F-PROJECT experiments for the measurement of relaxation times without distortions due to coupling evolution (Takegoshi et al., 1989; Aguilar et al., 2012). We applied the SORDOR-PROJECT sequence with two different SORDOR pairs and a hard-pulse PROJECT sequence to a doped D2O sample for comparing the effective relaxation rates of the residual HDO singlet. With decay times of 0.179 s (hard pulse), 0.178 s (±10 % B1-corrected SORDOR pair), and 0.169 s (±10 % B1-corrected SORDOR-pair), the relaxation measurements appear to give reproducible results, although the SORDOR-PROJECT experiment resulted in slightly stronger deviations from exponential decay (see the Supplement for data).
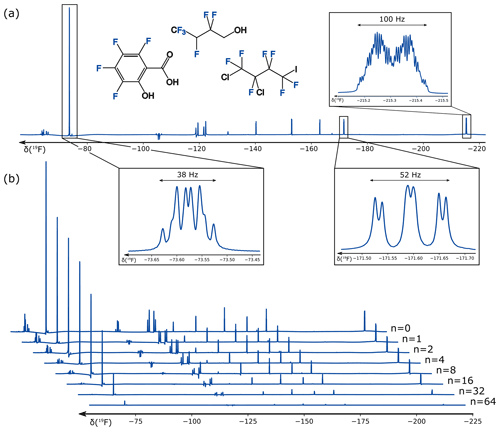
Figure 519F-PROJECT experiment (Aguilar et al., 2012) for relaxation measurement based on multiple SORDOR perfect echoes (n=0–64) with Δ=3 ms and SORDOR pulse lengths tp of 576 µs each (b). In addition, zooms for several large multiplets for the PROJECT spectrum with n=4 are given (a) with annotated multiplet widths.
For the 19F-PROJECT experiment, corresponding spectra are shown in Fig. 5 for a mixture of 1,1,1,2,3,3-hexafluoro-4-butanol, 1,2-dichloro-4-iodo-heptafluoro-n-butane and 1,2,3,4-tetrafluoro-salicylic acid in DMSO with 19F chemical shifts ranging from −63 to −216 ppm. On the Avance III HD 400 MHz spectrometer used, this corresponds to a bandwidth of 58 kHz, which can be easily covered by the SORDOR pulse pair with rf amplitudes of 12.5 kHz. Clearly the relaxation of all signals can be easily followed using up to 64 perfect echoes with delays of Δ=3 ms and corresponding 576 µs SORDOR-90 and SORDOR-180 pulses, which add with 432 µs (75 %) per pulse to the effective delay. Thereby it is important to note that phase distortions due to coupling evolution are expected for a sum of couplings significantly larger than . We therefore had a closer look at the multiplets with large couplings that frequently appear in fluorinated compounds. Remarkably, most multiplets with widths up to 100 Hz still result in pure absorptive PROJECT spectra, demonstrating the robustness of the refocusing properties of the SORDOR approach. Only signals with apparent second-order artefacts at −63 to −68, −104 to −109, and −118 to −123 ppm show larger distortions. The spectra of all well-refocused signals result in mono-exponential decays from which decay times are easily derived. Spectra with apparent second-order artefacts are expected to show distorted decays (see the Supplement for decay plots and data). It should be noted that we also acquired hard-pulse 19F-PROJECT experiments to validate data. However, resulting spectra – even when applied on-resonant – were heavily distorted and did not allow any extraction of decays. This is due to the insufficient bandwidth of accessible hard pulses, which leads to absorptive and dispersive contributions of in-phase as well as anti-phase magnetisation in the heavily coupled fluorine spin systems.
Matched SORDOR-90 and SORDOR-180 pulses form a novel class of pulses with uniform rotation angles and a specific quadratic offset dependence of corresponding rotation axes. With such pulses the refocusing concepts of Böhlen and Bodenhausen for quadratic-phase pulses can generally be implemented. The SORDOR implementation allows the direct replacement of 90 and 180∘ hard pulses in pulse–delay sequences.
As the simplest application, the concept allows the acquisition of 1D-type spectra with only an additional quadratic-phase correction. The AU program for Bruker spectrometers used for Fig. 4 to perform a quadratic-phase correction is given in the Supplement. This quadratic-phase correction is always the same for a given pulse and can be determined once and then applied in all types of experiment with excitation using the same SORDOR-90 pulse.
In more complex pulse–delay experiments, like the PROJECT sequence shown in Fig. 5 for a 19F application, hard 90∘ and 180∘ pulses can directly be replaced by SORDOR-90 and SORDOR-180 pulses. If the last part of the sequence before acquisition consists of a Δ–180∘–Δ element, the quadratic-phase correction of the acquired FID may be compensated by using the scaled SORDOR-180 approach demonstrated in Fig. 4e. In this case the transverse magnetisation is fully refocused by applying scaling factors of and to rf amplitude and pulse length tp, respectively.
In 2D experiments, the indirect dimension can be evolved as in conventional hard-pulse experiments the offset dependencies for excitation and back transfer along z compensate each other.
A disadvantage of the SORDOR pulses arises in hetero-nuclear experiments when pulses on different nuclei need to be applied simultaneously. In these cases the same precautions apply that must also be taken, i.e. for adiabatic or other shaped pulses (Khaneja, 2018; Foroozandeh, 2020). Simultaneously applied hard pulses should be aligned to either the left- or right-hand side of the SORDOR pulses. Central application of pulses would need to be considered for a specific SORDOR pulse in use, e.g. with a toggling frame approach as demonstrated for selective pulses in INEPT-transfer elements (Haller et al., 2019; Ehni et al., 2021). Simultaneous application with other shaped pulses may also lead to unexpected effects, as coupling evolution might take place during the pulses (Ehni et al., 2021). Even if hard pulses are aligned left or right from the SORDOR pulses, offset-dependent coupling evolution cannot be avoided. However, in this case it is well-defined, and in the 1H,13C correlation experiment it can be used like in Chirp applications to compensate for offset-dependent coupling-size compensation (Kupc̆e and Freeman, 1997; Zwahlen et al., 1997).
In homo-nuclear experiments artefacts may arise from homo-nuclear coupling evolution during pulse shapes. Average Hamiltonian simulations on the non-adiabatic SORDOR pulse shapes used here, however, reveal that this effect is negligibly small, in contrast to adiabatic pulses with known considerable coupling effects (data not shown). Essentially only unavoidable artefacts for spin systems with close chemical shifts and second-order contributions must be taken into account.
It should be noted that the proposed approach considers that resonance frequencies during delays stay the same. Exchange effects and radiation damping will lead to offset changes and because of the offset-dependent rotation axes finally to distorted phases. Such distortions may be undesired or even helpful in the identification of e.g. exchange processes.
Finally, we would like to make the remark that the relatively short SORDOR pulses used in this study are compensated for ±5 % B1 inhomogeneity with overall quality factors Φ>0.9999. This quality factor corresponds to a quite good performance, as can be seen in Fig. 4. For probe heads exceeding the assumed ±5 % B1 inhomogeneity, pulse performance might be reduced. We also experienced slightly reduced performance with high Q probe heads and correspondingly long switching times. To improve experimental performance, pulse shape optimisation eventually requires the adaptation of optimisation procedures with penalty functions regarding non-smooth waveforms (Goodwin and Kuprov, 2016; Goodwin, 2017) or non-adiabaticity (Rosenfeld and Zur, 1996; Brif et al., 2014), which will be subject to future efforts.
An implementation of the Böhlen and Bodenhausen concept using matched SORDOR-90 and SORDOR-180 pulse pairs is introduced. While SORDOR-180 pulses are equivalent to broadband inversion pulses with a defined, matched phase behaviour, corresponding SORDOR-90 pulses as introduced in Goodwin et al. (2020) belong to the B1 pulse class and allow uniform 90∘ rotations around specific, quadratic offset-dependent rotation axes. The concept allows the direct replacement of hard pulses by their SORDOR equivalents, including 90∘ mixing pulses, thereby enabling very broadband planar mixing and COSY-type experiments. As such, SORDOR pulse pairs act equivalently to universal rotation pulses but with considerably shorter pulse lengths and reduced rf energy. As an example, we introduced a broadband 19F-PROJECT experiment with good refocusing and mixing results even for complex multiplets.
SORDOR-180 pulses afford the same rf energy as time-optimal inversion pulses like BIP (Smith et al., 2001) or BIBOP (Kobzar et al., 2004) pulses of the same quality. SORDOR-90 pulses require slightly more rf energy than time-optimal BEBOP excitation pulses (Kobzar et al., 2004) but significantly less than corresponding BURBOP-90 time-optimal UR pulses (Kobzar et al., 2012). Therefore the SORDOR pulse pair represents the direct implementation of a broadband 90∘/180∘ pulse–delay sequence with very low rf-energy deposition, with a reduction factor of rf requirements compared to conventional UR pulses slightly below 2. With this improvement in rf usage, we expect the introduced approach to be useful in a variety of experiments like fast-pulsing 2Ds (see e.g. Kupc̆e and Freeman, 2007; Schulze-Sünninghausen et al., 2014, 2017) and rf-limited imaging applications (Barker et al., 2001; Frankel et al., 2018).
Pulses are available at https://www.ioc.kit.edu/luy/111.php (Haller et al., 2022), and codes can be found in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/mr-3-53-2022-supplement.
JDH contributed to pulse development, theory, experiments, analysis, and writing of the manuscript. DLG contributed to pulse development, theory, analysis, and writing of the manuscript. BL contributed to pulse development, theory, experiments, analysis, and writing of the manuscript.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
David L. Goodwin thanks Martin Koos and Stella Slad for useful discussions on the 19F-NMR and the PROJECT sequence. Burkhard Luy is grateful to Marcel Utz (Southampton) for intense discussions that finally led to the SORDOR project. He also thanks the HGF programme Information (43.35.02) and the Deutsche Forschungsgemeinschaft for financial support (LU 835/13-1).
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. LU 835/13-1) and the Helmholtz-Gemeinschaft (Information, grant no. 43.35.02).
The article processing charges for this open-access publication were covered by the Karlsruhe Institute of Technology (KIT).
This paper was edited by Patrick Giraudeau and reviewed by two anonymous referees.
Abramovich, D. and Vega, S.: Derivation of Broadband and Narrowband Excitation Pulses Using the Floquet Formalism, J. Magn. Reson. A, 105, 30–48, https://doi.org/10.1006/jmra.1993.1245, 1993. a, b
Aguilar, J. A., Nilsson, M., Bodenhausen, G., and Morris, G. A.: Spin echo NMR spectra without J modulation, Chem. Commun., 48, 811–813, https://doi.org/10.1039/c1cc16699a, 2012. a, b
Altenhof, A. R., Lindquist, A. W., Foster, L. D. D., Holmes, S. T., and Schurko, R. W.: On the use of frequency-swept pulses and pulses designed with optimal control theory for the acquisition of ultra-wideline NMR spectra, J. Magn. Reson., 309, 106612, https://doi.org/10.1016/j.jmr.2019.106612, 2019. a, b
Anand, C. K., Bain, A. D., Curtis, A. T., and Nie, Z.: Designing optimal universal pulses using second-order, large-scale, non-linear optimization, J. Magn. Reson., 219, 61–74, https://doi.org/10.1016/j.jmr.2012.04.004, 2012. a
Armstrong, G. S., Cano, K. E., Mandelshtam, V. A., Shaka, A. J., and Bendiak, B.: Rapid 3D NMR using the filter diagonalization method: application to oligosaccharides derivatized with 13C-labeled acetyl groups, J. Magn. Reson., 170, 156–63, https://doi.org/10.1016/j.jmr.2004.06.002, 2004. a
Asami, S., Kallies, W., Gunther, J. C., Stavropoulou, M., Glaser, S. J., and Sattler, M.: Ultrashort Broadband Cooperative Pulses for Multidimensional Biomolecular NMR Experiments, Angew. Chem. Int. Ed., 57, 14498–14502, https://doi.org/10.1002/anie.201800220, 2018. a
Barker, P. B., Golay, X., Artemov, D., Ouwerkerk, R., Smith, M. A., and Shaka, A. J.: Broadband proton decoupling for in vivo brain spectroscopy in humans, Magn. Reson. Med., 45, 226–232, https://doi.org/10.1002/1522-2594(200102)45:2<226::AID-MRM1031>3.0.CO;2-Z, 2001. a, b
Baum, J., Tycko, R., and Pines, A.: Broadband and adiabatic inversion of a two-level system by phase-modulated pulses, Phys. Rev. A, 32, 3435–3447, https://doi.org/10.1103/physreva.32.3435, 1985. a
Böhlen, J.-M., Rey, M., and Bodenhausen, G.: Refocusing with chirped pulses for broadband excitation without phase dispersion, J. Magn. Reson., 84, 191–197, https://doi.org/10.1016/0022-2364(89)90018-8, 1989. a, b
Böhlen, J.-M., Burghardt, I., Rey, M., and Bodenhausen, G.: Frequency-modulated “Chirp” pulses for broadband inversion recovery in magnetic resonance, J. Magn. Reson., 90, 183–191, https://doi.org/10.1016/0022-2364(90)90377-l, 1990. a, b
Braun, M. and Glaser, S. J.: Cooperative pulses, J. Magn. Reson., 207, 114–123, https://doi.org/10.1016/j.jmr.2010.08.013, 2010. a
Braun, M. and Glaser, S. J.: Concurrently optimized cooperative pulses in robust quantum control: application to broadband Ramsey-type pulse sequence elements, New J. Phys., 16, 115002, https://doi.org/10.1088/1367-2630/16/11/115002, 2014. a
Brif, C., Grace, M. D., Sarovar, M., and Young, K. C.: Exploring adiabatic quantum trajectories via optimal control, New J. Phys., 16, 065013, https://doi.org/10.1088/1367-2630/16/6/065013, 2014. a
Brown, D.: Constant amplitude broadband refocusing pulses from numerical optimization, Magn. Reson. Chem., 49, 705–709, https://doi.org/10.1002/mrc.2806, 2011. a
Burghardt, I., Böhlen, J., and Bodenhausen, G.: Broadband multiple‐quantum nuclear magnetic resonance with frequency‐modulated “chirp” pulses: Applications to pairs of scalar‐coupled spin nuclei, J. Chem. Phys., 93, 7687–7697, https://doi.org/10.1063/1.459348, 1990. a, b
Cano, K. E., Smith, M. A., and Shaka, A. J.: Adjustable, broadband, selective excitation with uniform phase, J. Magn. Reson., 155, 131–139, https://doi.org/10.1006/jmre.2002.2506, 2002. a, b
Cho, H. and Pines, A.: Iterative maps for broadband excitation of transverse coherence in two level systems, J. Chem. Phys., 86, 6591–6601, https://doi.org/10.1063/1.452405, 1987. a
Conolly, S., Nishimura, D., and Macovski, A.: Optimal control solutions to the magnetic resonance selective excitation problem, IEEE Trans. Med. Imaging, 5, 106–15, https://doi.org/10.1109/TMI.1986.4307754, 1986. a
Coote, P., Bermel, W., and Arthanari, H.: Optimization of phase dispersion enables broadband excitation without homonuclear coupling artifacts, J. Magn. Reson., 325, 106928, https://doi.org/10.1016/j.jmr.2021.106928, 2021. a, b
de Fouquieres, P.: Implementing quantum gates by optimal control with doubly exponential convergence, Phys. Rev. Lett., 108, 110504, https://doi.org/10.1103/PhysRevLett.108.110504, 2012. a
de Fouquieres, P., Schirmer, S. G., Glaser, S. J., and Kuprov, I.: Second order gradient ascent pulse engineering, J. Magn. Reson., 212, 412–7, https://doi.org/10.1016/j.jmr.2011.07.023, 2011. a
Doll, A. and Jeschke, G.: Fourier-transform electron spin resonance with bandwidth-compensated chirp pulses, J. Magn. Reson., 246, 18–26, https://doi.org/10.1016/j.jmr.2014.06.016, 2014. a
Doll, A. and Jeschke, G.: EPR-correlated dipolar spectroscopy by Q-band chirp SIFTER, Phys. Chem. Chem. Phys., 18, 23111–23120, https://doi.org/10.1039/c6cp03067j, 2016. a
Doll, A. and Jeschke, G.: Double electron-electron resonance with multiple non-selective chirp refocusing, Phys. Chem. Chem. Phys., 19, 1039–1053, https://doi.org/10.1039/c6cp07262c, 2017a. a
Doll, A. and Jeschke, G.: Wideband frequency-swept excitation in pulsed EPR spectroscopy, J. Magn. Reson., 280, 46–62, https://doi.org/10.1016/j.jmr.2017.01.004, 2017b. a
Ehni, S. and Luy, B.: A systematic approach for optimizing the robustness of pulse sequence elements with respect to couplings, offsets, and B1-field inhomogeneities (COB), Magn. Reson. Chem., 50, S63–S72, https://doi.org/10.1002/mrc.3846, 2012. a, b
Ehni, S. and Luy, B.: BEBEtr and BUBI: J-compensated concurrent shaped pulses for 1H-13C experiments, J. Magn. Reson., 232, 7–17, https://doi.org/10.1016/j.jmr.2013.04.007, 2013. a
Ehni, S. and Luy, B.: Robust INEPT and refocused INEPT transfer with compensation of a wide range of couplings, offsets, and B1-field inhomogeneities (COB3), J. Magn. Reson., 247, 111–117, https://doi.org/10.1016/j.jmr.2014.07.010, 2014. a
Ehni, S., Koos, M. R. M., Reinsperger, T., Haller, J. D., Goodwin, D. L., and Luy, B.: Concurrent J-Evolving Refocusing Pulses, arXiv [preprint], arXiv:2109.05453, 12 September 2021. a, b
Emsley, L. and Bodenhausen, G.: Gaussian pulse cascades: New analytical functions for rectangular selective inversion and in-phase excitation in NMR, Chem. Phys. Lett., 165, 469–476, https://doi.org/10.1016/0009-2614(90)87025-m, 1990. a
Emsley, L. and Bodenhausen, G.: Optimization of shaped selective pulses for NMR using a quaternion description of their overall propagators, J. Magn. Reson., 97, 135–148, https://doi.org/10.1016/0022-2364(92)90242-y, 1992. a
Enders, M., Görling, B., Braun, A. B., Seltenreich, J. E., Reichenbach, L. F., Rissanen, K., Nieger, M., Luy, B., Schepers, U., and Bräse, S.: Cytotoxicity and NMR Studies of Platinum Complexes with Cyclooctadiene Ligands, Organometallics, 33, 4027–4034, https://doi.org/10.1021/om500540x, 2014. a
Enthart, A., Freudenberger, J. C., Furrer, J., Kessler, H., and Luy, B.: The CLIP/CLAP-HSQC: pure absorptive spectra for the measurement of one-bond couplings, J. Magn. Reson., 192, 314–22, https://doi.org/10.1016/j.jmr.2008.03.009, 2008. a
Ewing, B., Glaser, S. J., and Drobny, G. P.: Development and optimization of shaped NMR pulses for the study of coupled spin systems, Chem. Phys., 147, 121–129, https://doi.org/10.1016/0301-0104(90)85028-u, 1990. a
Foroozandeh, M.: Spin dynamics during chirped pulses: applications to homonuclear decoupling and broadband excitation, J. Magn. Reson., 318, 106768, https://doi.org/10.1016/j.jmr.2020.106768, 2020. a, b
Frankel, J., Wilén, J., and Hansson Mild, K.: Assessing Exposures to Magnetic Resonance Imaging's Complex Mixture of Magnetic Fields for In Vivo, In Vitro, and Epidemiologic Studies of Health Effects for Staff and Patients, Front. Public Health, 6, 66, https://doi.org/10.3389/fpubh.2018.00066, 2018. a
Freeman, R., Friedrich, J., and Wu, X. L.: A Pulse for All Seasons – Fourier-Transform Spectra without a Phase Gradient, J. Magn. Reson., 79, 561–567, https://doi.org/10.1016/0022-2364(88)90092-3, 1988. a
Garwood, M. and DelaBarre, L.: The return of the frequency sweep: designing adiabatic pulses for contemporary NMR, J. Magn. Reson., 153, 155–177, https://doi.org/10.1006/jmre.2001.2340, 2001. a
Garwood, M. and Ke, Y.: Symmetric pulses to induce arbitrary flip angles with compensation for rf inhomogeneity and resonance offsets, J. Magn. Reson., 94, 511–525, https://doi.org/10.1016/0022-2364(91)90137-i, 1991. a, b
Gershenzon, N. I., Kobzar, K., Luy, B., Glaser, S. J., and Skinner, T. E.: Optimal control design of excitation pulses that accommodate relaxation, J. Magn. Reson., 188, 330–336, https://doi.org/10.1016/j.jmr.2007.08.007, 2007. a
Gershenzon, N. I., Skinner, T. E., Brutscher, B., Khaneja, N., Nimbalkar, M., Luy, B., and Glaser, S. J.: Linear phase slope in pulse design: application to coherence transfer, J. Magn. Reson., 192, 235–243, https://doi.org/10.1016/j.jmr.2008.02.021, 2008. a
Goodwin, D. L.: Advanced Optimal Control Methods for Spin Systems, PhD thesis, University of Southampton, https://doi.org/10.5258/soton/t0003, 2017. a
Goodwin, D. L. and Kuprov, I.: Auxiliary matrix formalism for interaction representation transformations, optimal control, and spin relaxation theories, J. Chem. Phys., 143, 084113, https://doi.org/10.1063/1.4928978, 2015. a
Goodwin, D. L. and Kuprov, I.: Modified Newton-Raphson GRAPE methods for optimal control of spin systems, J. Chem. Phys., 144, 204107, https://doi.org/10.1063/1.4949534, 2016. a, b
Goodwin, D. L., Koos, M. R. M., and Luy, B.: Second order phase dispersion by optimized rotation pulses, Phys. Rev. Research, 2, 033157, https://doi.org/10.1103/PhysRevResearch.2.033157, 2020. a, b, c, d, e, f
Haller, J. D., Bodor, A., and Luy, B.: Real-time pure shift measurements for uniformly isotope-labeled molecules using X-selective BIRD homonuclear decoupling, J. Magn. Reson., 302, 64–71, https://doi.org/10.1016/j.jmr.2019.03.011, 2019. a
Haller, J. D., Goodwin, D. L., and Luy, B.: Pulse Shapes, Karlsruher Institut für Technologie (KIT) [data set], https://www.ioc.kit.edu/luy/111.php, last access: 25 April 2022. a
Hull, W. E.: Experimental aspects of two-dimensional NMR, in: Two-dimensional NMR Spectroscopy – Applications for Chemists and Biochemists, edited by: Croasmun, W. R. and Carlson, R. M. K., VCH Publishers, New York, 67–456, https://doi.org/10.1016/S0003-2670(00)84174-4, 1994. a
Hwang, T. L., van Zijl, P. C., and Garwood, M.: Broadband adiabatic refocusing without phase distortion, J. Magn. Reson., 124, 250–4, https://doi.org/10.1006/jmre.1996.1049, 1997. a
Jeschke, G.: Quo vadis EPR?, J. Magn. Reson., 306, 36–41, https://doi.org/10.1016/j.jmr.2019.07.008, 2019. a
Jeschke, G., Pribitzer, S., and Doll, A.: Coherence Transfer by Passage Pulses in Electron Paramagnetic Resonance Spectroscopy, J. Phys. Chem. B, 119, 13570–13582, https://doi.org/10.1021/acs.jpcb.5b02964, 2015. a
Keniry, M. A. and Sanctuary, B. C.: Experimental-Verification of Composite Inversion Pulses Obtained by Series Expansion of the Offset Angle, J. Magn. Reson., 97, 382–384, https://doi.org/10.1016/0022-2364(92)90322-X, 1992. a
Khaneja, N.: Chirp excitation, J. Magn. Reson., 282, 32–36, https://doi.org/10.1016/j.jmr.2017.07.003, 2017. a
Khaneja, N.: Chirp mixing, Chem. Phys. Lett., 704, 62–67, https://doi.org/10.1016/j.cplett.2018.05.047, 2018. a
Khaneja, N., Reiss, T., Kehlet, C., Schulte-Herbrüggen, T., and Glaser, S. J.: Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms, J. Magn. Reson., 172, 296–305, https://doi.org/10.1016/j.jmr.2004.11.004, 2005. a
Kobzar, K., Skinner, T. E., Khaneja, N., Glaser, S. J., and Luy, B.: Exploring the limits of broadband excitation and inversion pulses, J. Magn. Reson., 170, 236–243, https://doi.org/10.1016/j.jmr.2004.06.017, 2004. a, b, c, d, e, f
Kobzar, K., Luy, B., Khaneja, N., and Glaser, S. J.: Pattern pulses: design of arbitrary excitation profiles as a function of pulse amplitude and offset, J. Magn. Reson., 173, 229–235, https://doi.org/10.1016/j.jmr.2004.12.005, 2005. a
Kobzar, K., Skinner, T. E., Khaneja, N., Glaser, S. J., and Luy, B.: Exploring the limits of broadband excitation and inversion: II. Rf-power optimized pulses, J. Magn. Reson., 194, 58–66, https://doi.org/10.1016/j.jmr.2008.05.023, 2008. a, b, c
Kobzar, K., Ehni, S., Skinner, T. E., Glaser, S. J., and Luy, B.: Exploring the limits of broadband 90 degrees and 180 degrees universal rotation pulses, J. Magn. Reson., 225, 142–160, https://doi.org/10.1016/j.jmr.2012.09.013, 2012. a, b, c, d, e
Koos, M. R. M., Feyrer, H., and Luy, B.: Broadband excitation pulses with variable RF amplitude-dependent flip angle (RADFA), Magn. Reson. Chem., 53, 886–893, https://doi.org/10.1002/mrc.4297, 2015. a
Koos, M. R. M., Feyrer, H., and Luy, B.: Broadband RF-amplitude-dependent flip angle pulses with linear phase slope, Magn. Reson. Chem., 55, 797–803, https://doi.org/10.1002/mrc.4593, 2017. a
Kupc̆e, Ē. and Freeman, R.: Wideband Excitation with Polychromatic Pulses, J. Magn. Reson. A, 108, 268–273, https://doi.org/10.1006/jmra.1994.1123, 1994. a
Kupc̆e, Ē. and Freeman, R.: Adiabatic Pulses for Wideband Inversion and Broadband Decoupling, J. Magn. Reson. A, 115, 273–276, https://doi.org/10.1006/jmra.1995.1179, 1995. a
Kupc̆e, Ē. and Freeman, R.: Compensation for Spin–Spin Coupling Effects during Adiabatic Pulses, J. Magn. Reson., 127, 36–48, https://doi.org/10.1006/jmre.1997.1193, 1997. a, b
Kupc̆e, Ē. and Freeman, R.: Fast multidimensional NMR by polarization sharing, Magn. Reson. Chem., 45, 2–4, https://doi.org/10.1002/mrc.1931, 2007. a
Levitt, M. H.: Symmetrical composite pulse sequences for NMR population inversion. I. Compensation of radiofrequency field inhomogeneity, J. Magn. Reson., 48, 234–264, https://doi.org/10.1016/0022-2364(82)90275-x, 1982. a
Levitt, M. H.: Composite pulses, Progr. Nucl. Magn. Reson. Spectrosc., 18, 61–122, https://doi.org/10.1016/0079-6565(86)80005-x, 1986. a, b
Levitt, M. H.: NMR Solvent Peak Suppression by Nonlinear Excitation, J. Chem. Phys., 88, 3481–3496, https://doi.org/10.1063/1.453897, 1988. a
Lingel, A., Vulpetti, A., Reinsperger, T., Proudfoot, A., Denay, R., Frommlet, A., Henry, C., Hommel, U., Gossert, A. D., Luy, B., and Frank, A. O.: Comprehensive and High-Throughput Exploration of Chemical Space Using Broadband 19F NMR-Based Screening, Angew. Chem. Int. Ed., 59, 14809–14817, https://doi.org/10.1002/anie.202002463, 2020. a
Lurie, D. J.: Numerical design of composite radiofrequency pulses, J. Magn. Reson., 70, 11–20, https://doi.org/10.1016/0022-2364(86)90359-8, 1986. a
Luy, B., Kobzar, K., Skinner, T. E., Khaneja, N., and Glaser, S. J.: Construction of universal rotations from point-to-point transformations, J. Magn. Reson., 176, 179–86, https://doi.org/10.1016/j.jmr.2005.06.002, 2005. a
Mao, J., Mareci, T. H., Scott, K. N., and Andrew, E. R.: Selective inversion radiofrequency pulses by optimal control, J. Magn. Reson., 70, 310–318, https://doi.org/10.1016/0022-2364(86)90016-8, 1986. a
Moore, J., Jankiewicz, M., Anderson, A. W., and Gore, J. C.: Evaluation of non-selective refocusing pulses for 7 T MRI, J. Magn. Reson., 214, 212–220, https://doi.org/10.1016/j.jmr.2011.11.010, 2012. a
Odedra, S. and Wimperis, S.: Use of composite refocusing pulses to form spin echoes, J. Magn. Reson., 214, 68–75, https://doi.org/10.1016/j.jmr.2011.10.006, 2012. a
Ogura, K., Terasawa, H., and Inagaki, F.: Fully 13C-Refocused Multidimensional 13C-Edited Pulse Schemes Using Broadband Shaped Inversion and Refocusing Pulses, J. Magn. Reson. B, 112, 63–68, https://doi.org/10.1006/jmrb.1996.0110, 1996. a
Poon, C. S. and Henkelman, R. M.: 180∘ refocusing pulses which are insensitive to static and radiofrequency field inhomogeneity, J. Magn. Reson., 99, 45–55, https://doi.org/10.1016/0022-2364(92)90154-y, 1992. a
Poon, C. S. and Henkelman, R. M.: Robust Refocusing Pulses of Limited Power, J. Magn. Reson. A, 116, 161–180, https://doi.org/10.1006/jmra.1995.0005, 1995. a
Power, J. E., Foroozandeh, M., Adams, R. W., Nilsson, M., Coombes, S. R., Phillips, A. R., and Morris, G. A.: Increasing the quantitative bandwidth of NMR measurements, Chem. Commun., 52, 2916–2919, https://doi.org/10.1039/c5cc10206e, 2016. a
Rosenfeld, D. and Zur, Y.: Design of adiabatic selective pulses using optimal control theory, Magn. Reson. Med., 36, 401–409, https://doi.org/10.1002/mrm.1910360311, 1996. a, b
Schulze-Sünninghausen, D., Becker, J., and Luy, B.: Rapid heteronuclear single quantum correlation NMR spectra at natural abundance, J. Am. Chem. Soc., 136, 1242–1245, https://doi.org/10.1021/ja411588d, 2014. a
Schulze-Sünninghausen, D., Becker, J., Koos, M. R. M., and Luy, B.: Improvements, extensions, and practical aspects of rapid ASAP-HSQC and ALSOFAST-HSQC pulse sequences for studying small molecules at natural abundance, J. Magn. Reson., 281, 151–161, https://doi.org/10.1016/j.jmr.2017.05.012, 2017. a
Shaka, A. J.: Composite pulses for ultra-broadband spin inversion, Chem. Phys. Lett., 120, 201–205, https://doi.org/10.1016/0009-2614(85)87040-8, 1985. a
Shaka, A. J. and Freeman, R.: Composite pulses with dual compensation, J. Magn. Reson., 55, 487–493, https://doi.org/10.1016/0022-2364(83)90133-6, 1983. a
Shaka, A. J. and Pines, A.: Symmetric phase-alternating composite pulses, J. Magn. Reson., 71, 495–503, https://doi.org/10.1016/0022-2364(87)90249-6, 1987. a, b
Skinner, T. E., Reiss, T. O., Luy, B., Khaneja, N., and Glaser, S. J.: Application of optimal control theory to the design of broadband excitation pulses for high-resolution NMR, J. Magn. Reson., 163, 8–15, https://doi.org/10.1016/s1090-7807(03)00153-8, 2003. a, b
Skinner, T. E., Reiss, T. O., Luy, B., Khaneja, N., and Glaser, S. J.: Reducing the duration of broadband excitation pulses using optimal control with limited RF amplitude, J. Magn. Reson., 167, 68–74, https://doi.org/10.1016/j.jmr.2003.12.001, 2004. a
Skinner, T. E., Reiss, T. O., Luy, B., Khaneja, N., and Glaser, S. J.: Tailoring the optimal control cost function to a desired output: application to minimizing phase errors in short broadband excitation pulses, J. Magn. Reson., 172, 17–23, https://doi.org/10.1016/j.jmr.2004.09.011, 2005. a
Skinner, T. E., Kobzar, K., Luy, B., Bendall, M. R., Bermel, W., Khaneja, N., and Glaser, S. J.: Optimal control design of constant amplitude phase-modulated pulses: application to calibration-free broadband excitation, J. Magn. Reson., 179, 241–249, https://doi.org/10.1016/j.jmr.2005.12.010, 2006. a, b
Skinner, T. E., Gershenzon, N. I., Nimbalkar, M., Bermel, W., Luy, B., and Glaser, S. J.: New strategies for designing robust universal rotation pulses: application to broadband refocusing at low power, J. Magn. Reson., 216, 78–87, https://doi.org/10.1016/j.jmr.2012.01.005, 2012. a
Smith, M. A., Hu, H., and Shaka, A. J.: Improved broadband inversion performance for NMR in liquids, J. Magn. Reson., 151, 269–283, https://doi.org/10.1006/jmre.2001.2364, 2001. a, b, c
Spindler, P. E., Zhang, Y., Endeward, B., Gershernzon, N., Skinner, T. E., Glaser, S. J., and Prisner, T. F.: Shaped optimal control pulses for increased excitation bandwidth in EPR, J. Magn. Reson., 218, 49–58, https://doi.org/10.1016/j.jmr.2012.02.013, 2012. a
Spindler, P. E., Waclawska, I., Endeward, B., Plackmeyer, J., Ziegler, C., and Prisner, T. F.: Carr-Purcell Pulsed Electron Double Resonance with Shaped Inversion Pulses, J. Phys. Chem. Lett., 6, 4331–4335, https://doi.org/10.1021/acs.jpclett.5b01933, 2015. a
Spindler, P. E., Schöps, P., Kallies, W., Glaser, S. J., and Prisner, T. F.: Perspectives of shaped pulses for EPR spectroscopy, J. Magn. Reson., 280, 30–45, https://doi.org/10.1016/j.jmr.2017.02.023, 2017. a
Takegoshi, K., Ogura, K., and Hikichi, K.: A perfect spin echo in a weakly homonuclear J-coupled two spin-12 system, J. Magn. Reson., 84, 611–615, https://doi.org/10.1016/0022-2364(89)90127-3, 1989. a, b
Tal, A. and Frydman, L.: Single-scan multidimensional magnetic resonance, Prog. Nucl. Magn. Reson. Spectrosc., 57, 241–292, https://doi.org/10.1016/j.pnmrs.2010.04.001, 2010. a
Tycko, R., Cho, H. M., Schneider, E., and Pines, A.: Composite pulses without phase distortion, J. Magn. Reson., 61, 90–101, https://doi.org/10.1016/0022-2364(85)90270-7, 1985a. a, b
Tycko, R., Pines, A., and Guckenheimer, J.: Fixed point theory of iterative excitation schemes in NMR, J. Chem. Phys., 83, 2775–2802, https://doi.org/10.1063/1.449228, 1985b. a
Tzvetkova, P., Simova, S., and Luy, B.: P.E.HSQC: a simple experiment for simultaneous and sign-sensitive measurement of (1JCH+DCH) and (2JHH+DHH) couplings, J. Magn. Reson., 186, 193–200, https://doi.org/10.1016/j.jmr.2007.02.009, 2007. a
Van Loan, C.: Computing integrals involving the matrix exponential, IEEE Trans. Automat. Contr., 23, 395–404, https://doi.org/10.1109/tac.1978.1101743, 1978. a
Warren, W. S.: Effects of arbitrary laser or NMR pulse shapes on population inversion and coherence, J. Chem. Phys., 81, 5437–5448, https://doi.org/10.1063/1.447644, 1984. a
Wimperis, S.: Iterative schemes for phase-distortionless composite 180∘ pulses, J. Magn. Reson., 93, 199–206, https://doi.org/10.1016/0022-2364(91)90043-s, 1991. a
Wimperis, S.: Broadband, Narrowband, and Passband Composite Pulses for Use in Advanced NMR Experiments, J. Magn. Reson. A, 109, 221–231, https://doi.org/10.1006/jmra.1994.1159, 1994. a
Zax, D. B., Goelman, G., and Vega, S.: Amplitude-Modulated Composite Pulses, J. Magn. Reson., 80, 375–382, https://doi.org/10.1016/0022-2364(88)90312-5, 1988. a
Zwahlen, C., Legault, P., Vincent, S. J. F., Greenblatt, J., Konrat, R., and Kay, L. E.: Methods for Measurement of Intermolecular NOEs by Multinuclear NMR Spectroscopy: Application to a Bacteriophage λ N-Peptide/boxB RNA Complex, J. Am. Chem. Soc., 119, 6711–6721, https://doi.org/10.1021/ja970224q, 1997. a





