Geminal parahydrogen-induced polarization: accumulating long-lived singlet order on methylene proton pairs

In the majority of hydrogenative parahydrogen-induced polarization (PHIP) experiments, the hydrogen molecule undergoes pairwise cis addition to an unsaturated precursor to occupy vicinal positions on the product molecule. However, some ruthenium-based hydrogenation catalysts induce geminal hydrogenation, leading to a reaction product in which the two hydrogen atoms are transferred to the same carbon centre, forming a methylene (CH₂) group. The singlet order of parahydrogen is substantially retained over the geminal hydrogenation reaction, giving rise to a singlet-hyperpolarized CH₂ group. Although the T₁ relaxation times of the methylene protons are often short, the singlet order has a long lifetime, provided that singlet–triplet mixing is suppressed, either by chemical equivalence of the protons or by applying a resonant radiofrequency field. The long lifetime of the singlet order enables the accumulation of hyperpolarization during the slow hydrogenation reaction. We introduce a kinetic model for the behaviour of the observed hyperpolarized signals, including both the chemical kinetics and the spin dynamics of the reacting molecules. Our work demonstrates the feasibility of producing singlet-hyperpolarized methylene moieties by parahydrogen-induced polarization. This potentially extends the range of molecular agents which may be generated in a hyperpolarized state by chemical reactions of parahydrogen.

1 Introduction

Nuclear magnetic resonance (NMR) suffers from intrinsically low sensitivity, in part because of the small interaction energies between nuclear spins and magnetic fields. Hyperpolarization techniques alleviate this problem by generating nuclear spin systems with a high degree of nuclear spin polarization, enhancing the nuclear magnetization by many orders of magnitude (Ardenkjaer-Larsen et al., 2003; Maly et al., 2008; Bowers and Weitekamp, 1987; Walker and Happer, 1997; Kovtunov et al., 2018). Parahydrogen-induced polarization (PHIP) (Bowers and Weitekamp, 1987; Natterer and Bargon, 1997; Adams et al., 2009) is a hyperpolarization method which utilizes hydrogen (H₂) gas enriched in the para-spin isomer; the enrichment is carried out by cooling H₂ gas over a suitable catalyst. There are two main modes of PHIP: (i) in hydrogenative PHIP, the strongly enhanced nuclear singlet order of para-enriched H₂ gas is substantially conserved through a pairwise catalytic transfer of the hydrogen pair onto a product molecule (Bowers and Weitekamp, 1987; Natterer and Bargon, 1997; Reineri et al., 2015). The high degree of nuclear singlet order in the hydrogenation product is converted into enhanced nuclear magnetization by symmetry-breaking nuclear spin interactions; (ii) in the signal amplification by reversible exchange (SABRE) method, reversible chemical processes are used to transfer the nuclear singlet order onto the target molecules (Adams et al., 2009; Theis et al., 2014; Truong et al., 2015; Lindale et al., 2019; Zhang et al., 2019). PHIP has several advantages over alternative hyperpolarization techniques, such as its low cost, its compact and simple equipment requirements, and its ability to produce relatively large amounts of hyperpolarized material in a short time.

This article concerns hydrogenative PHIP experiments, which involve in most cases the vicinal positioning of the hydrogen substituents; i.e. the hydrogen atoms become attached to adjacent carbon atoms in the product molecule. Furthermore, in the case that a carbon–carbon triple bond is hydrogenated, the hydrogenation product usually has the cis geometry; i.e. the two hydrogen atoms end up on the same side of the resulting double bond. This reaction specificity strongly limits the range of hyperpolarized substances accessible to hydrogenative PHIP.

Recent advances in catalytic chemistry have uncovered alternative modes of hydrogenation (Harthun et al., 1996; Leutzsch et al., 2015; Guthertz et al., 2018; Fürstner, 2019). For example, some ruthenium-based catalysts achieve trans-vicinal hydrogenation, meaning that the two hydrogen atoms are transferred to opposite sides of the resulting double bond (Leutzsch et al., 2015). This phenomenon allows the hyperpolarization of the important metabolite fumarate in aqueous solution (Ripka et al., 2018; Eills et al., 2019). Furthermore, under some circumstances, geminal hydrogenation is observed, meaning that the two hydrogen atoms become bonded to the same carbon in the product molecule (Guthertz et al., 2018; Song et al., 2019). If para-enriched H₂ is used, the result is a methylene (CH₂) moiety in which the proton pair exhibits strongly enhanced nuclear singlet order, meaning a population difference between the nuclear singlet and triplet states (Carravetta et al., 2004; Carravetta and Levitt, 2004; Levitt, 2012, 2019; Zhang et al., 2019). If the product molecule has sufficiently low symmetry, the CH₂ protons are magnetically inequivalent, allowing symmetry-breaking spin interactions to convert the nuclear singlet order into hyperpolarized nuclear magnetization. Since methylene groups are ubiquitous in metabolites and natural products, gem-PHIP could potentially open up a new range of PHIP-based hyperpolarization targets.

One difficulty with gem-PHIP is that the associated hydrogenation reaction is usually slow (Song et al., 2019). Furthermore, the short internuclear distance between the CH₂ protons leads to a strong dipole–dipole interaction, which provides an efficient T₁ mechanism and hence rapid decay of hyperpolarized magnetization. The combination of a slow production rate of spin order with a short relaxation time T₁ leads to weak hyperpolarization, with poor enhancement factors and low polarization levels.

Although the T₁ values of methylene protons are usually short, their singlet relaxation times T_S can be long, exceeding 2 min in some cases (Carravetta and Levitt, 2004). In most cases, these long singlet lifetimes are not immediately manifest, since symmetry-breaking interactions such as chemical shift differences between the CH₂ protons mix the long-lived singlet state with the rapidly relaxing triplet states. Experimental intervention is usually needed to suppress singlet–triplet mixing, either by transferring the sample to a low magnetic field (Carravetta et al., 2004; Carravetta and Levitt, 2005; Pileio et al., 2010; Kiryutin et al., 2019) or by applying a resonant radiofrequency (rf) field (Carravetta and Levitt, 2004; Gopalakrishnan and Bodenhausen, 2006; Pileio and Levitt, 2009).

In this article we investigate the accumulation of a long-lived hyperpolarized singlet order on methylene protons during a gem-PHIP experiment by application of a spin-locking rf field during the slow chemical reaction (Hübler et al., 2000). We introduce a kinetic model to describe the observed hyperpolarization levels during experiments and provide a theoretical analysis of the spin dynamics.

2 Geminal hydrogenation

The geminal hydrogenation reaction studied in this paper is shown in Fig. 1. It involves the hydrogenation of acetylenedicarboxylate (top left), catalysed by the ruthenium complex [Cp^∗Ru(CH₃CN)₃]PF₆ in D₂O solution. The main product of this reaction is the trans-vicinal hydrogenation product, fumarate (Ripka et al., 2018) (see Appendix B). However, in some conditions, the side product I is also formed (the systematic name for I and an NMR spectrum of the reaction mixture are given in the Supplement). The side reaction is inhibited by sodium sulfite (Ripka et al., 2018). In the current work, sodium sulfite was not used, favouring generation of the geminal hydrogenation product I. The postulated reaction mechanism involves formation of a carbene intermediate (Guthertz et al., 2018) between the catalyst and first acetylenedicarboxylate molecule, followed by a [3+2] cycloaddition with a second acetylenedicarboxylate molecule, dissociation of the ruthenium adduct, and abstraction of a deuterium atom from the D₂O solvent.

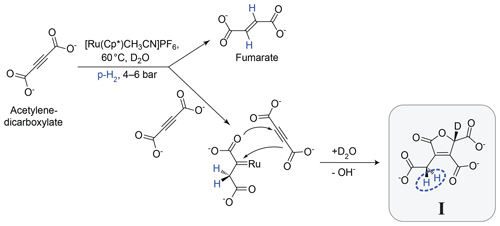
Figure 1 Postulated mechanism for the formation of I. The main hydrogenation reaction leads to the product fumarate. A side reaction, involving a second acetylenedicarboxylate molecule, leads to the product I. The inequivalent methylene (CH₂) protons which derive from para-enriched hydrogen are shown in blue.

I is prone to decomposition and further reactions and could not be isolated and subjected to standard characterization methods. As described in the Supplement, the structure of I was verified by synthesizing a compound with the same structure by an alternative route, followed by a comparison of the ¹H NMR spectra.

This paper focuses on the two CH₂ protons of the product molecule I which derive from the para-enriched H₂ reagent. This proton pair is highlighted in blue in Fig. 1. The chemical equivalence of these CH₂ protons is broken by the chiral centre four bonds away, on the opposite side of the five-membered ring.

Figure 2 shows the CH₂ region of the ¹H NMR spectrum of the reaction product. The black spectrum is the Fourier transform of the NMR signal induced by a single π∕2 pulse, obtained 90 s after the conclusion of the chemical reaction with para-enriched hydrogen. It displays a typical AB pattern, albeit with some spectral intensity distortions from residual hyperpolarization effects (see Appendix B for further explanation). The two protons have a chemical shift difference of Δδ=0.197 ppm and a two-bond J coupling of ${|}^{\mathrm{2}}J|=\mathrm{16.8}$ Hz.

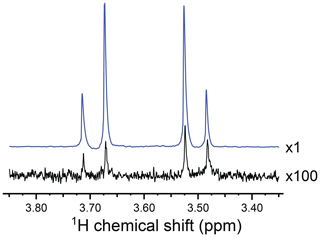
Figure 2 Partial ¹H NMR spectra of the reaction products at a resonance frequency of 400.0 MHz and temperature of 333 K, showing the signals from the CH₂ group of I. The hyperpolarized spectrum (blue) was acquired in a gem-PHIP experiment using the pulse sequence in Fig. 3a, with the intervals τ₁=90 s and τ₂=90 s. The spectrum in black was obtained by waiting 90 s after the conclusion of the experiment and taking the Fourier transform of the NMR signal induced by a single π∕2 pulse. The spectrum shows an AB peak pattern, with intensity distortions from residual hyperpolarization. The AB spectrum is consistent with a chemical shift difference of Δδ=0.197 ppm and a two-bond J coupling of ${|}^{\mathrm{2}}J|=\mathrm{16.8}$ Hz. The signal enhancement factor in the gem-PHIP experiment is estimated to be ∼300, which corresponds to a ¹H polarization level of ∼0.9 %.

The nuclear spin relaxation characteristics of I were estimated at room temperature (295 K) and a magnetic field of 9.4 T, using standard techniques (see Supplement). The spin-lattice relaxation time of the CH₂ protons is given by $T_{\mathrm{1}}=\mathrm{1.23}\pm \mathrm{0.14}$ s. The singlet relaxation time of the CH₂ protons under the same conditions is $T_{\text{S}}=\mathrm{61.1}\pm \mathrm{7.1}$ s. Unfortunately, the chemical instability of I made it difficult to estimate the relaxation times under the much warmer conditions of the gem-PHIP reaction (333 K; see Sect. 5). As described in the Supplement, molecule I decomposes by losing one carboxylic acid group to give an achiral reaction product. The decomposition occurs on a timescale of roughly 2 h at 333 K.

3 Results

3.1 gem-PHIP

Parahydrogen-induced hyperpolarization of I was demonstrated using the pulse sequence in Fig. 3a. Bubbling of para-enriched hydrogen was conducted for an interval τ₁=90 s in the presence of a radiofrequency spin-locking field (Hübler et al., 2000), whose frequency corresponds to the mean chemical shift of the CH₂ protons. The spin-locking field amplitude corresponded to a ¹H nutation frequency of ${\mathit{\omega }}_{\mathrm{nut}}/\mathrm{2}\mathit{\pi }=\mathrm{1.0}$ kHz. Bubbling was switched off and the spin locking continued for a further interval of τ₂=30 s. This gave time for the bubbles to dissipate and for a hyperpolarized singlet order to accumulate during the ongoing hydrogenation reaction.

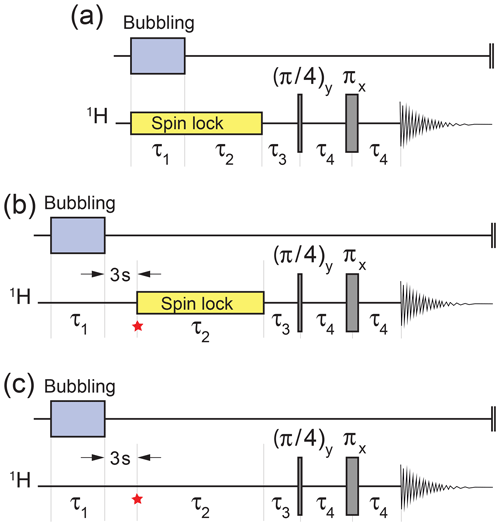
Figure 3 Experimental timing sequences. (a) Procedure for the demonstration of gem-PHIP. Bubbling of para-enriched H₂ is conducted for an interval τ₁ in the presence of a radio-frequency spin-locking field in order to suppress singlet–triplet mixing in the reaction product I. The spin locking continues for a further interval τ₂, followed by a two-pulse sequence to convert the hyperpolarized singlet order to in-phase magnetization (Sarkar et al., 2007). The experimental delays were τ₃=6.49 ms and τ₄=14.97 ms. (b) Procedure for demonstrating the accumulation of the singlet order during spin locking. The spin-lock field is applied during the variable interval τ₂, with an amplitude corresponding to a nutation frequency ${\mathit{\omega }}_{\mathrm{nut}}/\left(\mathrm{2}\mathit{\pi }\right)=\mathrm{1.0}$ kHz. The star symbol refers to the time point discussed in the text. (c) The same sequence as for panel (b) but without spin locking during the variable τ₂ interval. The interval τ₁ was set to 90 s for panel (a) and 17 s for panels (b) and (c).

Hyperpolarized singlet order was converted into in-phase magnetization by the sequence of three delays and two radiofrequency pulses shown in Fig. 3. This sequence converts magnetization into singlet order in weakly coupled spin-1∕2 pairs (Sarkar et al., 2007). The ideal values of the pulse sequence delays, in the case of infinitely short pulses, are ${\mathit{\tau }}_{\mathrm{3}}=|\mathit{\pi }/{\mathit{\omega }}_{\mathrm{\Delta }}|$ and ${\mathit{\tau }}_{\mathrm{4}}=\mathrm{1}/\left(\mathrm{4}J\right)$, where the chemical shift frequency difference is ω_Δ=ω⁰Δδ and ω⁰ is the Larmor frequency. In practice, the following pulse sequence intervals were used: τ₃=6.49 ms and τ₄=14.97 ms.

Figure 2 shows the ¹H NMR spectrum of I, hyperpolarized by gem-PHIP (blue spectrum). The NMR signals of the CH₂ protons are enhanced by a factor of ∼300 as compared to the spectrum taken 90 s after the end of the pulse sequence (black spectrum). This enhancement factor corresponds to a modest polarization level of ∼0.9 %. Although the achieved polarization level is not spectacular, this experiment demonstrates the feasibility of the gem-PHIP of methylene protons, provided that a spin-locking field is used to stabilize the hyperpolarized singlet order.

3.2 Hyperpolarization decay

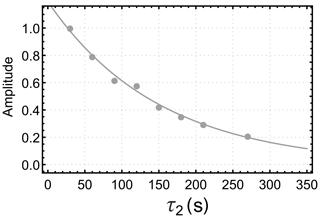
Figure 4 shows the dependence of the integrated gem-PHIP signal intensity on the spin-locking interval τ₂ in Fig. 3a, with the bubbling time τ₁ increased to 90 s. Each point in Fig. 4 is the result of an independent experiment, performed on a fresh aliquot of the stock solution, with the signal amplitude normalized against the integrated amplitude of the thermal equilibrium spectrum, obtained 90 s after the pulse sequence has finished. The integrated signal amplitude follows a monoexponential decay function with a time constant of 151±9 s. As discussed below, this time constant may be assigned to the decay time constant T_S for a singlet order in the presence of the spin-locking field.

Figure 4 Dependence of the integrated gem-PHIP signal amplitude for the CH₂ protons of I on the interval τ₂ in the pulse sequence of Fig. 3a, with τ₁ fixed to 90 s. Solid line: fit to Eq. (19) with f_aA_a=1.79, f_aB_a=0 and time constant $T_{\mathrm{S}}^{\mathbf{\text{I}}}=\mathrm{151}$ s for singlet-order decay.

3.3 Accumulation of a hyperpolarized singlet order

The pulse sequence in Fig. 3b was used to study the accumulation of a hyperpolarized singlet order on the CH₂ protons of I during the slow geminal hydrogenation reaction. The experiment started by bubbling para-enriched H₂ gas through the NMR tube for τ₁=17 s, in order to saturate the solution. The sample was then allowed to rest for a settling time of 3 s in order to dissipate bubbles and to achieve good sample and field homogeneity. The trajectory of the hyperpolarized spin order during the subsequent interval was followed by varying the interval τ₂ in a series of independent experiments, each one performed on a separate aliquot of the same stock solution. Experiments were also performed without spin locking during the τ₂ interval (Fig. 3c).

The results of this investigation are shown in Fig. 5. When a spin-locking field is applied during the τ₂ interval (Fig. 3b), the hyperpolarized signals first increase and then decay (orange symbols). If no spin-locking field is applied during the τ₂ interval (Fig. 3c), the hyperpolarized NMR signals decay monotonically with respect to τ₂ (blue symbols).

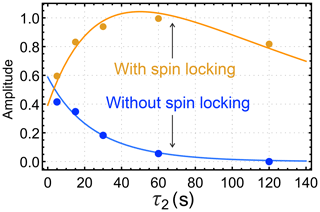
Figure 5 Dependence of the integrated gem-PHIP signal amplitudes of the CH₂ protons of I on the interval τ₂ in the pulse sequences of Fig. 3b and c, with τ₁ fixed to 17 s. The orange symbols show the amplitudes for the case of a spin-locking field during the τ₂ interval (sequence in Fig. 3b), with an amplitude corresponding to the nutation frequency ${\mathit{\omega }}_{\mathrm{nut}}/\mathrm{2}\mathit{\pi }=\mathrm{1.0}$ kHz. The blue symbols show the amplitudes for experiments without a spin-locking field during the τ₂ interval (sequence in Fig. 3c). The orange and blue solid lines show the functions a_b(τ₂) and a_c(τ₂) (Eqs. 19 and 23, respectively), with the parameters $T_{\mathrm{S}}^{\mathbf{\text{I}}}=\mathrm{151}$ s, $T_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}=\mathrm{28.7}$ s, $T_{zz}^{\mathbf{\text{I}}}=\mathrm{13.2}$ s, $f_b{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}\left(\mathrm{0}\right)\times k=\mathrm{0.059}{\mathrm{s}}^{-\mathrm{1}}$, $f_c{C}_{zz}^{\mathbf{\text{I}}}\left(\mathrm{0}\right)=-\mathrm{1.2}$, and f_b=f_c.

4 Kinetic analysis

Figure 6 shows the simplified kinetic model which is used to interpret these results. The dynamics of the system may be analysed in terms of the chemical kinetics of the hydrogenation reaction as well as the spin dynamics of the product molecule I. Although the chemical kinetics depend only on concentrations and physical conditions, the spin-dynamical pathways may be manipulated experimentally with fine time resolution, for example by turning spin-locking fields on and off. The experimental results derive from an interplay between the chemical and spin-dynamical domains. Similar analyses have been performed in different contexts (Kaptein, 1972; Hübler et al., 1999; Goez, 2009; Pravdivtsev et al., 2015; Emondts et al., 2017; Kovtunov et al., 2018; Lindale et al., 2019; Barskiy et al., 2019).

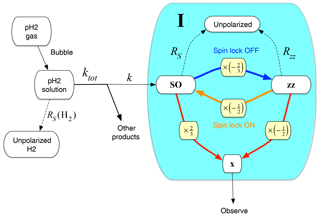
Figure 6 Kinetic model for gem-PHIP. The chemical reaction of para-enriched H₂ with the acetylenedicarboxylate precursor and ruthenium-based catalyst (not shown) proceeds with rate constant k. The shaded area includes the product molecule I in different spin polarization states: unpolarized (top), in a state of singlet nuclear spin order (left), in a state of zz order (right), and with observable x magnetization (bottom). Singlet order decays with rate constant $R_{\mathrm{S}}=T_{\text{S}}^{-\mathrm{1}}$; zz order decays with rate constant $R_{zz}=T_{zz}^{-\mathrm{1}}$. If no spin-locking field is present, singlet order is rapidly converted into zz order, with a conversion factor of $-\mathrm{2}/\mathrm{3}$ (blue arrow and yellow box). If a spin-locking field is applied, zz order is instantaneously projected onto singlet order, with a conversion factor of $-\mathrm{1}/\mathrm{2}$ (orange arrow and yellow box). Singlet order and zz order may be converted into observable x magnetization by the two-pulse sequence in Fig. 3 (red arrows and yellow boxes). The conversion factors in this case are 2∕3 for singlet order and $-\mathrm{1}/\mathrm{2}$ for zz order.

4.1 Chemical kinetics

After para-enriched H₂ gas is introduced into the solution by bubbling, it starts to react with the acetylenedicarboxylate precursor, catalysed by the ruthenium complex. As depicted in Fig. 1, this is a complex process with the generation of several products and with the production of I requiring an additional precursor molecule. Nevertheless, for the sake of simplicity, and since the acetylenedicarboxylate precursor is in excess, the reaction leading to I is assumed to be first order with respect to the para-H₂ reagent and to proceed with rate constant k.

After the bubbling has stopped, the concentrations of the H₂ reagent and the product molecule I are assumed to follow the simple kinetic equations:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\left[{\mathrm{H}}_{\mathrm{2}}\right]}_t=-k_{\mathrm{tot}}{\left[{\mathrm{H}}_{\mathrm{2}}\right]}_t,\\ & {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\left[\mathbf{\text{I}}\right]}_t=+k{\left[{\mathrm{H}}_{\mathrm{2}}\right]}_t,\end{array}\end{array}$$

where k_tot is the rate constant for all hydrogenation reactions, including those that do not lead to the product molecule I, k_tot>k. The differential Eq. (1) is easily solved to show that the solution concentration of H₂ decays exponentially with time, while the concentration of the product molecule I increases:

$$\begin{array}{}\text{(2)}& {\displaystyle }{\left[{\mathrm{H}}_{\mathrm{2}}\right]}_t={\left[{\mathrm{H}}_{\mathrm{2}}\right]}_{\mathrm{0}}\exp (-k_{\mathrm{tot}}t),\text{(3)}& {\displaystyle }{\left[\mathbf{\text{I}}\right]}_t={\left[\mathbf{\text{I}}\right]}_{\mathrm{\infty }}\left(\mathrm{1}-\exp (-kt)\right),\end{array}$$

where the limiting value of the concentration of I is given by

$$\begin{array}{}\text{(4)}& {\left[\mathbf{\text{I}}\right]}_{\mathrm{\infty }}={\displaystyle \frac{k}{k_{\mathrm{tot}}}}{\left[{\mathrm{H}}_{\mathrm{2}}\right]}_{\mathrm{0}}.\end{array}$$

As expected, the limiting yield of I depends on the ratio of the productive rate constant k to the total rate constant of all hydrogenation reactions k_tot.

4.2 Spin dynamics

In this section we discuss some general spin-dynamical scenarios relevant to parahydrogen-enhanced NMR experiments, and in Sect. 4.3 we evaluate the spin dynamics and chemical kinetics specific to the experiments performed in this work. The spin dynamics in this section were evaluated with the assistance of SpinDynamica software (Bengs and Levitt, 2018).

4.2.1 Singlet order

The proton spins of para-enriched H₂ are in a state of enhanced nuclear singlet order, described as the difference between the population of the nuclear singlet state and the mean population of the nuclear triplet states:

$$\begin{array}{}\text{(5)}& \mathbf{SO}=\langle S_{\mathrm{0}}\mathrm{|}\mathit{\rho }\mathrm{|}{S}_{\mathrm{0}}\rangle -{\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\sum _{M=-\mathrm{1}}^{+\mathrm{1}}\langle T_M\mathrm{|}\mathit{\rho }\mathrm{|}{T}_M\rangle ,\end{array}$$

where ρ is the spin density operator, and the singlet and triplet states are defined in terms of the Zeeman product states as follows (Levitt, 2012):

$$\begin{array}{}\text{(6)}& \begin{array}{rl}& \mathrm{|}{S}_{\mathrm{0}}\rangle ={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}\left(\mathrm{|}\mathit{\alpha }\mathit{\beta }\rangle -\mathrm{|}\mathit{\beta }\mathit{\alpha }\rangle \right),\\ & \mathrm{|}{T}_{+\mathrm{1}}\rangle =\mathrm{|}\mathit{\alpha }\mathit{\alpha }\rangle ,\\ & \mathrm{|}{T}_{\mathrm{0}}\rangle ={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}\left(\mathrm{|}\mathit{\alpha }\mathit{\beta }\rangle +\mathrm{|}\mathit{\beta }\mathit{\alpha }\rangle \right),\\ & \mathrm{|}{T}_{-\mathrm{1}}\rangle =\mathrm{|}\mathit{\beta }\mathit{\beta }\rangle .\end{array}\end{array}$$

Singlet order SO may be regarded as the expectation value of the singlet order operator Q_SO, which is defined as follows:

$$\begin{array}{}\text{(7)}& Q_{\mathrm{SO}}=\mathrm{|}{S}_{\mathrm{0}}\rangle \langle S_{\mathrm{0}}\mathrm{|}-{\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\sum _{M=-\mathrm{1}}^{+\mathrm{1}}\mathrm{|}{T}_M\rangle \langle T_M\mathrm{|}=-{\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}{\mathbf{I}}_{\mathrm{1}}\cdot {\mathbf{I}}_{\mathrm{2}},\end{array}$$

so that

$$\begin{array}{}\text{(8)}& \mathbf{SO}=\langle Q_{\mathrm{SO}}\rangle =\mathrm{Tr}\left\{Q_{\mathrm{SO}}^{\mathit{†}}\mathit{\rho }\right\}.\end{array}$$

H₂ gas in thermal equilibrium at room temperature, with an ortho : para ratio very close to 3 : 1, has a negligible singlet order, SO≃0. Pure para-H₂ gas has singlet order SO=1. The current work employs H₂ gas which is enriched with the para-spin isomer by thermal equilibration at 77 K. This yields an ortho : para ratio of approximately 1 : 1, corresponding to a singlet order of $\mathbf{SO}\simeq \mathrm{1}/\mathrm{3}$. Assuming that the nuclear spin states are substantially unchanged through the chemical reaction, the product molecule I is formed with its methylene protons in a similar state of finite singlet order, $\mathbf{SO}\simeq \mathrm{1}/\mathrm{3}$.

The singlet-order operator Q_SO is an exact eigenoperator of the spin propagation superoperator in the case of a magnetically equivalent spin-pair system such as for H₂ gas. However, in the product molecule I, the chiral centre breaks the equivalence of the methylene protons, so that the operator Q_SO is no longer an eigenoperator of the evolution. The chemical shift difference induces singlet–triplet transitions which mix the operator Q_SO with other operators. However, if a sufficiently strong spin-locking field is applied, the singlet–triplet transitions are suppressed, so that the order SO is substantially unchanged during the evolution, except for a decay due to relaxation processes (Pileio and Levitt, 2009). The decay rate constant is given by $R_{\text{S}}=T_{\text{S}}^{-\mathrm{1}}$, where T_S is the time constant for singlet-order decay, which is often much longer than the relaxation time constant T₁ for longitudinal magnetization. The decay of singlet order in the presence of a spin-locking field, with rate constant R_S, is shown in Fig. 6 by the dashed arrow running upwards, connecting the SO state of the reaction product I to the unpolarized state.

4.2.2 zz order

A different type of nuclear spin order is called zz order (Sørensen et al., 1984) and corresponds to the expectation value of an operator Q_zz defined as follows:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& Q_{zz}=\mathrm{2}{I}_{\mathrm{1}z}{I}_{\mathrm{2}z},\\ & \mathbf{zz}=\langle Q_{zz}\rangle =\mathrm{Tr}\left\{Q_{zz}^{\mathit{†}}\mathit{\rho }\right\}.\end{array}\end{array}$$

In the absence of a spin-locking field, and if there is a relatively large chemical shift difference between the coupled spins, the operator Q_zz is a better approximation to an eigenoperator of the spin evolution propagator than the singlet-order operator Q_SO. The relaxation of the system can be complex and multi-exponential in this case. Nevertheless, for the sake of simplicity, we assume here a single rate constant $R_{zz}=T_{zz}^{-\mathrm{1}}$ for the zz order in the absence of a spin-locking field. The time constant T_zz is expected to be close to the ordinary spin-lattice relaxation time constant T₁. The decay of zz order in the absence of a spin-locking field, with rate constant R_zz, is shown in Fig. 6 by the dashed arrow running upwards connecting the zz state of the reaction product I to the unpolarized state.

4.2.3 Spin locking OFF

Suppose that the molecules of I are in a state of enhanced singlet order SO. This state is stable if a spin-locking field is continuously applied and decays monotonically with the time constant T_S. However, if the spin-locking field is turned off, the chemical shift difference between the methylene protons leads to rapid singlet–triplet mixing. The zz-order operator Q_zz is an approximate eigenoperator of the evolution in this case, instead of the singlet-order operator Q_SO. Hence, any singlet order SO which is present when the spin-locking field is turned off is projected onto the zz-order operator Q_zz. The remaining spin order corresponds to zero-quantum coherences which rapidly oscillate and decay. These additional components may be ignored to a good approximation, provided that the spin-locking field remains turned off for an interval that is long compared to the difference in chemical shift frequencies.

The zz order created by this projection process is given by

$$\begin{array}{}\text{(10)}& \mathbf{zz}={\displaystyle \frac{\mathrm{Tr}\left\{Q_{zz}^{\mathit{†}}{Q}_{\mathrm{SO}}\right\}}{\mathrm{Tr}\left\{Q_{zz}^{\mathit{†}}{Q}_{zz}\right\}}}\mathbf{SO}=-{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}\mathbf{SO}.\end{array}$$

The projection of SO onto zz is depicted by the blue arrow in Fig. 6, annotated by the projection factor $-\mathrm{2}/\mathrm{3}$ (yellow box).

4.2.4 Spin locking ON

Suppose that the molecules of I are in a state of enhanced zz order zz. The corresponding operator Q_zz is an eigenoperator of the spin evolution in the absence of a spin-locking field. However, if the spin-locking field is turned on, singlet–triplet mixing is suppressed, and the zz-order operator Q_zz is no longer an eigenoperator of the spin evolution. Any zz order which is present when the spin-locking field is turned on is projected onto the singlet-order operator Q_SO. The remaining spin order corresponds to high-rank spin order terms which rapidly dephase under radiofrequency field inhomogeneity.

The singlet order created by this projection process is given by

$$\begin{array}{}\text{(11)}& \mathbf{SO}={\displaystyle \frac{\mathrm{Tr}\left\{Q_{\mathrm{SO}}^{\mathit{†}}{Q}_{zz}\right\}}{\mathrm{Tr}\left\{Q_{\mathrm{SO}}^{\mathit{†}}{Q}_{\mathrm{SO}}\right\}}}\mathbf{zz}=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathbf{zz}.\end{array}$$

The projection of zz onto SO is depicted by the orange arrow in Fig. 6, annotated by the projection factor $-\mathrm{1}/\mathrm{2}$ (yellow box).

4.2.5 Signal read-out

The spin orders zz and SO are observed by applying the two-pulse sequence given in Fig. 3c and described in Sarkar et al. (2007). This sequence converts both types of spin order into observable transverse magnetization, which induces a time-domain NMR signal in the subsequent interval of free precession. The read-out transformations may be written as follows:

$$\begin{array}{}\text{(12)}& \begin{array}{rl}& U{Q}_{\mathrm{SO}}{U}^{\mathit{†}}=a(\mathbf{SO}\to \mathbf{x})I_x+\mathrm{\dots },\\ & U{Q}_{zz}{U}^{\mathit{†}}=a(\mathbf{zz}\to \mathbf{x})I_x+\mathrm{\dots },\end{array}\end{array}$$

where U is the propagator for the two-pulse sequence and the dots denote operators which are orthogonal to I_x. These amplitudes may be calculated as follows:

$$\begin{array}{}\text{(13)}& \begin{array}{rl}& a(\mathbf{SO}\to \mathbf{x})={\displaystyle \frac{\mathrm{Tr}\left\{I_x^{\mathit{†}}U{Q}_{\mathrm{SO}}{U}^{\mathit{†}}\right\}}{\mathrm{Tr}\left\{I_x^{\mathrm{2}}\right\}}},\\ & a(\mathbf{zz}\to \mathbf{x})={\displaystyle \frac{\mathrm{Tr}\left\{I_x^{\mathit{†}}U{Q}_{zz}{U}^{\mathit{†}}\right\}}{\mathrm{Tr}\left\{I_x^{\mathrm{2}}\right\}}}.\end{array}\end{array}$$

In an ideal weakly coupled spin system, with infinitely short, ideal, radiofrequency pulses and delays given by ${\mathit{\tau }}_{\mathrm{3}}=|\mathit{\pi }/{\mathit{\omega }}_{\mathrm{\Delta }}|$ and ${\mathit{\tau }}_{\mathrm{4}}=\mathrm{1}/\left(\mathrm{4}J\right)$, the transformation amplitudes are as follows:

$$\begin{array}{}\text{(14)}& \begin{array}{rl}& a(\mathbf{SO}\to \mathbf{x})={\displaystyle \frac{\mathrm{2}}{\mathrm{3}}},\\ & a(\mathbf{zz}\to \mathbf{x})=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}.\end{array}\end{array}$$

These transformations are indicated by the red arrows and yellow boxes in Fig. 6.

The integrated amplitude of the NMR spectrum obtained by Fourier transformation of the NMR signal is therefore proportional to the zz and SO orders before the read-out sequence is applied, multiplied by the transformation factors in Eq. (14).

4.3 Analysis of experimental trajectories

The chemical kinetics and spin dynamics may be combined to achieve an understanding of the trajectories in Figs. 4 and 5 generated by the timing sequences shown in Fig. 3.

4.3.1 Trajectories with spin locking

The pulse sequences in Fig. 3a, b both examine the dependence of hyperpolarized signals on the duration τ₂ of a spin-locking interval. However, the state of the spin system at the start of the τ₂ interval is different in the two procedures. In Fig. 3a, which provides the results shown in Fig. 4, spin locking is applied continuously during the bubbling interval and continued during the variable delay τ₂. In the sequence of Fig. 3b, on the other hand, which provides the orange data points in Fig. 5, the spin locking is interrupted for 3 s before the τ₂ interval starts.

In both cases, the evolution of the singlet order during the spin-locking interval obeys the following differential equations:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)=-R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right),\\ & {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{C}_{\text{SO}}^{\mathbf{\text{I}}}\left(t\right)=+k{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)-R_{\mathrm{S}}^{\mathbf{\text{I}}}{C}_{\text{SO}}^{\mathbf{\text{I}}}\left(t\right),\end{array}\end{array}$$

The notation $C_{\text{SO}}^X\left(t\right)$ indicates the total amplitude of singlet spin order for the species X at time point t, taking into account the concentration of X as well as its spin state. The decay rate constant for singlet order in compound I, due to spin-dynamical processes, is denoted $R_{\mathrm{S}}^{\mathbf{\text{I}}}=T_{\text{S}}(\mathbf{\text{I}}{)}^{-\mathrm{1}}$. The total decay rate constant for H₂ singlet order, due to the combination of chemical and spin-dynamical processes, is denoted

$$\begin{array}{}\text{(16)}& R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}=k_{\mathrm{tot}}+R_{\mathrm{S}}^{{\mathrm{H}}_{\mathrm{2}}},\end{array}$$

where $R_{\mathrm{S}}^{{\mathrm{H}}_{\mathrm{2}}}$ denotes the decay rate constant for H₂ singlet order, due to para-to-ortho conversion in solution, in the presence of the hydrogenation catalyst but in the absence of a hydrogenation reaction. Note that this rate constant may be greatly increased by the presence of the catalyst, since transient binding of H₂ molecules with the catalyst provides an efficient mechanism for ortho–para conversion.

Equation (15) may be solved to obtain the following trajectory of the singlet order for compound I under spin locking:

$$\begin{array}{}\text{(17)}& C_{\text{SO}}^{\mathbf{\text{I}}}({\mathit{\tau }}_{\mathrm{2}},i)=A_i\exp \left\{-R_{\mathrm{S}}^{\mathbf{\text{I}}}{\mathit{\tau }}_{\mathrm{2}}\right\}+B_i\exp \left\{-R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{\mathrm{2}}\right\},\end{array}$$

where the coefficients are

$$\begin{array}{}\text{(18)}& \begin{array}{rl}& A_i=C_{\text{SO}}^{\mathbf{\text{I}}}(\mathrm{0},i)-B_i,\\ & B_i={\displaystyle \frac{k{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}(\mathrm{0},i)}{R_{\mathrm{S}}^{\mathbf{\text{I}}}-R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}}}.\end{array}\end{array}$$

The index i refers to the first two pulse sequences in Fig. 3, $i\in \mathit{\{}a,b\mathit{\}}$. The symbol $C_{\text{SO}}^{\mathbf{\text{I}}}(\mathrm{0},i)$ is the total amplitude of H₂ singlet order at the start of the spin-lock interval in experiment i, taking into account the concentration of I as well as its spin state.

The amplitude factor for the read-out of a singlet order is given by $(+\mathrm{2}/\mathrm{3})$, as shown by Eq. (14). Hence the integrated signal amplitudes for the sequences in Fig. 3a, b are given by

$$\begin{array}{}\text{(19)}& a_i\left({\mathit{\tau }}_{\mathrm{2}}\right)={\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{f}_i\left(A_i\exp \left\{-R_{\mathrm{S}}^{\mathbf{\text{I}}}{\mathit{\tau }}_{\mathrm{2}}\right\}+B_i\exp \left\{-R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{\mathrm{2}}\right\}\right),\end{array}$$

where f_i are instrumental factors and $i\in \mathit{\{}a,b\mathit{\}}$. The signal trajectories have a bi-exponential form, in general.

4.3.2 Trajectory without spin locking

The sequence in Fig. 3c is identical to that in Fig. 3b, except for the absence of the spin-locking field during the τ₂ interval. In the absence of spin locking, the relevant eigenoperator of the spin evolution during the τ₂ interval is the zz operator Q_zz (Eq. 9). The combined chemical–spin dynamics of the system is described by the following differential equations:

$$\begin{array}{}\text{(20)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)=-R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right),\\ & {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{C}_{zz}^{\mathbf{\text{I}}}\left(t\right)=(-{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}})k{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)-R_{zz}^{\mathbf{\text{I}}}{C}_{zz}^{\mathbf{\text{I}}}\left(t\right),\end{array}\end{array}$$

The factor $(-\mathrm{2}/\mathrm{3})$ appears since the H₂ singlet order is projected onto the zz order of the product molecule I upon hydrogenation, as described in Sect. 4.2.3. This equation is valid provided that the interval t exceeds the time required for dephasing of spin-order components orthogonal to zz order after hydrogenation in the absence of a spin-locking field.

The differential Eq. (20) may be solved to obtain the following trajectory for the zz order of compound I, under the pulse sequence of Fig. 3c:

$$\begin{array}{}\text{(21)}& C_{zz}^{\mathbf{\text{I}}}(t,c)=A_c\exp \left\{-R_{zz}^{\mathbf{\text{I}}}t\right\}+B_c\exp \left\{-R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}t\right\},\end{array}$$

where the coefficients are

$$\begin{array}{}\text{(22)}& \begin{array}{rl}& A_c=C_{zz}^{\mathbf{\text{I}}}(\mathrm{0},c)-B_c,\\ & B_c=-{\displaystyle \frac{\mathrm{2}k{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}(\mathrm{0},c)}{\mathrm{3}\left(R_{zz}^{\mathbf{\text{I}}}-R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}\right)}}.\end{array}\end{array}$$

Here $C_{zz}^{\mathbf{\text{I}}}(\mathrm{0},c)$ is the zz order of compound I at the beginning of the τ₂ interval. This equation assumes that t is longer than the time required for dephasing of spin-order components orthogonal to the singlet order, in the presence of the spin-locking field. The zz order at the end of the τ₂ interval is transformed into observable x magnetization by applying a sequence of two pulses and three delays. The amplitude factor for the read-out of zz order is given by $(-\mathrm{1}/\mathrm{2})$, as shown by Eq. (14). Hence the integrated signal amplitude for the sequence in Fig. 3c is proportional to

$$\begin{array}{}\text{(23)}& a_c\left({\mathit{\tau }}_{\mathrm{2}}\right)=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{f}_c\left(A_c\exp \left\{-R_{zz}^{\mathbf{\text{I}}}{\mathit{\tau }}_{\mathrm{2}}\right\}+B_c\exp \left\{-R_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{\mathrm{2}}\right\}\right).\end{array}$$

This also has the form of a bi-exponential decay.

Since the sequences in Fig. 3b and c are the same up to the start of the τ₂ interval (indicated by the star in the pulse-sequence diagrams), the instrumental factors are identical (f_b=f_c) and we can write

$$\begin{array}{}\text{(24)}& C_{\text{SO}}^{\mathbf{\text{I}}}(\mathrm{0},b)=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{C}_{zz}^{\mathbf{\text{I}}}(\mathrm{0},c)\end{array}$$

using the projection in Eq. (11). Hence the signal amplitudes for these two experiments have the following relationship when extrapolated back to the start of the τ₂ interval:

$$\begin{array}{}\text{(25)}& {\displaystyle \frac{{\mathit{\alpha }}_b\left(\mathrm{0}\right)}{{\mathit{\alpha }}_c\left(\mathrm{0}\right)}}={\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}.\end{array}$$

The difference in extrapolated starting points is evident in the theoretical curves shown by the solid lines in Fig. 5.

Since the procedures in Fig. 3b and c are identical for τ₂=0, one would expect α_b(0)=α_c(0), in contradiction to Eq. (25). This apparent paradox is resolved by noting that the derivation of Eq. (25) relies on the projections in Eqs. (10) and (11), which are not valid for very short intervals τ₂.

4.3.3 Data fitting

The data sets of Figs. 4 and 5 were fitted simultaneously using the set of global parameters. All three data sets were well fitted by the functions a_a(τ₂), a_b(τ₂), and a_c(τ₂) (Eqs. 19 and 23) with the following parameters: $T_{\mathrm{S}}^{\mathbf{\text{I}}}=\mathrm{151}\pm \mathrm{9}$ s; $T_{\mathrm{\Sigma }}^{{\mathrm{H}}_{\mathrm{2}}}=\mathrm{28.7}\pm \mathrm{3.8}$ s; $T_{zz}^{\mathbf{\text{I}}}=\mathrm{13.2}\pm \mathrm{1.3}$ s; $f_a{A}_a=\mathrm{1.79}\pm \mathrm{0.07}$; f_bB_a≈0; $f_b{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}(\mathrm{0},b)\times k=\mathrm{0.059}\pm \mathrm{0.007}{\mathrm{s}}^{-\mathrm{1}}$; $f_c{C}_{zz}^{\mathbf{\text{I}}}(\mathrm{0},c)=-\mathrm{1.2}\pm \mathrm{0.1}$. All rate constants are expressed here as time constants, i.e. $T_X=R_X^{-\mathrm{1}}$. The parameters $f_b{C}_{\text{SO}}^{{\mathrm{H}}_{\mathrm{2}}}(\mathrm{0},b)$ and k interact strongly in the fit and could not be determined independently. The coefficient of determination R² was estimated to be 0.991 for the fit in Fig. 4 and 0.925 and 0.966 for the fits of the build-up and decay curves in Fig. 5, respectively.

For these parameters, the trajectory in Fig. 4 is very close to a single-exponential decay with time constant $T_{\mathrm{S}}^{\mathbf{\text{I}}}=\mathrm{151}\pm \mathrm{9}$ s. For the case of the orange curve in Fig. 5, on the other hand, the singlet order on I starts at a relatively low level. The long singlet decay time constant allows accumulation of a singlet order as the reaction proceeds in the presence of the spin-locking field. This accumulation gives rise to the rising initial trajectory of the orange curve in Fig. 5. The comparatively short time constant for the decay of zz order, $T_{zz}^{\mathbf{\text{I}}}\simeq \mathrm{13.2}$ s, allows no time for zz order to accumulate in the absence of a spin-locking field, giving rise to the monotonically decaying blue curve in Fig. 5.

Table 1 Experimental procedure for gem-PHIP experiments.

The singlet decay time constant for the methylene protons of compound I was determined independently by non-hyperpolarized experiments (see Supplement). These experiments were performed at a much lower sample temperature of 295 K to avoid the decomposition of I. The estimated value of $T_{\mathrm{S}}^{\mathbf{\text{I}}}$ at 295 K and a magnetic field of 9.41 T is 61.1±7.1 s. This value is much shorter than the estimate of $T_{\mathrm{S}}^{\mathbf{\text{I}}}=\mathrm{151}\pm \mathrm{9}$ s from the hyperpolarization trajectories. The discrepancy may be due in part to a reduction in rotational correlation time for the molecules of I at the elevated temperature used in the PHIP experiments.

5 Materials and methods

All experiments were conducted on a Bruker Avance Neo 400 MHz (9.41 T) system equipped with a 5 mm BBO probe. The excitation pulses were applied on-resonance with the doublet at 3.6 to 3.7 ppm. Their amplitude corresponded to a nutation frequency of ∼20 kHz. The spectral width was set to 20 ppm with sampling of 65k points.

The reagent solution consisted of 100 mM disodium acetylenedicarboxylate and 6 mM [Cp^∗Ru(CH₃CN)₃]PF₆ dissolved in D₂O. All sample solutions were prepared by mixing the components, sonicating the mixture for 5 min at 50 ^∘C and filtering it through a 0.2 µm pore-size syringe filter with a nylon membrane.

Para-enriched hydrogen was produced by slowly passing hydrogen gas through an iron oxide catalyst submerged in liquid nitrogen to obtain 50 % para-enriched hydrogen. A container was pressurized with 10 bar of para-enriched H₂ to contain gas for a whole series of experiments at 4 bar of parahydrogen pressure.

Hydrogenation experiments of disodium acetylenedicarboxylate and catalyst [Cp^∗Ru(CH₃CN)₃]PF₆ were carried out strictly according to the experimental procedure in Table 1. For each experiment, a 300 µL aliquot was used from a stock solution. Bubbling was performed in a 5 mm Wilmad^® quick pressure valve NMR tube through a $\mathrm{1}/{\mathrm{16}}^{\prime \prime }$ PEEK capillary, using 4 bar parahydrogen pressure, 60 ^∘C (333 K) temperature, and a gas flow of 400 sccm.

Spin locking was performed by irradiating a continuous wave rf field at the mean resonance frequency of the CH₂ protons and with an amplitude corresponding to a 1.0 kHz nutation frequency.

6 Conclusions

In this work we have demonstrated geminal hydrogenation of a precursor molecule using para-enriched hydrogen gas. We show that singlet order for the methylene proton pair may be maintained by application of a spin-locking field and that the proton singlet order in the product molecule relaxes with the time constant $T_{\mathrm{S}}^{\mathbf{\text{I}}}\simeq \mathrm{151}$ s, which is more than 50 times T₁. We have developed a simplified kinetic model to describe the time dependence of the hyperpolarized signals observed in such experiments, which include the chemical kinetics as well as the spin dynamics. This allows simultaneous fitting of the data from several experiments and estimation of most of the kinetic parameters and relaxation rate constants.

The particular hydrogenation reaction discussed here does not lead to a product molecule with a biological function. Nevertheless, our results demonstrate the principle of methylene hyperpolarization by hydrogenative PHIP and that the short T₁ values of these protons do not necessarily prevent the accumulation of hyperpolarization. We hope that this work might allow exploration of a new range of hyperpolarized molecular targets.

Appendix A: ¹H NMR spectrum of the reaction solution

The ¹H NMR spectrum of the reaction solution, together with peak assignments, is given in Fig. A1.

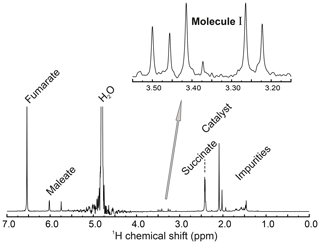
Figure A1 Full ¹H NMR spectrum (400 MHz) of the reaction solution after hydrogenation, taken at a temperature of 298 K. An expanded view of the methylene region is shown. This shows four peaks from the inequivalent methylene protons of the reaction product I as well as an additional peak at 3.50 ppm from the achiral decomposition product of I (see Supplement). The small peak at 3.37 ppm is unassigned. The spectrum shows peaks from several other substances, including fumarate, succinate, and maleate, as well as the hydrogenation catalyst.

Appendix B: Partially relaxed hyperpolarized spectra

Figure 2 shows two ¹H NMR spectra. The first was taken immediately after a PHIP experiment, while the second was taken after waiting for an interval of 90 s after the PHIP experiment. A minor asymmetry in the “roof effect” pattern of line amplitudes may be seen in the latter spectrum. An explanation of this observation is provided below.

The coherent spin Hamiltonian for a system of two chemically inequivalent protons may be written as follows:

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}& {\mathcal{H}}_{\mathrm{coh}}={\mathit{\omega }}_{\mathrm{\Delta }}\left(I_{\mathrm{1}z}-I_{\mathrm{2}z}\right)+\mathrm{2}\mathit{\pi }J{\mathbf{I}}_{\mathrm{1}}\cdot {\mathbf{I}}_{\mathrm{2}},\\ & {\mathit{\omega }}_{\mathrm{\Delta }}=-{\mathit{\gamma }}_H{B}_{\mathrm{0}}\left({\mathit{\delta }}_{\mathrm{1}}-{\mathit{\delta }}_{\mathrm{2}}\right).\end{array}\end{array}$$

This Hamiltonian is expressed in a rotating frame at the mean resonance frequency of the two spins. The parameters for numerical simulations were set to J=16.9 Hz and ${\mathit{\omega }}_{\mathrm{\Delta }}/\mathrm{2}\mathit{\pi }=\mathrm{80}$ Hz. Numerical simulations were performed using SpinDynamica software (Bengs and Levitt, 2018).

Two different initial density matrices were considered: (1) ρ₁=I_z, corresponding to longitudinal magnetization, neglecting the unity operator and numerical factors for simplicity. (2) The definition of the second density operator is more complex. The reaction with para-enriched hydrogen deposits proton singlet order in the reaction product which evolves under the Hamiltonian of the new system. Since the singlet order is not an eigenoperator of the spin evolution, a secular approximation must be applied. This omits any coherences created by instant projection of the singlet order onto the Hamiltonian eigenbasis. Thus, the second density matrix ρ₂ corresponds to the singlet order of the two protons secularized according to the Hamiltonian in Eq. (B1), with the coupling and chemical shift values given above.

A strong π∕2 pulse excites very different spectra for the two initial density operators. The first spectrum displays a distinct “roof effect” for the peak amplitudes, whereas the second spectrum displays an alternating peak pattern, typical for parahydrogen-enhanced NMR (Bowers and Weitekamp, 1987). If the sample contains a fully relaxed spin ensemble together with a similar amount of singlet order originating from a previous parahydrogen reaction, the total spectrum is a superposition of the two different patterns (see Fig. B1). This gives a good match to the experimental spectrum in Fig. 2.

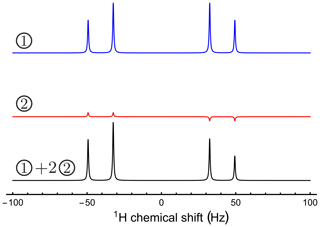
Figure B1 The origin of the asymmetry observed in Fig. 2. The simulated spectra show signals generated by two different density operators, excited by an identical π∕2 pulse. The first initial state corresponds to pure longitudinal magnetization. The second initial state corresponds to a singlet order secularized under the Hamiltonian given in Eq. (B1). A suitably weighted superposition of the two spectra is a good match to the experimental spectrum.