Hyperpolarization and the physical boundary of Liouville space

The quantum state of a spin ensemble is described by a density operator, which corresponds to a point in the Liouville space of orthogonal spin operators. Valid density operators are confined to a particular region of Liouville space, which we call the physical region and which is bounded by multidimensional figures called simplexes. Each vertex of a simplex corresponds to a pure-state density operator. We provide examples for spins $I=\mathrm{1}/\mathrm{2}$, I=1, $I=\mathrm{3}/\mathrm{2}$ and for coupled pairs of spins-1/2. We use the von Neumann entropy as a criterion for hyperpolarization. It is shown that the inhomogeneous master equation for spin dynamics leads to non-physical results in some cases, a problem that may be avoided by using the Lindbladian master equation.

1 Introduction

The central object of interest in nuclear magnetic resonance (NMR) theory is the density operator, which describes the quantum state of the ensemble of spin systems. It is defined as follows:

$$\begin{array}{}\text{(1)}& \mathit{\rho }=\stackrel{\mathrm{‾}}{\mathrm{|}\mathit{\psi }\rangle \langle \mathit{\psi }\mathrm{|}}.\end{array}$$

Here |ψ〉 specifies the quantum state of each individual spin system, and the overbar indicates an ensemble average (Ernst et al., 1987). When expressed as a matrix in the eigenbasis of the coherent spin Hamiltonian, the diagonal elements are the spin state populations, and the off-diagonal elements are the coherences between the spin states.

It is often useful to express the density operator as a superposition of orthogonal spin operators. For example, the highly influential papers by Sørensen, Bodenhausen, Ernst and co-workers advocate an expansion in terms of Cartesian product operators (Sørensen et al., 1984; Ernst et al., 1987), while some other groups favour spherical tensor operators (Sanctuary, 1976, 1980; Sanctuary and Temme, 1985a, b; Bowden and Hutchison, 1986b; Bowden et al., 1986; Bowden and Hutchison, 1986a, 1987; Bowden et al., 1990; Bain, 1978, 1980a, b; Philp and Kuchel, 2005; Garon et al., 2015). In all cases, the density operator is written in the form

$$\begin{array}{}\text{(2)}& \mathit{\rho }=\sum _{q=\mathrm{1}}^{N_L}{\mathit{\rho }}_q{Q}_q,\end{array}$$

where the coefficients ρ_q are complex numbers in general, and the basis operators Q_q are orthogonal:

$$\begin{array}{}\text{(3)}& \left(Q_q\mathrm{|}{Q}_{q^{\prime }}\right)=\text{Tr}\mathit{\left\{}{Q}_q^{†}{Q}_{q^{\prime }}\mathit{\right\}}={\mathit{\delta }}_{q{q}^{\prime }}\Vert Q_q{\Vert }^{\mathrm{2}}.\end{array}$$

The Kronecker delta symbol δ_ab takes the value 1 for a=b and 0 otherwise. The norm of the operator Q_q is defined as $\Vert Q_q\Vert =\text{Tr}\mathit{\left\{}{Q}_q^{†}{Q_q}^{\mathrm{1}/\mathrm{2}}\mathit{\right\}}$.

The coefficients ρ_q are often given evocative names which suggest their physical interpretation, for example “antiphase order”, “zz order”, “spin alignment”, “Zeeman polarization”, ”singlet order”, and so on.

Since such expansions are nearly universal in modern NMR theory, it seems natural to pose questions of the forms “what values may the coefficients ρ_q take?”, “are the values of ρ_q unlimited, or bounded in some way?”, “does the value of one coefficient influence the possible values of a second coefficient?”, etc. Surprisingly, these natural questions are rarely posed in the NMR world, although they have not escaped the attention of mathematical physicists and applied mathematicians (Byrd and Khaneja, 2003; Kimura and Kossakowski, 2005; Bengtsson and Zyczkowski, 2006; Goyal et al., 2016; Szymański et al., 2018).

The expansion in Eq. (2) identifies the density operator with a point in a multidimensional space with coordinates {ρ₁,ρ₂…}. This space has been called Liouville space (Banwell and Primas, 1963; Suzuki and Kubo, 1964; Ernst et al., 1987). In this article, we show that valid density operators may only be identified with points in a defined region of Liouville space which we call the physical region. The physical region is enclosed by a convex boundary, which we call the physical boundary of Liouville space. We ask: what is the shape of the physical boundary? Does it have straight edges, or is it spherical in all dimensions? (Spoiler: at least some edges are straight.)

In addition, we express some views on the nature and definition of hyperpolarization. For example, is pure parahydrogen hyperpolarized, even though it generates no NMR signal? (Spoiler: our answer is yes.)

2 Orthonormal operators

To facilitate the discussion, the basis operators Q_q in Eq. (2) are henceforth considered to be normalized as well as orthogonal, so that Eq. (3) is replaced by the simpler form

$$\begin{array}{}\text{(4)}& \left(Q_q\mathrm{|}{Q}_{q^{\prime }}\right)=\text{Tr}\mathit{\left\{}{Q}_q^{†}{Q}_{q^{\prime }}\mathit{\right\}}={\mathit{\delta }}_{q{q}^{\prime }}.\end{array}$$

Note, however, that the Cartesian product operators advocated by Sørensen et al. (1984) are not normalized.

In general, N_L operators are required in the expansion of Eq. (2), where $N_L=N_H^{\mathrm{2}}$ and N_H is the dimension of the Hilbert space of the individual spin systems. The orthonormal operators $\mathit{\{}{Q}_{\mathrm{1}},Q_{\mathrm{2}}\mathrm{\dots }{Q}_{N_L}\mathit{\}}$ define a N_L-dimensional Liouville space (Jeener, 1982; Ernst et al., 1987). The density operator may be represented as a point with coordinates $\mathit{\{}{q}_{\mathrm{1}},q_{\mathrm{2}}\mathrm{\dots }{q}_{N_L}\mathit{\}}$ in this space. All spin dynamics may be represented as a trajectory traced by the spin density operator as it moves through this abstract space.

Brief consideration shows that there must be limits to the physical region of Liouville space. Consider for example an ensemble of isolated spins-1/2. In this case, the dimension of Hilbert space is N_H=2, and the dimension of Liouville space is N_L=4. The following four normalized operators may be chosen as the basis of Liouville space:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{Q}_{\mathrm{1}}={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}\mathbb{I}& Q_{\mathrm{2}}={\mathrm{2}}^{\mathrm{1}/\mathrm{2}}{I}_x\\ Q_{\mathrm{3}}={\mathrm{2}}^{\mathrm{1}/\mathrm{2}}{I}_y& Q_{\mathrm{4}}={\mathrm{2}}^{\mathrm{1}/\mathrm{2}}{I}_z\end{array}\end{array}$$

Since Tr{ρ}=1 by definition, the first coefficient is fixed at $q_{\mathrm{1}}={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}$, the density operator is only free to move in the subspace formed by the other three operators, $\mathit{\{}{Q}_{\mathrm{2}},Q_{\mathrm{3}},Q_{\mathrm{4}}\mathit{\}}$, which are proportional to the angular momentum operators in the three Cartesian directions.

The populations of the two Zeeman states are given by

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\langle \mathit{\alpha }\mathrm{|}\mathit{\rho }\mathrm{|}\mathit{\alpha }\rangle & ={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}(q_{\mathrm{1}}+q_{\mathrm{4}})\\ \langle \mathit{\beta }\mathrm{|}\mathit{\rho }\mathrm{|}\mathit{\beta }\rangle & ={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}(q_{\mathrm{1}}-q_{\mathrm{4}})\end{array}\end{array}$$

Both state populations are, by definition, bounded by 0 and 1:

$$\begin{array}{}\text{(7)}& \begin{array}{r}\mathrm{0}\le \langle \mathit{\alpha }\mathrm{|}\mathit{\rho }\mathrm{|}\mathit{\alpha }\rangle \le \mathrm{1}\\ \mathrm{0}\le \langle \mathit{\beta }\mathrm{|}\mathit{\rho }\mathrm{|}\mathit{\beta }\rangle \le \mathrm{1}\end{array}\end{array}$$

Hence the coefficient q₄ is bounded as follows:

$$\begin{array}{}\text{(8)}& -{\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}\le q_{\mathrm{4}}\le {\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}.\end{array}$$

The upper bound $q_{\mathrm{4}}={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}$ corresponds to maximum spin polarization along the positive z axis, with the |α〉 state completely populated and the |β〉 state completely depleted. The lower bound $q_{\mathrm{4}}=-{\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}$ corresponds to maximum spin polarization along the negative z axis, with the |α〉 state completely depleted and the |β〉 state completely populated.

In the case of isolated spins-1/2, the physical bounds on Liouville space are therefore defined by the fixing of one coordinate ($q_{\mathrm{1}}={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}$) and the constraint of the other three to the interior of a sphere of radius ${\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}$. Within a numerical factor, this geometrical bound is of course identical to the familiar Bloch sphere – the seminal geometrical object in magnetic resonance theory.

What about systems other than spins-1/2? Liouville space has more than three dimensions in such cases and is hard to visualize. Nevertheless, it is tempting to assume that the physical bounds are still spherical, albeit with an extension to higher dimensions. However, this turns out to be incorrect, in general. The physical bounds in some of the dimensions of Liouville space turn out not to be spheres but regular simplexes. A regular simplex in one dimension is a line, a regular simplex in two dimensions is an equilateral triangle, and a regular simplex in three dimensions is a regular tetrahedron, with the concept extending to arbitrary dimensions. In general, a simplex is the simplest possible convex object, where the term convex means that any two points belonging to the object may be connected by a straight line which never leaves the object. In general, a simplex in N dimensions is called an N-simplex, although some simplexes also have special names, such as the line (1-simplex), the triangle (2-simplex), the tetrahedron (3-simplex), and the pentachoron or 5-cell (4-simplex) (Coxeter, 1963).

The physical boundary of Liouville space is of little consequence for “conventional” NMR experiments, which are performed at or near thermal equilibrium. Under ordinary temperatures and magnetic fields, this is a region very close to the origin of Liouville space (except for the fixed projection onto the unity operator) and hence very far from the boundary. However, hyperpolarization techniques such as optical pumping (Kastler, 1957; Navon et al., 1996), dynamic nuclear polarization (Griffin and Prisner, 2010; Ardenkjaer-Larsen et al., 2003; Jannin et al., 2012), quantum-rotor-induced polarization (Icker and Berger, 2012; Meier et al., 2013; Dumez et al., 2015) and parahydrogen-induced polarization (Bowers and Weitekamp, 1987; Adams et al., 2009) have provided ready access to regions which are “close to the edge”. Furthermore, spin systems which are in a highly non-equilibrium state are of great practical importance because of the greatly enhanced NMR signals that they can produce. The position and shape of the physical boundary have therefore become relevant.

Furthermore, some familiar concepts in magnetic resonance which were originally developed in the context of near-equilibrium spin dynamics do not retain validity far from the origin. An important case is the inhomogeneous master equation (Ernst et al., 1987), which fails close to the physical boundary of Liouville space, where it should be replaced by a Lindbladian master equation (Bengs and Levitt, 2020; Pell, 2021).

3 Polarization moments

3.1 Isolated spins-I

For an ensemble of isolated spins-I, a suitable expansion of the form in Eq. (2) is as follows:

$$\begin{array}{}\text{(9)}& \mathit{\rho }=\sum _{\mathit{\lambda }=\mathrm{0}}^{\mathrm{2}I}\sum _{\mathit{\mu }=-I}^{+I}{\mathit{\rho }}_{\mathit{\lambda }\mathit{\mu }}{\mathbb{T}}_{\mathit{\lambda }\mathit{\mu }}.\end{array}$$

Here ρ_λμ are complex numbers which are called here polarization moments, following the usage in the atomic physics community (Budker et al., 2002; Auzinsh et al., 2014). The operators 𝕋_λμ are normalized irreducible spherical tensor operators (NISTOs). They are normalized over the spin-I Hilbert space:

$$\begin{array}{}\text{(10)}& \left({\mathbb{T}}_{\mathit{\lambda }\mathit{\mu }}\mathrm{|}{\mathbb{T}}_{\mathit{\lambda }\mathit{\mu }}\right)=\text{Tr}\mathit{\left\{}{\mathbb{T}}_{\mathit{\lambda }\mathit{\mu }}^{{}^{†}}{\mathbb{T}}_{\mathit{\lambda }\mathit{\mu }}\mathit{\right\}}=\mathrm{1}.\end{array}$$

The normalized spherical tensor operators 𝕋_λμ differ from the operators T_λμ commonly used in NMR theory (Spiess, 1978; Mehring, 1976) by a multiplicative factor.

A semantic objection may be raised over the use of the term polarization moment for the case λ=0. The term polarization is generally taken to imply an anisotropic distribution of dipole moments (magnetic or electric). However, the rank-0 moment represents an isotropic distribution of spin angular momentum and hence is not a “polarization” in a conventional sense. While acknowledging that this is a reasonable objection, we contend that the extension of the term “polarization” to cover rank-0 terms is too convenient to be blocked by pedantry. A similar objection arises over the term singlet polarization for spin pairs, as discussed below.

For isolated spins-I, the low-rank normalized spherical tensor operators are as follows, for the case μ=0:

$$\begin{array}{}\text{(11)}& \begin{array}{rl}{\mathbb{T}}_{\mathrm{00}}& ={\mathbb{N}}_{\mathrm{0}}^I\mathbb{I}\\ {\mathbb{T}}_{\mathrm{10}}& ={\mathbb{N}}_{\mathrm{1}}^I{I}_z\\ {\mathbb{T}}_{\mathrm{20}}& ={\mathbb{N}}_{\mathrm{2}}^I{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{6}}}}(\mathrm{3}{I_z}^{\mathrm{2}}-I(I+\mathrm{1}\left)\mathbb{I}\right)\\ {\mathbb{T}}_{\mathrm{30}}& ={\mathbb{N}}_{\mathrm{3}}^I{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{10}}}}(\mathrm{5}{I_z}^{\mathrm{3}}+(\mathrm{1}-\mathrm{3}I(I+\mathrm{1})\left)I_z\right)\end{array}\end{array}$$

The normalization factors are as follows:

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{\mathbb{N}}_{\mathrm{0}}^I& =(\mathrm{2}I+\mathrm{1}{)}^{-\mathrm{1}/\mathrm{2}}\\ {\mathbb{N}}_{\mathrm{1}}^I& =\mathit{\left\{}{\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}I\right(I+\mathrm{1}\left)\right(\mathrm{2}I+\mathrm{1}){\mathit{\}}}^{-\mathrm{1}/\mathrm{2}}\\ {\mathbb{N}}_{\mathrm{2}}^I& =\mathit{\left\{}{\displaystyle \frac{\mathrm{1}}{\mathrm{30}}}I\right(I+\mathrm{1}\left)\right(\mathrm{2}I-\mathrm{1}\left)\right(\mathrm{2}I+\mathrm{3}\left)\right(\mathrm{2}I+\mathrm{1}){\mathit{\}}}^{-\mathrm{1}/\mathrm{2}}\\ {\mathbb{N}}_{\mathrm{3}}^I& =\mathit{\left\{}{\displaystyle \frac{\mathrm{1}}{\mathrm{70}}}I\right(I+\mathrm{1}\left)\right(I-\mathrm{1}\left)\right(I+\mathrm{2}\left)\right(\mathrm{2}I-\mathrm{1})\\ & \times (\mathrm{2}I+\mathrm{3})(\mathrm{2}I+\mathrm{1}){\mathit{\}}}^{-\mathrm{1}/\mathrm{2}}\end{array}\end{array}$$

These normalization factors depend on the spin quantum number I and the rank λ but are independent of the component index μ.

It follows from Eqs. (2) and (10) and the orthogonality of the NISTOs that any polarization moment may be derived from the density operator by a Liouville bracket operation:

$$\begin{array}{}\text{(13)}& {\mathit{\rho }}_{\mathit{\lambda }\mathit{\mu }}=\left({\mathbb{T}}_{\mathit{\lambda }\mathit{\mu }}\mathrm{|}\mathit{\rho }\right)=\text{Tr}\mathit{\left\{}{\mathbb{T}}_{\mathit{\lambda }\mathit{\mu }}^{{}^{†}}\mathit{\rho }\mathit{\right\}}.\end{array}$$

The polarization moments have the following symmetry:

$$\begin{array}{}\text{(14)}& {\mathit{\rho }}_{\mathit{\lambda }\mathit{\mu }}=(-\mathrm{1}{)}^{-\mathit{\mu }}{\mathit{\rho }}_{\mathit{\lambda }-\mathit{\mu }}^{*},\end{array}$$

which follows from the hermiticity of the density operator and the symmetries of the spherical tensor operator components (Varshalovich et al., 1988).

For isolated spins-I, the condition Tr{ρ}=1 fixes the value of the rank-0 polarization moment:

$$\begin{array}{}\text{(15)}& {\mathit{\rho }}_{\mathrm{00}}=(\mathrm{2}I+\mathrm{1}{)}^{-\mathrm{1}/\mathrm{2}}.\end{array}$$

The rank-1 polarization moment ρ₁₀ is proportional to the z polarization of the spin-I ensemble as follows:

$$\begin{array}{}\text{(16)}& {\mathit{\rho }}_{\mathrm{10}}=\mathit{\left\{}{\displaystyle \frac{\mathrm{1}}{\mathrm{3}I}}\right(I+\mathrm{1}\left)\right(\mathrm{2}I+\mathrm{1}){\mathit{\}}}^{-\mathrm{1}/\mathrm{2}}{p}_z.\end{array}$$

Similarly, the rank-1 polarization moments ρ_1±1 are proportional to complex combinations of the transverse polarizations:

$$\begin{array}{}\text{(17)}& {\mathit{\rho }}_{\mathrm{1}\pm \mathrm{1}}=\mathit{\left\{}{\displaystyle \frac{\mathrm{2}}{\mathrm{3}I}}\right(I+\mathrm{1}\left)\right(\mathrm{2}I+\mathrm{1}\left){\mathit{\}}}^{-\mathrm{1}/\mathrm{2}}\right(\mp p_x+i{p}_y).\end{array}$$

The relationship in Eq. (16) evaluates as follows for some common spin quantum numbers I:

$$\begin{array}{}\text{(18)}& \begin{array}{rl}{\mathit{\rho }}_{\mathrm{10}}={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}{p}_z& \text{(}I=\mathrm{1}/\mathrm{2}\text{)}\\ {\mathit{\rho }}_{\mathrm{10}}={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}{p}_z& \text{(}I=\mathrm{1}\text{)}\\ {\mathit{\rho }}_{\mathrm{10}}={\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}{\mathrm{5}}^{-\mathrm{1}/\mathrm{2}}{p}_z& \text{(}I=\mathrm{3}/\mathrm{2}\text{)}\\ {\mathit{\rho }}_{\mathrm{10}}=({\displaystyle \frac{\mathrm{5}}{\mathrm{14}}}{)}^{\mathrm{1}/\mathrm{2}}{p}_z& \text{(}I=\mathrm{5}/\mathrm{2}\text{)}\end{array}\end{array}$$

In atomic physics, finite moments with rank λ=1 are called orientation, while finite moments with rank λ=2 are called alignment (Auzinsh et al., 2014). Although the term orientation is not generally used for this purpose in the magnetic resonance community, the term alignment is used to imply rank-2 multipole order, particularly in the context of solid-state NMR as applied to quadrupolar nuclei (Batchelder, 2007). For isolated spins-I, the terms spin alignment and quadrupolar order may be regarded as synonymous.

Multipole expansions of the spin density operator as in Eq. (2) have long been used in NMR. Extensive theoretical development was performed by Sanctuary, Bowden, Bain and co-workers (Sanctuary, 1976, 1980; Sanctuary and Temme, 1985a, b; Bowden and Hutchison, 1986b; Bowden et al., 1986; Bowden and Hutchison, 1986a; Bowden et al., 1990; Bain, 1978, 1980a, b) and has been exploited to generate graphical representations of density operator evolution (Philp and Kuchel, 2005; Garon et al., 2015). One of the salient early examples of the multipole description is the treatment of quadrupolar relaxation by Bodenhausen and co-workers (Jaccard et al., 1986). In this elegant paper, the relaxation dynamics of quadrupolar nuclei outside the extreme narrowing limit is treated in terms of propagation in the space of spherical tensor operators, drawing fruitful parallels with the concepts of coherence transfer pathways (Bodenhausen et al., 1984; Bain, 1984).

There are also techniques for determining the polarization moments of a spin ensemble experimentally at any point during a pulse sequence by combining the signals from many successive experiments multiplied by complex factors. This method has been called spherical tensor analysis (van Beek et al., 2005) and has been applied to the study of endofullerenes (Carravetta et al., 2007).

3.2 Spin-1/2 pairs

The construction of spherical tensor operators for systems of coupled spins is a complicated affair. Extensive expositions of the technique have been given (Sanctuary, 1976, 1980; Sanctuary and Temme, 1985a, b; Bowden et al., 1990; Garon et al., 2015). In this article, the discussion of coupled spin systems is restricted to the simplest case, namely pairs of coupled spins-1/2. Since the dimension of Hilbert space is N_H=4, the dimension of Liouville space is N_L=16. This space includes six orthogonal zero-quantum operators, four of which are symmetric with respect to spin exchange and two of which are antisymmetric. The four symmetric μ=0 operators are as follows:

$$\begin{array}{}\text{(19)}& \begin{array}{rl}{\mathbb{T}}_{\mathrm{00}}^{\mathrm{0}}& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathbb{I},\\ {\mathbb{T}}_{\mathrm{00}}^{\mathrm{12}}& =-\mathrm{2}\times {\mathrm{3}}^{-\mathrm{1}/\mathrm{2}}{\mathbf{I}}_{\mathrm{1}}\cdot {\mathbf{I}}_{\mathrm{2}},\\ {\mathbb{T}}_{\mathrm{10}}^{+}& ={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}(I_{\mathrm{1}z}+I_{\mathrm{2}z}),\\ {\mathbb{T}}_{\mathrm{20}}^{\mathrm{12}}& =(\mathrm{2}/\mathrm{3}{)}^{\mathrm{1}/\mathrm{2}}(\mathrm{3}{I}_{\mathrm{1}z}{I}_{\mathrm{2}z}-{\mathbf{I}}_{\mathrm{1}}\cdot {\mathbf{I}}_{\mathrm{2}}).\end{array}\end{array}$$

Note that spin-1/2 pairs support two different spherical tensor operators with rank λ=0, denoted ${\mathbb{T}}_{\mathrm{00}}^{\mathrm{0}}$ and ${\mathbb{T}}_{\mathrm{00}}^{\mathrm{12}}$. The plus superscript in ${\mathbb{T}}_{\mathrm{10}}^{+}$ indicates that the operators I_1z and I_2z are combined with the same sign.

The operator ${\mathbb{T}}_{\mathrm{00}}^{\mathrm{0}}$ is proportional to the unity operator. The corresponding polarization moment is fixed by the condition Tr{ρ}=1 to the value

$$\begin{array}{}\text{(20)}& {\mathit{\rho }}_{\mathrm{00}}^{\mathrm{0}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

The operator ${\mathbb{T}}_{\mathrm{00}}^{\mathrm{12}}$ is proportional to the scalar product of the two spin angular momenta. The corresponding polarization moment is given by

$$\begin{array}{}\text{(21)}& {\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}}={\displaystyle \frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{p}_{\mathrm{S}},\end{array}$$

where p_S is called the singlet polarization or singlet order and corresponds to the population imbalance between the singlet state and the triplet manifold, in the spin-pair ensemble. In many cases, the singlet polarization is protected against common relaxation mechanisms and exhibits an extended lifetime (Carravetta et al., 2004; Carravetta and Levitt, 2004; Cavadini et al., 2005; Sarkar et al., 2007b, a; Ahuja et al., 2009; Levitt, 2019; Dumez, 2019).

Since the moments ${\mathit{\rho }}_{\mathrm{00}}^{\mathrm{0}}$ and ${\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}}$ have spherical rank λ=0, they both represent isotropic distributions of the spin angular momenta. As before, we contend that the extension of the term “polarization” to cover rank-0 spherical moments is too convenient to ignore while accepting that opinions may differ on the wisdom of this approach.

The operator ${\mathbb{T}}_{\mathrm{10}}^{+}$ corresponds to a symmetric combination of the z-angular momentum operators for the two spins. The corresponding polarization moment is proportional to the mean z polarization of the spin ensemble:

$$\begin{array}{}\text{(22)}& {\mathit{\rho }}_{\mathrm{10}}^{+}={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}{p}_z.\end{array}$$

The operator ${\mathbb{T}}_{\mathrm{20}}^{\mathrm{12}}$ corresponds to the rank-2 spherical tensor operator of the coupled spin pair. The corresponding polarization moment ${\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}}$ is proportional to the rank-2 order (dipolar order) of the spin-pair ensemble.

4 Physical bounds of Liouville space

The population of each individual spin state is bounded by 0 and 1, while the sum of all populations is equal to 1. These properties constrain the physically realizable values of the polarization moments.

The spin density operator of the isolated spin-I ensemble may be expressed as a superposition of spherical tensor operators, with rank λ taking values between 0 and 2I. The rank-0 moment is fixed to the value ${\mathit{\rho }}_{\mathrm{00}}=(\mathrm{2}I+\mathrm{1}{)}^{-\mathrm{1}}$ (Eq. 15). From Eq. (2) and the orthonormality of the NISTOs (Eq. 10), the population of the state |I,M_I〉 may be written as follows:

$$\begin{array}{}\text{(23)}& \langle I,M_I\mathrm{|}\mathit{\rho }\mathrm{|}I,M_I\rangle =\sum _{\mathit{\lambda }=\mathrm{0}}^{\mathrm{2}I}\langle I,M_I\mathrm{|}{\mathbb{T}}_{\mathit{\lambda }\mathrm{0}}\mathrm{|}I,M_I\rangle {\mathit{\rho }}_{\mathit{\lambda }\mathrm{0}}.\end{array}$$

Hence, for isolated spins-I, there exists a system of 2I+1 simultaneous inequalities on the μ=0 polarization moments:

$$\begin{array}{}\text{(24)}& \mathrm{0}\le \sum _{\mathit{\lambda }=\mathrm{0}}^{\mathrm{2}I}\langle I,M_I\mathrm{|}{\mathbb{T}}_{\mathit{\lambda }\mathrm{0}}\mathrm{|}I,M_I\rangle {\mathit{\rho }}_{\mathit{\lambda }\mathrm{0}}\le \mathrm{1},\end{array}$$

for $M_I\in \mathit{\{}+I,+I-\mathrm{1}\mathrm{\dots }-I\mathit{\}}$. Together with Eq. (15), the system of inequalities in Eq. (24) defines the physical bounds of the μ=0 polarization moments.

The consequences are now explored for some common spin systems.

4.1 Spins-1/2

For isolated spins-1/2, the rank-0 polarization moment is given from Eq. (15) by

$$\begin{array}{}\text{(25)}& {\mathit{\rho }}_{\mathrm{00}}={\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}\text{for}I=\mathrm{1}/\mathrm{2}.\end{array}$$

Equations (24) and (25) lead to the following physical bounds for the rank-1 polarization moment:

$$\begin{array}{}\text{(26)}& -{\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}\le {\mathit{\rho }}_{\mathrm{10}}\le +{\mathrm{2}}^{-\mathrm{1}/\mathrm{2}}\text{for}I=\mathrm{1}/\mathrm{2}.\end{array}$$

From Eq. (16), this corresponds to the expected bounds on the z polarization of the spin ensemble:

$$\begin{array}{}\text{(27)}& -\mathrm{1}\le p_z\le +\mathrm{1},\end{array}$$

which should come as no surprise. No spin system may have more than 100 % polarization.

4.2 Spins-1

The bounds on the polarization moments are more complicated for an ensemble of isolated spins-1. The rank-0 polarization moment is given through Eq. (15) by

$$\begin{array}{}\text{(28)}& {\mathit{\rho }}_{\mathrm{00}}={\mathrm{3}}^{-\mathrm{1}/\mathrm{2}}\text{for}I=\mathrm{1}.\end{array}$$

The inequalities on the rank-1 and rank-2 polarization moments evaluate as follows:

$$\begin{array}{}\text{(29)}& \begin{array}{rl}\mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}+{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}{\mathit{\rho }}_{\mathrm{10}}+{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{6}}}}{\mathit{\rho }}_{\mathrm{20}}\le \mathrm{1},\\ \mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}-\sqrt{{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}}{\mathit{\rho }}_{\mathrm{20}}\le \mathrm{1},\\ \mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}-{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}{\mathit{\rho }}_{\mathrm{10}}+{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{6}}}}{\mathit{\rho }}_{\mathrm{20}}\le \mathrm{1}\text{for}I=\mathrm{1}.\end{array}\end{array}$$

The values of {ρ₁₀,ρ₂₀} which satisfy the inequalities in Eq. (29) lie within the shaded triangle in Fig. 1. The vertices of the triangle have coordinates {ρ₁₀,ρ₂₀} given by $\mathit{\{}\pm {\mathrm{2}}^{-\mathrm{1}/\mathrm{2}},{\mathrm{6}}^{-\mathrm{1}/\mathrm{2}}\mathit{\}}$ and $\mathit{\{}\mathrm{0},-(\mathrm{2}/\mathrm{3}{)}^{\mathrm{1}/\mathrm{2}}\mathit{\}}$; each vertex corresponds to a pure-state density operator, in which only one state is populated. Similar triangular bounds have been identified in the mathematics literature (Kimura and Kossakowski, 2005; Goyal et al., 2016).

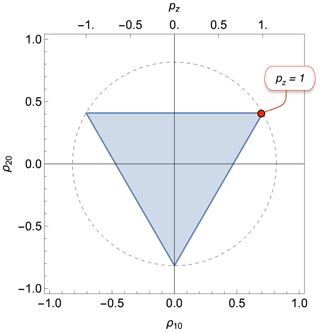
Figure 1 Physical bounds on the rank-1 and rank-2 polarization moments for isolated spins I=1. The shaded triangle shows the physically accessible region. The vertices correspond to pure-state density operators for each of the three spin-1 Zeeman states. The radius of the dashed circle is $\sqrt{\mathrm{2}/\mathrm{3}}$. The rank-1 polarization moment ρ₁₀ is related to the z polarization p_z through Eq. (18). The red circle indicates a state with maximum Zeeman polarization.

The equilateral triangle in Fig. 1 corresponds to a regular simplex in two dimensions.

The maximum z polarization of p_z=1 corresponds to the upper-right vertex. Figure 1 shows that this highly polarized state corresponds to a mixture of rank-1 polarization (Zeeman order) and rank-2 polarization (quadrupolar order). It follows that the near-complete hyperpolarization of spin-1 nuclei, as performed by the Bodenhausen group (Aghelnejad et al., 2020), generates hyperpolarized quadrupolar order as well as Zeeman order.

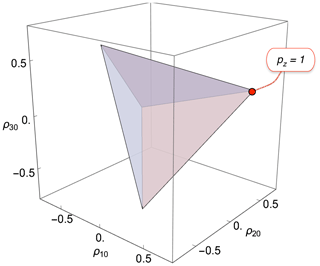
Figure 2 Physical bounds on the rank-1, rank-2, rank-3 polarization moments for isolated spins $I=\mathrm{3}/\mathrm{2}$. The shaded tetrahedron shows the physically accessible region. The vertices correspond to pure-state density operators for each of the four spin-1 Zeeman states. The red circle indicates the position of maximum Zeeman polarization.

4.3 Spins-3/2

In the case of isolated spins-3/2, the rank-0 polarization moment is given by

$$\begin{array}{}\text{(30)}& {\mathit{\rho }}_{\mathrm{00}}={\mathrm{4}}^{-\mathrm{1}/\mathrm{2}}=\mathrm{1}/\mathrm{2}\text{for}I=\mathrm{3}/\mathrm{2}.\end{array}$$

For spins-3/2, there may be a finite rank-3 polarization moment ρ₃₀ as well as the rank-1 and rank-2 terms. The physical bounds on these polarization moments are set by the following inequalities:

$$\begin{array}{}\text{(31)}& \begin{array}{rl}\mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{20}}}(\mathrm{5}+\mathrm{6}\sqrt{\mathrm{5}}{\mathit{\rho }}_{\mathrm{10}}+\mathrm{10}{\mathit{\rho }}_{\mathrm{20}}+\mathrm{2}\sqrt{\mathrm{5}}{\mathit{\rho }}_{\mathrm{30}})\le \mathrm{1}\\ \mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{20}}}(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}{\mathit{\rho }}_{\mathrm{10}}-\mathrm{10}{\mathit{\rho }}_{\mathrm{20}}-\mathrm{6}\sqrt{\mathrm{5}}{\mathit{\rho }}_{\mathrm{30}})\le \mathrm{1}\\ \mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{20}}}(\mathrm{5}-\mathrm{2}\sqrt{\mathrm{5}}{\mathit{\rho }}_{\mathrm{10}}-\mathrm{10}{\mathit{\rho }}_{\mathrm{20}}+\mathrm{6}\sqrt{\mathrm{5}}{\mathit{\rho }}_{\mathrm{30}})\le \mathrm{1}\\ \mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{20}}}(\mathrm{5}-\mathrm{6}\sqrt{\mathrm{5}}{\mathit{\rho }}_{\mathrm{10}}+\mathrm{10}{\mathit{\rho }}_{\mathrm{20}}-\mathrm{2}\sqrt{\mathrm{5}}{\mathit{\rho }}_{\mathrm{30}})\le \mathrm{1}\\ & \text{for}I=\mathrm{3}/\mathrm{2}.\end{array}\end{array}$$

The physical bounds on the three polarization moments constrain the spin density operator to the interior of the regular tetrahedron shown in Fig. 2. The vertices of the tetrahedron are at coordinates $\mathit{\{}{\mathit{\rho }}_{\mathrm{10}},{\mathit{\rho }}_{\mathrm{20}},{\mathit{\rho }}_{\mathrm{30}}\mathit{\}}$ given by $\mathit{\{}\pm \mathrm{1}/\mathrm{2}\sqrt{\mathrm{5}},-\mathrm{1}/\mathrm{2},\mp \mathrm{3}/\mathrm{2}\sqrt{\mathrm{5}}\mathit{\}}$ and $\mathit{\{}\pm \mathrm{3}/\mathrm{2}\sqrt{\mathrm{5}},\mathrm{1}/\mathrm{2},\pm \mathrm{1}/\mathrm{2}\sqrt{\mathrm{5}}\mathit{\}}$. Each vertex corresponds to a pure-state density operator, in which only one state is populated. The z polarization is related to the rank-1 polarization moment ρ₁₀ through Eq. (18).

The tetrahedron in Fig. 2 corresponds to a regular simplex in three dimensions.

4.4 Higher spins

The treatment above is readily extended to higher spins. For isolated spins-I, the bounding figure is given by a regular simplex in 2I dimensions. For example, the four-dimensional bounding simplex of the polarization moments for spin I=2 is called a 5-cell or pentachoron (Coxeter, 1963); the five-dimensional bounding simplex of the polarization moments for spin $I=\mathrm{5}/\mathrm{2}$ is called a 5-simplex or hexateron (Coxeter, 1963), and so on. Regular high-dimensional polytopes have been exploited before in NMR, albeit in a different context (Pileio and Levitt, 2008; Mamone et al., 2010; Levitt, 2010).

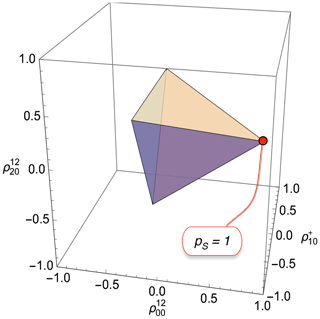
Figure 3 Physical bounds on the rank-0 polarization moment ${\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}}$, the rank-1 polarization moment ${\mathit{\rho }}_{\mathrm{10}}^{+}$, and the rank-2 polarization moment ${\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}}$ for spin-1/2 pairs. The shaded tetrahedron shows the physically accessible region. The vertices correspond to pure-state density operators for each of the four singlet or triplet states. The annotation shows the vertex for exclusive population of the singlet state (corresponding to pure parahydrogen in the case of H₂ gas).

4.5 Spin-1/2 pairs

For spin-1/2 pairs, the symmetric μ=0 subspace is of dimension 4, spanned by the four symmetric spherical tensor operators given in Eq. (19). Since the polarization moment ${\mathit{\rho }}_{\mathrm{00}}^{\mathrm{0}}$ is fixed (Eq. 20), the symmetric part of the spin density operator may be described as a point with coordinates $\mathit{\{}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}},{\mathit{\rho }}_{\mathrm{10}}^{+},{\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}}\mathit{\}}$, given by its projections onto the three orthonormal spherical tensor operators $\mathit{\{}{\mathbb{T}}_{\mathrm{00}}^{\mathrm{12}},{\mathbb{T}}_{\mathrm{10}}^{+},{\mathbb{T}}_{\mathrm{20}}^{\mathrm{12}}\mathit{\}}$. The density operator may also include components that are antisymmetric with respect to exchange: these components lie outside this three-dimensional subspace and are not considered further here.

The physical bounds on the symmetrical polarization moments $\mathit{\{}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}},{\mathit{\rho }}_{\mathrm{10}}^{+},{\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}}\mathit{\}}$ are set by the following inequalities:

$$\begin{array}{}\text{(32)}& \begin{array}{rl}\mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}})\le \mathrm{1}\\ \mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{12}}}(\mathrm{3}-\mathrm{2}\sqrt{\mathrm{3}}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}}+\mathrm{6}\sqrt{\mathrm{2}}{\mathit{\rho }}_{\mathrm{10}}^{+}+\mathrm{2}\sqrt{\mathrm{6}}{\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}})\le \mathrm{1}\\ \mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{12}}}(\mathrm{3}-\mathrm{2}\sqrt{\mathrm{3}}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}}-\mathrm{4}\sqrt{\mathrm{6}}{\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}})\le \mathrm{1}\\ \mathrm{0}\le & {\displaystyle \frac{\mathrm{1}}{\mathrm{12}}}(\mathrm{3}-\mathrm{2}\sqrt{\mathrm{3}}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}}-\mathrm{6}\sqrt{\mathrm{2}}{\mathit{\rho }}_{\mathrm{10}}^{+}+\mathrm{2}\sqrt{\mathrm{6}}{\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}})\le \mathrm{1}\\ & \text{for}\text{spin-1/2}\text{pairs}.\end{array}\end{array}$$

These inequalities constrain the polarization moments to the interior of the regular tetrahedron shown in Fig. 3. The vertices of the tetrahedron are at coordinates $\mathit{\{}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}},{\mathit{\rho }}_{\mathrm{10}}^{+},{\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}}\mathit{\}}$ given by

$$\begin{array}{}\text{(33)}& \mathit{\{}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}},{\mathit{\rho }}_{\mathrm{10}}^{+},{\mathit{\rho }}_{\mathrm{20}}^{\mathrm{12}}\mathit{\}}=\left\{\begin{array}{l}\mathit{\{}\frac{\mathrm{1}}{\mathrm{2}}{\mathrm{3}}^{\mathrm{1}/\mathrm{2}},\mathrm{0},\mathrm{0}\mathit{\}}\\ \mathit{\{}-\frac{\mathrm{1}}{\mathrm{2}}{\mathrm{3}}^{-\mathrm{1}/\mathrm{2}},{\mathrm{2}}^{-\mathrm{1}/\mathrm{2}},{\mathrm{6}}^{-\mathrm{1}/\mathrm{2}}\mathit{\}}\\ \mathit{\{}-\frac{\mathrm{1}}{\mathrm{2}}{\mathrm{3}}^{-\mathrm{1}/\mathrm{2}},-{\mathrm{2}}^{-\mathrm{1}/\mathrm{2}},{\mathrm{6}}^{-\mathrm{1}/\mathrm{2}}\mathit{\}}\\ \mathit{\{}-\frac{\mathrm{1}}{\mathrm{2}}{\mathrm{3}}^{-\mathrm{1}/\mathrm{2}},\mathrm{0},-(\mathrm{2}/\mathrm{3}{)}^{\mathrm{1}/\mathrm{2}}\mathit{\}}\end{array}\right.\end{array}$$

Each vertex corresponds to a pure-state density operator, in which the singlet state or one of the three triplet states is exclusively populated.

The highlighted point in Fig. 3 has coordinates $\mathit{\{}\frac{\mathrm{1}}{\mathrm{2}}{\mathrm{3}}^{\mathrm{1}/\mathrm{2}},\mathrm{0},\mathrm{0}\mathit{\}}$. From Eq. (21), this point corresponds to unit singlet polarization (p_S=1) and hence a pure singlet density operator:

$$\begin{array}{}\text{(34)}& \mathit{\rho }=\mathrm{|}{S}_{\mathrm{0}}\rangle \langle S_{\mathrm{0}}\mathrm{|},\end{array}$$

where the singlet state is given by (Levitt, 2019)

$$\begin{array}{}\text{(35)}& \mathrm{|}{S}_{\mathrm{0}}\rangle ={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}(\mathrm{|}\mathit{\alpha }\mathit{\beta }\rangle -\mathrm{|}\mathit{\beta }\mathit{\alpha }\rangle )\end{array}$$

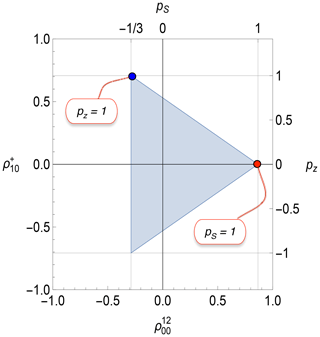
Figure 4 Physical bounds on the rank-0 polarization moment ${\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}}$ and the rank-1 polarization moment ${\mathit{\rho }}_{\mathrm{10}}^{+}$ for spin-1/2 pairs. The corresponding values of the z polarization p_z and singlet polarization p_S are also shown. The singlet polarization p_S (top horizontal axis) and rank-0 polarization moment ${\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}}$ (lower horizontal axis) are related through Eq. (21). The shaded triangle shows the physically accessible region. The annotations show the vertices for exclusive population of the singlet state (red) and for maximal z polarization (blue). Note that complete z polarization is accompanied by singlet polarization of $p_{\mathrm{S}}=-\mathrm{1}/\mathrm{3}$.

A projection of the tetrahedral bound in Fig. 3 onto the $\mathit{\{}{\mathit{\rho }}_{\mathrm{00}}^{\mathrm{12}},{\mathit{\rho }}_{\mathrm{10}}^{+}\mathit{\}}$ plane is shown in Fig. 4. The corresponding values of the singlet polarization p_S and z polarization p_z are shown on the axes, with the conversion factors given in Eqs. (21) and (22). The red point in Fig. 4 shows that maximal singlet polarization is necessarily accompanied by zero z polarization. In the case that the spin-1/2 pair is composed of the two proton nuclei of H₂, the red point corresponds to the spin density operator of pure parahydrogen (Farkas, 1935).

The blue point in Fig. 4 shows that maximal z polarization is necessarily accompanied by singlet polarization of $p_{\mathrm{S}}=-\mathrm{1}/\mathrm{3}$. This reflects the fact that maximal z polarization can only be achieved by depleting the singlet state at the expense of one of the triplet states. This fact may be exploited experimentally to generate hyperpolarized (negative) long-lived singlet order by the application of low-temperature dynamic nuclear polarization to spin-pair systems (Tayler et al., 2012; Bornet et al., 2014; Mammoli et al., 2015). Analogous phenomena are observed in more complex spin systems, such as methyl groups (Dumez et al., 2017) and deuterated moieties (Kress et al., 2019).

The physical bounds depicted in Figs. 3 and 4 are an intrinsic property of the spin-pair density operator and are completely independent of the spin Hamiltonian and its symmetry properties. Hence, these bounds apply to both magnetically equivalent and magnetically inequivalent spin-1/2 pairs. Nevertheless, since the spin Hamiltonian of magnetically inequivalent spin-1/2 pairs lacks exchange symmetry, it is also true that the density operator of magnetically inequivalent pairs readily accesses dimensions of Liouville space which are not exchange-symmetric and which are not included in these pictures. Hence, although Figs. 3 and 4 are equally valid for magnetically equivalent and inequivalent systems, there are additional dimensions which are not represented in these pictures and which are particularly relevant for the magnetically inequivalent case.

The geometry of the physical bounds is independent of the operator basis. Although a spherical tensor operator basis has been used in the discussion above, bounds of the same form are generated in any orthonormal operator basis, albeit with an overall rotation that depends on the relationship of the two bases. For example, if the ket–bra operator products |i〉〈j| are used as the basis of Liouville space, where $i,j\in \mathit{\left\{}\mathrm{1}\mathrm{\dots }{N}_H\mathit{\right\}}$, then the N_H vertices of the bounding simplex are located at coordinates $\mathit{\{}\mathrm{1},\mathrm{0},\mathrm{0}\mathrm{\dots }\mathit{\}}$, $\mathit{\{}\mathrm{0},\mathrm{1},\mathrm{0},\mathrm{0}\mathrm{\dots }\mathit{\}}$, $\mathit{\{}\mathrm{0},\mathrm{0},\mathrm{1},\mathrm{0},\mathrm{\dots }\mathit{\}}$, etc., representing the pure-state density operators with exclusive population of a single Hilbert-space state.

Figure 5 von Neumann entropy S_vN plotted against the rank-1 polarization moment ρ₁₀ and the z polarization p_z for isolated spins-1/2, for the case of zero transverse polarizations $p_x=p_y=\mathrm{0}$. The maximum value of S_vN is ln 2≃0.693.

5 von Neumann entropy

Quantum statistical mechanics uses the von Neumann entropy (vNE) to describe the disorder in, or absence of information about, a quantum system (Breuer and Petruccione, 2010; Rodin et al., 2020). It is derived from the spin density operator as follows:

$$\begin{array}{}\text{(36)}& S_{\mathrm{vN}}=-\text{Tr}\mathit{\left\{}\mathit{\rho }\ln \mathit{\rho }\mathit{\right\}}.\end{array}$$

The vNE for a system in a pure quantum state is zero, while the vNE for a system with equal populations of N_H quantum states, and no coherences, is given by S_vN=ln N_H.

5.1 Spins-1/2

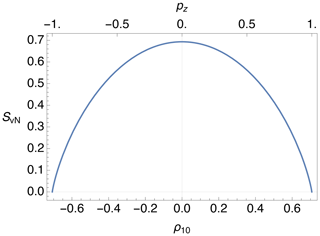
The von Neumann entropy S_vN is plotted against the rank-1 polarization moment ρ₁₀ in Fig. 5, assuming that ρ_1μ=0 for $\mathit{\mu }=\pm \mathrm{1}$. The corresponding value of the z polarization $p_z=\sqrt{\mathrm{2}}{\mathit{\rho }}_{\mathrm{10}}$ is shown on the top margin of the plot. The entropy goes to zero for complete z polarization in the positive or negative sense ($p_z=\pm \mathrm{1}$) and attains the maximum value of S_vN=ln 2 for zero polarization. The maximum entropy of ln 2 reflects the equal populations of the two Zeeman eigenstates and absence of coherences, for a completely saturated system.

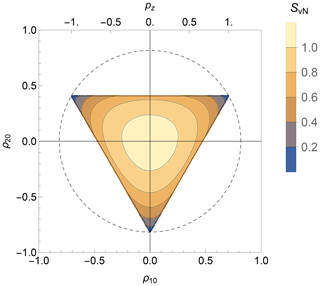
Figure 6 The von Neumann entropy S_vN is shown as a contour plot against the rank-1 and rank-2 polarization moments for isolated spins-1, for the case of ρ_λμ=0 for μ≠0. Only the physical region is shown (see Fig. 1). The corresponding value of the z polarization $p_z={\mathrm{2}}^{\mathrm{1}/\mathrm{2}}{\mathit{\rho }}_{\mathrm{10}}$ is shown along the top edge. The maximum value of the von Neumann entropy, reached at the origin, is ln 3≃1.10.

5.2 Spins-1

For isolated spins-1, the von Neumann entropy is a function of the rank-1 and rank-2 polarization moments, assuming that all polarization moments ρ_λμ vanish for μ≠0. Figure 6 shows a contour plot of the von Neumann entropy against ρ₁₀ and ρ₂₀, assuming that all polarization moments with μ≠0 vanish. Only the physically allowed region is shown, delineated by the triangle, as in Fig. 1. The entropy goes to zero at the three vertices, which correspond to the pure-state density operators with 100 % population of a single state. The von Neumann entropy reaches the maximum value of ln 3 at the centre of the plot, corresponding to ${\mathit{\rho }}_{\mathrm{10}}={\mathit{\rho }}_{\mathrm{20}}=\mathrm{0}$. The value of ln 3 reflects the equal distribution of population over the three spin states.

5.3 Higher spins

The behaviour of the von Neumann entropy is readily anticipated for higher spin quantum numbers. The entropy vanishes at the (2I+1) vertices of the 2I-simplex which bounds the physical region. The entropy maximum of ln (2I+1) is reached at the origin of the space, which corresponds to equal populations for all of the 2I+1 spin states.

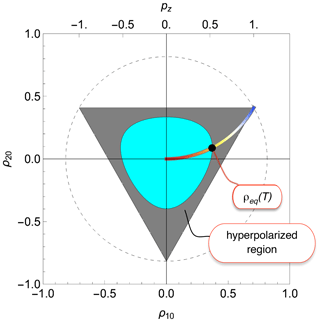
Figure 7 The coloured arc shows the set of thermal equilibrium density operators for spins-1 subjected to a dominant magnetic field. The spin temperature is indicated by colour, progressing from high (red) to low (blue). The black dot indicates the thermal equilibrium density operator at a particular temperature T. All points within the dark grey region represent hyperpolarized states of the spin-1 ensemble (density operators) at temperature T.

6 Hyperpolarization

6.1 Thermal equilibrium

Thermal equilibrium with the environment at temperature T is reached when the density operator adopts the following form:

$$\begin{array}{}\text{(37)}& {\mathit{\rho }}_{\mathrm{eq}}\left(T\right)={\displaystyle \frac{\exp \mathit{\{}-\textcolor{red}{}{H}_{\mathrm{coh}}/k_{B}T\mathit{\}}}{\text{Tr}\mathit{\left\{}\exp \mathit{\right\{}-\textcolor{red}{}{H}_{\mathrm{coh}}/k_{B}T\mathit{\left\}}\mathit{\right\}}}},\end{array}$$

where H_coh is the coherent part of the spin Hamiltonian (excluding all fluctuating terms which drive dissipation). Equation (37) describes a Boltzmann distribution of spin-state populations under the coherent Hamiltonian H_coh.

In many cases, the coherent Hamiltonian is dominated by the Zeeman interaction with the main magnetic field, H_coh≃ω⁰I_z, where the Larmor frequency is ${\mathit{\omega }}^{\mathrm{0}}=-\mathit{\gamma }{B}^{\mathrm{0}}$, and B⁰ is the magnetic field. In this case the thermal equilibrium density operator is given by

$$\begin{array}{}\text{(38)}& {\mathit{\rho }}_{\mathrm{eq}}\simeq {\displaystyle \frac{\exp \mathit{\left\{}\mathit{\beta }{I}_z\mathit{\right\}}}{\text{Tr}\mathit{\left\{}\exp \mathit{\right\{}\mathit{\beta }{I}_z\mathit{\left\}}\mathit{\right\}}}},\end{array}$$

where the normalized inverse temperature is $\mathit{\beta }=-\textcolor{red}{}{\mathit{\omega }}^{\mathrm{0}}/k_{B}T$. Since Eq. (38) is non-linear in I_z, the thermal equilibrium density operator contains high-rank polarization moments in thermal equilibrium.

The coloured arc in Fig. 7 shows the set of thermal equilibrium density operators for a dominant Zeeman interaction (Eq. 38), over a range of spin temperatures. Blue denotes a low spin temperature (β→∞), while red denotes a high spin temperature (β→0). Note the increase in the rank-2 polarization moment ρ₂₀ at low spin temperatures.

6.2 A criterion of hyperpolarization

The von Neumann entropy in thermal equilibrium at temperature T is given by

$$\begin{array}{}\text{(39)}& S_{\mathrm{vN}}^{\mathrm{eq}}\left(T\right)=-\text{Tr}\mathit{\left\{}{\mathit{\rho }}_{\mathrm{eq}}\right(T\left)\ln {\mathit{\rho }}_{\mathrm{eq}}\right(T\left)\mathit{\right\}},\end{array}$$

where the thermal equilibrium density operator is given by Eq. (37). We propose the following criterion of hyperpolarization:

$$\begin{array}{}\text{(40)}& S_{\mathrm{vN}}<S_{\mathrm{vN}}^{\mathrm{eq}}\left(T\right)\left(\text{criterion of hyperpolarization}\right),\end{array}$$

where T is the temperature of the environment. Note that this definition of hyperpolarization makes no explicit mention of population differences or the existence of a net magnetic moment in a certain direction.

The criterion in Eq. (40) identifies a region of Liouville space which is occupied by hyperpolarized states. For example, since the black dot in Fig. 7 indicates the thermal equilibrium density operator for spins I=1 at temperature T, the contour line $S_{\mathrm{vN}}=S_{\mathrm{vN}}^{\mathrm{eq}}\left(T\right)$ delineates the region of hyperpolarization at temperature T. All density operators which are inside the dark grey region represent physically realizable hyperpolarized states of the spin ensemble.

Being inside the dark grey region is a sufficient but not necessary criterion of hyperpolarization. Points outside the dark grey region but within the pale blue region might also represent hyperpolarized states, in the case that polarization moments which are not represented in the diagram, i.e. ρ_λμ with $\mathit{\{}\mathit{\lambda },\mathit{\mu }\mathit{\}}\ne \mathit{\{}\mathrm{1},\mathrm{0}\mathit{\}}$ and {2,0}, are sufficiently large.

The criterion in Eq. (40) is readily applied to higher spin systems, including coupled spin systems. Under this definition, parahydrogen is hyperpolarized, since the corresponding density operator has a von Neumann entropy of zero, which is lower than that of any thermal equilibrium state at finite temperature, even though pure parahydrogen possesses no magnetic moment or net angular momentum in a given direction.

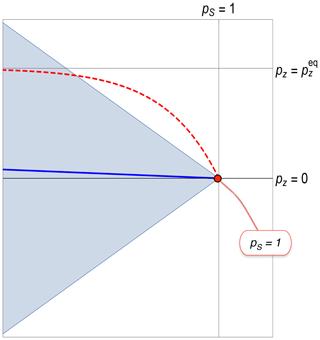
Figure 8 Non-equilibrium spin dynamics for an ensemble of spin-1/2 pairs, with T_S≫T₁, where T_S is the rate constant for the decay of singlet order, and T₁ is the rate constant for the equilibration of z polarization. The plot shows an expanded view of Fig. 4 in the vicinity of the red dot, which represents an initial state of 100 % singlet polarization. Dashed red line: trajectory predicted by the inhomogeneous master equation. Solid blue line: trajectory predicted by the Lindbladian master equation. Both trajectories eventually lead to the same thermal equilibrium state, represented by a point with coordinates $\mathit{\{}\mathrm{0},{p_z}^{\mathrm{eq}}\mathit{\}}$, which is well beyond the left-hand edge of the plotted region and is not shown.

7 Non-equilibrium spin dynamics

The dynamics of the spin density operator is governed by a differential equation called the master equation which takes into account coherent influences on the spin system (such as external magnetic fields and non-fluctuating components of the spin interactions) as well as relaxation effects. Various forms of the master equation have been proposed. The most widely used form is called the inhomogeneous master equation, which has the following form:

$$\begin{array}{}\text{(41)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathit{\rho }=-i{\widehat{H}}_{\mathrm{coh}}\mathit{\rho }\left(t\right)+\widehat{\mathrm{\Gamma }}\left(\mathit{\rho }\right(t)-{\mathit{\rho }}_{\mathrm{eq}}),\end{array}$$

where ${\widehat{H}}_{\mathrm{coh}}$ is the commutation superoperator of the coherent Hamiltonian, and $\widehat{\mathrm{\Gamma }}$ is the relaxation superoperator (Redfield, 1965; Abragam, 1961; Ernst et al., 1987). The equilibrium spin density operator ρ_eq is given by Eq. (37).

The inhomogeneous master Eq. (41) is valid for high-entropy states which are close to equilibrium and is a standard component of NMR theory (Redfield, 1965; Abragam, 1961; Ernst et al., 1987). However, in a previous paper (Bengs and Levitt, 2020), we showed that Eq. (41) loses validity for low-entropy states and may, in some cases, lead to non-physical predictions. We proposed a Lindbladian master equation, which has a wider range of validity.

This point is reinforced by Fig. 8, which compares the predictions of the inhomogeneous and Lindbladian master equations when applied to spin-1/2 pairs in a low-entropy state of pure singlet polarization. The initial state of pure singlet order is shown by the red dot. The plot shows an expanded view of Liouville space, in the vicinity of the initial condition. The physical bounds of Liouville space are indicated by the blue triangle, as in Fig. 4.

The red dashed line shows the trajectory predicted by the IME, in the case that T_S≫T₁, where T_S is the relaxation time constant for singlet order (Levitt, 2019) and T₁ is the relaxation time constant for z polarization. Since T₁ is relatively short, the z polarization rapidly assumes its thermal equilibrium value ${\mathit{\rho }}_z^{\mathrm{eq}}$, which is finite in the presence of a strong magnetic field. However, as shown in Fig. 8, this leads the density operator into a forbidden region outside the physical boundary of Liouville space. This proves that the inhomogeneous master equation must be invalid in this regime.

The predicted trajectory of the Lindbladian master equation, as described in Bengs and Levitt (2020), is shown by the blue line. This uneventful trajectory always stays well within the physical boundary of Liouville space.

8 Conclusions

This article has been an exploration of the geometry and physical boundary of Liouville space, the home territory of all spin density operators. In the past, most NMR experiments have only explored a tiny region of this space, very close to the origin (except for the fixed projection onto the unity operator). However, NMR experiments are increasingly performed on highly non-equilibrium spin states, which are sometimes located on or near the physical Liouville space boundary. We hope that this article is useful as a partial guide for wanderers in this region.

The word “partial” is used deliberately. So far, we have concentrated on the aspects of Liouville space which concern populations, and in the case of spin-1/2 pairs, on operators that are exchange-symmetric. The map still needs to be completed by delineating the physical bounds on coherences and on operators for multiple-spin systems, including those that are not exchange-symmetric. There has already been significant progress in that direction (Goyal et al., 2016; Szymański et al., 2018).

The physical bounds discussed in this article should not be confused with the bounds on the unitary transformations of density operators (Sørensen, 1990; Levitt, 1992a, b; Nielsen and Sørensen, 1995; Levitt, 2016), which may also be represented by convex polytopes (Levitt, 1992a, b; Rodin et al., 2020). The relationship between these different geometric bounds is another topic for future research.