the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Improved NMR transfer of magnetization from protons to half-integer spin quadrupolar nuclei at moderate and high magic-angle spinning frequencies
Jennifer S. Gómez
Andrew G. M. Rankin
Julien Trébosc
Frédérique Pourpoint
Yu Tsutsumi
Hiroki Nagashima
Olivier Lafon
Jean-Paul Amoureux
Half-integer spin quadrupolar nuclei are the only magnetic isotopes for the majority of the chemical elements. Therefore, the transfer of polarization from protons to these isotopes under magic-angle spinning (MAS) can provide precious insights into the interatomic proximities in hydrogen-containing solids, including organic, hybrid, nanostructured and biological solids. This transfer has recently been combined with dynamic nuclear polarization (DNP) in order to enhance the NMR signal of half-integer quadrupolar isotopes. However, the cross-polarization transfer lacks robustness in the case of quadrupolar nuclei, and we have recently introduced as an alternative technique a D-RINEPT (through-space refocused insensitive nuclei enhancement by polarization transfer) scheme combining a heteronuclear dipolar recoupling built from adiabatic pulses and a continuous-wave decoupling. This technique has been demonstrated at 9.4 T with moderate MAS frequencies, νR≈10–15 kHz, in order to transfer the DNP-enhanced 1H polarization to quadrupolar nuclei. Nevertheless, polarization transfers from protons to quadrupolar nuclei are also required at higher MAS frequencies in order to improve the 1H resolution. We investigate here how this transfer can be achieved at νR≈20 and 60 kHz. We demonstrate that the D-RINEPT sequence using adiabatic pulses still produces efficient and robust transfers but requires large radio-frequency (rf) fields, which may not be compatible with the specifications of most MAS probes. As an alternative, we introduce robust and efficient variants of the D-RINEPT and PRESTO (phase-shifted recoupling effects a smooth transfer of order) sequences using symmetry-based recoupling schemes built from single and composite π pulses. Their performances are compared using the average Hamiltonian theory and experiments at B0=18.8 T on γ-alumina and isopropylamine-templated microporous aluminophosphate (AlPO4-14), featuring low and significant 1H–1H dipolar interactions, respectively. These experiments demonstrate that the 1H magnetization can be efficiently transferred to 27Al nuclei using D-RINEPT with (270090180) recoupling and using PRESTO with (1800) or (270090180) schemes at νR=20 or 62.5 kHz, respectively. The D-RINEPT and PRESTO recoupling schemes complement each other since the latter is affected by dipolar truncation, whereas the former is not.
We also analyze the losses during these recoupling schemes, and we show how these magnetization transfers can be used at νR=62.5 kHz to acquire in 72 min 2D HETCOR (heteronuclear correlation) spectra between 1H and quadrupolar nuclei, with a non-uniform sampling (NUS).
- Article
(4528 KB) - Full-text XML
-
Supplement
(1108 KB) - BibTeX
- EndNote
Quadrupolar nuclei with a nuclear spin quantum number , , or are the only NMR-active isotopes for over 60 % of the chemical elements of the first six periods of the periodic table, including six of the eight most abundant elements by mass in the Earth's crust: O, Al, Ca, Na, Mg and K (Ashbrook and Sneddon, 2014). A wide range of materials, including organic compounds, biological macromolecules, and nanostructured or hybrid materials, contain half-integer spin quadrupolar nuclei and protons. Proximities between these isotopes have notably been probed in solid-state NMR experiments by transferring the polarization of protons to half-integer quadrupolar nuclei through dipolar couplings under magic-angle spinning (MAS) conditions (Rocha et al., 1991; Hwang et al., 2004; Peng et al., 2007; Vogt et al., 2013; Chen et al., 2019). More recently, this polarization transfer has been combined under MAS with dynamic nuclear polarization (DNP) in order to enhance the NMR signals of half-integer spin quadrupolar nuclei (Vitzthum et al., 2012; Perras et al., 2015a; Nagashima et al., 2020). This approach has notably allowed for the detection of insensitive quadrupolar nuclei with low natural abundance, such as 17O or 43Ca, or low gyromagnetic ratio, γ, such as 47,49Ti, 67Zn or 95Mo, near surfaces of materials (Perras et al., 2015a, 2016, 2017; Blanc et al., 2013; Hope et al., 2017; Lee et al., 2017; Nagashima et al., 2020, 2021; Li et al., 2018).
This transfer has originally been achieved using cross-polarization under MAS (CPMAS) (Harris and Nesbitt, 1988). Nevertheless, this technique lacks robustness for quadrupolar nuclei since the spin-locking of the central transition (CT) between energy levels is sensitive to the strength of the quadrupole interaction, the offset, the chemical shift anisotropy (CSA) and the radio-frequency (rf) field inhomogeneity (Vega, 1992; Amoureux and Pruski, 2002; Tricot et al., 2011). Furthermore, CPMAS experiments require a careful adjustment of the rf field applied to the quadrupolar isotope in order to fulfill the Hartmann–Hahn conditions, , where ν1S and ν1H denote the amplitudes of the rf fields applied to the S quadrupolar isotope and to the protons, respectively; , , or ±2; and νR denotes the MAS frequency, while avoiding the rotary resonance recoupling (R3) with p=0, 1, 2 and 3 (Amoureux and Pruski, 2002; Ashbrook and Wimperis, 2009). Moreover, the magnetization of the quadrupolar nuclei cannot be spin-locked for some crystallite orientations, which leads to line-shape distortions (Barrie, 1993; Hayashi and Hayamizu, 1993; Ding and Mcdowell, 1995).
These issues have been circumvented by use of the PRESTO (phase-shifted recoupling effects a smooth transfer of order) scheme (Perras et al., 2015a, b; Zhao et al., 2004) and, more recently, the through-space refocused INEPT (denoted RINEPT hereafter) (Nagashima et al., 2020; Giovine et al., 2019). These schemes benefit from higher robustness than CPMAS since they do not employ a spin-lock on the quadrupolar channel but instead a limited number (two or three) of CT selective pulses. In these sequences, the dipolar interactions between protons and quadrupolar nucleus are reintroduced by applying on the 1H channel symmetry-based recoupling sequences, such as for PRESTO or for RINEPT (Zhao et al., 2001; Brinkmann and Kentgens, 2006a). In the case of recoupling sequences built from single square π pulses, the RINEPT sequence using (denoted RINEPT-) is more efficient than PRESTO at νR≥60 kHz because of its higher robustness to rf field inhomogeneity and 1H offset and CSA. At νR<20 kHz, the PRESTO technique is more efficient since the efficiency of RINEPT- is reduced by the increased losses due to 1H–1H interactions during the recoupling and the windows used to rotor synchronize the blocks, whereas the PRESTO sequence is devoid of these windows (Giovine et al., 2019).
Recently, we have introduced a novel variant of the RINEPT sequence by employing the recoupling built (i) from tanh/tan (tt) adiabatic inversion pulses, (ii) continuous-wave (CW) irradiations during the windows, and (iii) composite and π pulses on the 1H channel, in order to limit the losses due to 1H–1H interactions and improve the transfer efficiency at moderate MAS frequencies (Nagashima et al., 2020, 2021). This novel RINEPT variant, denoted RINEPT-CWc-, is more efficient than PRESTO and CPMAS at νR≈12.5 kHz, and it has been combined with DNP to detect the NMR signals of quadrupolar nuclei with small dipolar coupling with protons, including the low-γ isotopes, such as 47,49Ti, 67Zn or 95Mo, and unprotonated 17O nuclei. Furthermore, for quadrupolar nuclei subject to large dipolar interactions, such as 17O nuclei of OH groups, we have shown that a RINEPT-CWc- version with only two pulses on the quadrupolar channel is more efficient that its PRESTO counterpart (Nagashima et al., 2021).
However, several NMR experiments require the transfer of 1H magnetization to quadrupolar nuclei at νR>12.5 kHz. In particular, MAS frequencies of νR≥20 kHz are needed to avoid the overlap between the center bands and the spinning sidebands of satellite transitions (STs) in 27Al NMR spectra at 18.8 T. In addition, magnetization transfers at νR≥60 kHz are advantageous to acquire through-space heteronuclear correlation (D-HETCOR) 2D spectra between protons and quadrupolar nuclei endowed with high resolution along the 1H dimension since fast MAS averages out the 1H–1H dipolar couplings.
Concurrently, we have demonstrated that the efficiency of PRESTO transfers using the recoupling can be improved at νR=62.5 kHz using (270090180) composite π pulses as a basic inversion element, where the standard notation for the pulses is used: ξϕ denotes a rectangular, resonant rf pulse with flip angle ξ and phase ϕ in degrees (Giovine et al., 2019). More recently, and recoupling schemes built from (90−45904590−45) composite π pulses have been proposed, but they have not yet been incorporated into RINEPT transfers (Perras et al., 2019). Globally, no systematic study of the recouplings built from composite π pulses has been carried out.
In the present article, we investigate the use of RINEPT-CWc using an adiabatic recoupling scheme at the higher MAS frequencies of νR=20 and 62.5 kHz. We demonstrate using numerical simulations of spin dynamics and experiments on γ-alumina and isopropylamine-templated microporous aluminophosphate (AlPO4-14) (hereafter AlPO4-14) that the rf requirement of this technique increases with the 1H–1H dipolar interactions. In practice, this rf requirement is not compatible with the specifications of most MAS probes at νR≥20 kHz, even for moderate 1H–1H dipolar interactions. As an alternative, we introduce variants of the PRESTO and RINEPT sequences by selecting with average Hamiltonian (AH) theory recoupling schemes built from single rectangular or composite π pulses. Finally, using experiments on γ-alumina and AlPO4-14, which feature small and moderate 1H–1H dipolar interactions, respectively, we identify the most robust and efficient PRESTO and RINEPT transfers at B0=18.8 T with νR=20 and 62.5 kHz.
2.1 PRESTO
2.1.1 Single-quantum heteronuclear dipolar recoupling
A sequence, where N is an even positive integer and n and ν are integers, consists of pairs of elements , with radians an overall phase shift. ℛϕ is an inversion pulse with a duration of , where is the rotor period, and is an inversion pulse derived from ℛ by changing the sign of all phases. ℛ and ℛ′ are identical when they are amplitude modulated; i.e., all phase shifts are multiples of π. The rf field requirement of is equal to
where is the sum of the flip angles of the P individual pulses of the ℛ element.
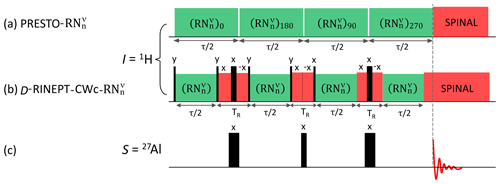
Figure 1The 1H → 27Al (a, c) PRESTO- and (b, c) D-RINEPT-CWc- pulse sequences. Those applied to the 1H channel are displayed in panels (a) and (b), whereas that applied to the 27Al channel is shown in panel (c). The narrow and broad black bars represent and π pulses, respectively. The acquisition of the free-induction decays (FIDs) (indicated with the vertical dashed line) starts after (a) the end of the block in the case of PRESTO or (b) on top of the echo shifted with with respect to the end of the last recoupling block in the case of RINEPT.
In the PRESTO sequence (Fig. 1a), symmetry-based γ-encoded schemes applied to the 1H channel reintroduce the |m|=2 space components and the single-quantum (SQ) terms of the heteronuclear dipolar couplings between the protons and the quadrupolar nuclei, as well as the 1H CSA, while they suppress the contributions of 1H isotropic chemical shifts, the heteronuclear J couplings with protons, and the 1H–1H dipolar couplings to the first-order AH (Zhao et al., 2004). The heteronuclear dipolar interaction is characterized by a space rank l and a spin rank λ. A γ-encoded |m|=2 SQ heteronuclear dipolar recoupling must selectively reintroduce the two components and of the heteronuclear dipolar coupling and 1H CSA with , while all other components must be suppressed.
During these recoupling schemes, the contribution of the dipolar coupling between I=1H and S nuclei to the first-order Hamiltonian is equal to (Zhao et al., 2004)
where symbols represent the shift operators, and the magnitude and phase of the recoupled I–S dipolar coupling are given by
and
respectively, where bIS is the dipolar coupling constant in rad/s, and κ is the scaling factor of the recoupled heteronuclear dipolar interaction, which depends on the symmetry and the ℛ element. The Euler angles relate the I–S vector to the MAS rotor frame, and t0 refers to the starting time of the recoupling. The norm of does not depend on the angle, since these recoupling schemes are γ encoded (Pileio et al., 2007; Martineau et al., 2012). The Hamiltonian of Eq. (2) does not commute among different spin pairs; hence, the PRESTO sequence is affected by dipolar truncation; i.e., the transfer to distant nuclei is attenuated by the stronger couplings with nearby spins (Bayro et al., 2009).
As mentioned above, the SQ heteronuclear dipolar recoupling schemes also reintroduce the 1H CSA with the same scaling factor κ but without commuting with the recoupled 1H–S dipolar interactions. Therefore, in the case of large 1H CSA, for instance at high magnetic fields, this interaction can interfere with the 1H–S dipolar couplings, especially with the small ones. These interferences can be limited by the use of the PRESTO-III variant, depicted in Fig. 1a, c (Zhao et al., 2004), in which three CT-selective pulses are applied to the S channel. Indeed, the CT-selective π pulses partly refocus the 1H CSA, which limits these interferences.
2.1.2 Selection of the recoupling sequence
On the basis of the AH and spin dynamics simulations, the and schemes built from single rectangular π pulses were selected for heteronuclear dipolar recoupling at moderate MAS frequencies, νR ≈10 kHz (Zhao et al., 2001), while, more recently, sequences based on symmetries , , , , , , and using (270090180) as inversion element were chosen for the measurement of 1H CSA at fast MAS frequencies, νR≈60–70 kHz (Pandey et al., 2015). We also transferred the proton polarization to 27Al nuclei at νR=62.5 kHz using PRESTO with recoupling built from a single rectangular π pulse (Giovine et al., 2019).
We screened here the schemes built from single rectangular and composite π pulses to achieve γ-encoded |m|=2 heteronuclear SQ dipolar recoupling at νR=20 or 62.5 kHz. Dipolar recoupling at νR≥60 kHz is useful to correlate the signals of quadrupolar nuclei with high-resolution 1H spectra without using homonuclear dipolar decoupling. We tested the three following composite π pulses: (1) (270090180), which is offset compensated and amplitude modulated and has been employed in several sequences (Giovine et al., 2019; Carravetta et al., 2000; Levitt, 2002; Pandey et al., 2015); (2) (90024090900), which compensates both rf inhomogeneity and offset (Freeman et al., 1980; Duong et al., 2019); and (3) (90−45904590−45), which has homonuclear decoupling properties (Madhu et al., 2001). Adiabatic pulses cannot be employed for SQ heteronuclear dipolar recoupling since they yield vanishing scaling factors for the rotational components with μ≠0 (Nagashima et al., 2018).
A total of 109 symmetries with , and were found which recouple the or rotational components of the 1H–S dipolar coupling and 1H CSA. We selected the recouplings based on those symmetries with rf field limited to ν1≤120 and 190 kHz for νR=20 and 62.5 kHz, respectively. We only considered the symmetries with ∘ since sequences with ϕ close to 90∘ are better compensated for rf field errors and inhomogeneities (Brinkmann and Kentgens, 2006b). The scaling factor, κ, of the recoupled 1H–S dipolar interaction was calculated using the “C and R symmetries” Mathematica package (Carravetta et al., 2000; Brinkmann and Levitt, 2001; Brinkmann et al., 2000; Brinkmann and Edén, 2004).
These symmetries eliminate the contribution of 1H–1H dipolar interactions to the first-order Hamiltonian but not their contribution to the second order. The cross terms between 1H–1H interactions in the second-order Hamiltonian can be written (Brinkmann and Edén, 2004):
where the sum is taken over all second-order cross terms {1,2} between the and rotational components of DD1 and DD2 1H–1H dipolar interactions, respectively. is the scaling factor of this cross term; and denote the component mi of the lith rank spatial irreducible spherical tensor in the MAS rotor-fixed frame and the component μi of the λith rank spin irreducible spherical tensor operator . Equation (5) indicates that the amplitude of the second-order Hamiltonian decreases at higher MAS frequencies. The magnitude of the cross terms between 1H–1H interactions was estimated by calculating the Euclidean norm (Hu et al., 2009; Gansmüller et al., 2013):
For each basic element ℛ, we selected the schemes with the highest ratio in order to minimize the interference of 1H–1H dipolar interactions with the 1H–S dipolar recoupling. Besides 1H–1H dipolar interactions, other cross terms involving 1H CSA and offset can also interfere with the 1H–S dipolar recoupling. These cross terms can be expressed by Eq. (5), in which DD1 and DD2 indexes are substituted by other interactions, such as 1H CSA or isotropic chemical shift (δiso). For the selected symmetries, we estimated the magnitude of the cross terms between 1H CSA or offset by calculating the Euclidean norms and given by Eq. (6).
The corresponding selected sequences are listed in Tables S1 and S2 in the Supplement for νR=20 and 62.5 kHz, respectively.
For νR=20 kHz, according to the AH, the sequence with the highest robustness to 1H–1H dipolar interactions is ). However, this recoupling is slightly less robust to 1H CSA and offset than ), which has already been reported. For this MAS frequency, the schemes using the chosen composite pulses either required rf fields greater than 120 kHz, e.g., ν1=130 and 173 kHz for the R26 schemes built from (90−45904590−45) and (270090180) pulses, or did not suppress efficiently the second-order cross terms between 1H–1H interactions because of small rf field (ν1≤62.5 kHz).
For νR=62.5 kHz, the sequences using composite π pulses recouple the 1H–S dipolar interaction with a higher scaling factor than those built from single π pulses. According to AH, the (90024090900) basic element leads to the highest robustness to 1H–1H interferences. Even if the amplitude of the cross terms is inversely proportional to the MAS frequency (Eq. 5), the amplitude of these terms is lower at νR=20 than 62.5 kHz. The (270090180) element is less robust to 1H–1H interferences but benefits from a high robustness to offset. The selected symmetries for this element include and , which have already been employed for the measurement of 1H CSA and the transfer of 1H polarization to half-integer quadrupolar nuclei at νR≥60 kHz (Giovine et al., 2019; Pandey et al., 2015). The scaling factors κ of the 1H–S dipolar interaction of the schemes built from single π pulses are small with ∘; hence, we also selected in Table S3 those with an extended ϕ range of 20–160∘. These recoupling schemes are less robust to offset than the schemes built from (270090180) element.
2.2 D-RINEPT
2.2.1 Zero-quantum heteronuclear dipolar recoupling
In the D-RINEPT sequence, the 1H–S dipolar interactions are reintroduced under MAS by applying non-γ-encoded two-spin order dipolar recoupling to the 1H channel. These schemes reintroduce the |m|=2 space components and the zero-quantum (0Q) terms of the 1H–S dipolar interaction and 1H CSA; i.e., the rotational components , while they suppress the contributions of 1H isotropic chemical shifts, the heteronuclear J couplings with protons, and the 1H–1H dipolar couplings to the first-order AH (Brinkmann and Kentgens, 2006a, b). The contribution of the 1H–S dipolar coupling to this Hamiltonian is equal to (Giovine et al., 2019; Brinkmann and Kentgens, 2006a; Lu et al., 2012)
where
The norm of depends on the φ phase, given by Eq. (4), and hence on the angle. Therefore, these two-spin order dipolar recoupling schemes are non-γ-encoded. The Hamiltonian of Eq. (7) commutes among different spin pairs; hence, these recoupling schemes are not affected by dipolar truncation. Similarly, the recoupled 1H CSA contribution to the first-order Hamiltonian is proportional to Iz and hence also commutes with the recoupled 1H–S dipolar interactions and does not interfere with the heteronuclear dipolar recoupling.
2.2.2 Selection of the recoupling sequence
Different sequences have been proposed to achieve non-γ-encoded |m|=2 two-spin order dipolar recoupling, including (i) symmetries , , , , and for n=3, 4, 5, 6, 7 and 8 using single π pulses as basic element, which have been employed to measure 1H–17O dipolar couplings at νR=50 kHz (Brinkmann and Kentgens, 2006b); (ii) recoupling built from a single π pulse, which corresponds to the sequence and has been employed in the RINEPT scheme (Nagashima et al., 2021; Giovine et al., 2019); (iii) and schemes using a (90−45904590−45) composite π pulse as a basic element, which have been incorporated into D-HMQC (heteronuclear multiple quantum coherence) at νR=36 kHz (Perras et al., 2019), and (iv) schemes built from a (tt) adiabatic pulse, which have been used in the RINEPT sequence (Nagashima et al., 2021, 2020). During the (tt) pulse, the instantaneous rf amplitude is equal to
where is the peak amplitude of the rf field, t refers to the time since the start of the pulse, which lasts when incorporated into the recoupling scheme. The parameter ξ determines the rise and fall times of the pulse. Hence, in the frequency-modulated (FM) frame (Garwood and DelaBarre, 2001), the frequency offset is
where is the peak amplitude of the carrier frequency modulation, and θ determines the frequency sweep rate in the center of the pulse. Here, we employed ξ=10 and (Kervern et al., 2007; Nagashima et al., 2018, 2020).
We screened here the schemes built from (1800), (270090180), (90024090900) and (90−45904590−45) inversion elements. A total of 58 symmetries with , and were found which recouple the rotational components of the 1H–S dipolar coupling and 1H CSA. We only considered the symmetries with ∘ since the currently employed non-γ-encoded |m|=2 two-spin order heteronuclear dipolar recoupling schemes have ∘.
We calculated the scaling factor of the recoupled 1H–S dipolar interaction and the Euclidean norm of the cross terms between 1H–1H interactions using the “C and R symmetries” Mathematica package. For each basic element ℛ, we selected the schemes with the highest ratios . The selected sequences are listed in Table S4, along with the parameters of the schemes built from the different basic elements ℛ for the sake comparison. For these sequences, we calculated the Euclidean norms, and , in order to estimate the magnitudes of the cross terms between 1H CSA and offset.
According to the AH, the (90024090900) composite π pulse yields the highest robustness to 1H–1H dipolar interactions. However, the rf field requirement of the sequences built from this composite pulse, , is not compatible at νR=62.5 kHz with most 1.3 mm MAS probes (e.g., ν1=291 kHz for ). Furthermore, the highest robustness to 1H CSA and offset are achieved using the (270090180) composite π pulse. The schemes benefit from the highest robustness to 1H CSA because of the three-step multiple-quantum super-cycle (Brinkmann and Edén, 2004; Brinkmann and Kentgens, 2006a). Contrary to the with |m|=2 SQ heteronuclear dipolar recouplings, the rf field of the with |m|=2 two-spin order schemes is always higher than 2νR since these symmetries with 2n>N, such as , have smaller κ scaling factors for the basic elements employed here.
In the case of the adiabatic (tt) sequences, the determination of the scaling factors of the first- and second-order terms of the effective Hamiltonian is more cumbersome since they depend on the , , ξ and θ parameters (Nagashima et al., 2018). For example, the scaling factor of the and schemes is κ=0.31 for , ξ=10 and θ=87∘, and this value monotonously decreases for increasing ratios.
2.2.3 D-RINEPT-CWc sequence
The D-RINEPT-CWc sequence is displayed in Fig. 1b and c. The 1H–S dipolar couplings are reintroduced by applying the schemes listed in Table S4 during the defocusing and refocusing delays τ, which are identical in this article, even if distinct delays can improve the transfer efficiency (Nagashima et al., 2021). As the two-spin order recoupling schemes are non-γ-encoded, they must be rotor synchronized. We used here a delay of TR between two successive blocks. In the D-RINEPT-CWc sequence, a CW irradiation is applied during these delays in order to limit the losses due to 1H–1H dipolar interactions (Nagashima et al., 2021). The nutation during this CW irradiation is eliminated by employing CW irradiations with opposite phases. Furthermore, the robustness to 1H rf field inhomogeneity is improved by replacing the first π and second pulses by composite (90018090900) and (9090900) pulses, respectively, with the CW irradiation being applied between the individual pulses (Freeman et al., 1980; Levitt and Freeman, 1979).
3.1 Simulation parameters
All simulations were performed using version 4.1.1 of the SIMPSON package (Bak et al., 2000). The powder average was performed using 462 Euler angles relating the molecular and rotor frames. This set of angles was obtained by considering 66 {αMR,βMR} pairs and 7 γMR angles. The {αMR,βMR} values were selected according to the REPULSION algorithm (Bak and Nielsen, 1997), while the γMR angles were regularly stepped from 0 to 360∘.
To accelerate the simulations, we used a 1H → 15N RINEPT transfer instead of the 1H → 27Al one, because the computing time is proportional to the cube of the size of the density matrix. Furthermore, in RINEPT experiments, only CT-selective pulses are applied to the quadrupolar nuclei; hence, the contribution of the STs to the signal can be disregarded. The 1H → 15N RINEPT transfer was simulated for a 15N1H4 spin system. A similar approach has already been applied for the simulation of the RINEPT transfer from protons to quadrupolar nuclei (Nagashima et al., 2021; Giovine et al., 2019). This 15N1H4 spin system comprises a tetrahedron of four protons with a 15N nucleus on one of its symmetry axes. The dipolar coupling constants between protons are all equal to , 7 or 15 kHz. The dipolar coupling between the 15N nucleus and its closest 1H neighbor is Hz, corresponding to a 1H–27Al distance of 2.3 Å, typical of the distance between the protons of hydroxyl groups and the Al atoms of the first surface layer of hydrated γ-alumina (Lee et al., 2014). All protons were subject to a CSA of 6 kHz, i.e., 7.5 ppm at 18.8 T, with a null asymmetry parameter (Liang et al., 2018). We simulated the 1H → 15N RINEPT-CWc sequences by incorporating either (tt) or (tt) recoupling schemes. We used a static magnetic field of 18.8 T, for which the 1H and 15N Larmor frequencies were equal to 800 and 81 MHz, respectively, and MAS frequencies of νR=20 or 62.5 kHz. The defocusing and refocusing periods were both equal to their optimal values τ=650 or 640 µs at νR=20 or 62.5 kHz, respectively. The rf field nutation frequency on the 1H channel was equal to 200 kHz during the and π pulses that do not belong to the recoupling sequence, as well as the CW irradiation, whereas the pulses applied to S =15N nuclei were considered ideal Dirac pulses. For the (tt) adiabatic pulses, the simulations were performed with and ratios ranging from 0.5 to 10 and from 10 to 200, respectively. All other pulses were applied on resonance. The density matrix before the first pulse was equal to . We normalized the transfer efficiency of the 1H → 15N RINEPT sequences to the maximal signal for a 1H → 15N through-bond RINEPT sequence made of ideal Dirac pulses in the case of a 15N–1H spin system with a J-coupling constant of 150 Hz.
3.2 Optimal adiabatic recoupling
The transfer efficiency of RINEPT using schemes built from adiabatic (tt) pulses depends on and parameters. For a similar 15N1H4 spin system with and kHz, spinning at νR=12.5 kHz, we showed using numerical simulations that a maximal transfer efficiency was achieved provided that and (Nagashima et al., 2021). In practice, we used kHz and MHz.
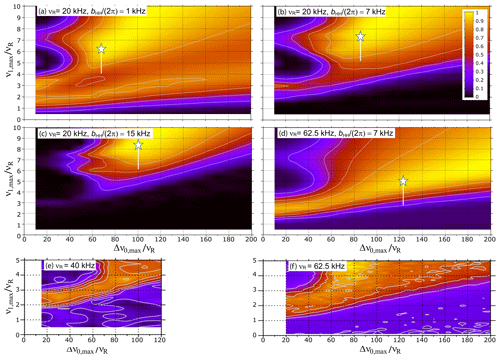
Figure 2(a–d) Simulated transfer efficiency of 1H → 15N D-RINEPT- sequence for a 15N1H4 spin system as a function of and for νR=20 and 62.5 kHz and = (a) 1 kHz, (b, d) 7 kHz and (c) 15 kHz. (e, f) Experimental 1H → 15N D-RINEPT- signal of L-histidine ⋅ HCl as a function of and at 18.8 T with νR = (e) 40 kHz or (f) 62.5 kHz. In panels (a)–(d) the white star indicates recoupling conditions with minimal rf field leading to maximal transfer efficiency, and the white vertical line mimics the rf field distribution within the coil.
Similar simulations were performed here for νR=20 or 62.5 kHz. As seen in Fig. 2a–c, at a given MAS frequency, higher 1H–1H dipolar couplings require higher rf field and broader carrier frequency sweep so that the (tt) pulses remain adiabatic in spite of the modulation of the 1H–1H dipolar couplings by MAS (Nagashima et al., 2021; Kervern et al., 2007). For kHz, the minimal ratio decreases for higher MAS frequencies (compare Fig. 2b and d) since the contribution of the modulation of 1H–1H dipolar couplings by MAS to the first adiabaticity factor is proportional to (; hence, values proportional to , i.e., ratio inversely proportional to , are sufficient to maintain the adiabaticity of the pulses (Kervern et al., 2007). Nevertheless, Fig. 2d indicates that the (tt) recoupling requires kHz for νR=62.5 kHz, which is hardly compatible with the specifications of most 1.3 mm MAS probes. Similar transfer efficiencies were simulated for the RINEPT sequence with (tt) recoupling scheme (not shown).
4.1 Samples and experimental conditions
L-[U-15N]-histidine ⋅ HCl (hereafter referred to as “histidine”) and isotopically unmodified γ-alumina were purchased from Merck, and AlPO4-14 was prepared as described previously (Antonijevic et al., 2006).
All 1H → S RINEPT-CWc and PRESTO-III experiments were performed at B0=18.8 T on Bruker BioSpin Avance NEO spectrometers equipped with double-resonance 1H/X probes.
1H → 15N RINEPT-CWc-(tt) experiments on histidine were performed with 1.3 and 0.7 mm MAS probes spinning at νR=40 or 62.5 kHz, with defocusing and refocusing delays equal to τ = 375 and 384 µs, respectively. The rf field of the 1H and π pulses, which do not belong to the recoupling scheme, was equal to 200 kHz, that of the continuous-wave irradiation to 100 kHz, and that of the 15N pulses to 62 kHz. 1H decoupling with an rf field of 16 kHz was applied during the acquisition. The pulses on the 1H channel were applied on resonance, whereas those on the 15N channel were applied at the isotropic chemical shift of the 15NHτ signal (172 ppm). These 1D spectra resulted from averaging eight transients with a relaxation delay of 3 s. The 15N isotropic chemical shifts were referenced to an aqueous saturated solution of NH4NO3 using [15N]-glycine as a secondary reference.
Table 1Comparison of the performances of 1H → 27Al RINEPT-CWc and PRESTO transfers using various recouplings for AlO6 signal of γ-alumina at νR=20 kHz.
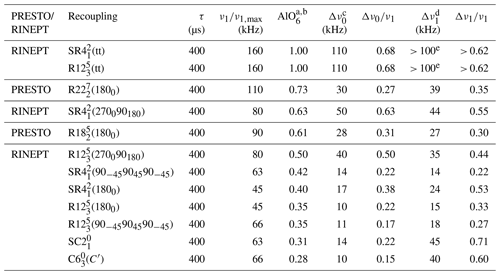
a AlO6 signal normalized to that with 1H → 27Al RINEPT-CWc-(tt). b The relative error bars were determined from the S N, for the AlO6 signal intensity, and they are equal to ±0.03. c FWHM (full width at half maximum) of the robustness to offset. d FWHM of the robustness to rf field. e Only a lower bound of rf field could be determined due to probe rf specifications (Fig. 4).
Table 2Comparison of the performances of 1H → 27Al RINEPT-CWc and PRESTO transfers with AlPO4-14 at νR=20 kHz.
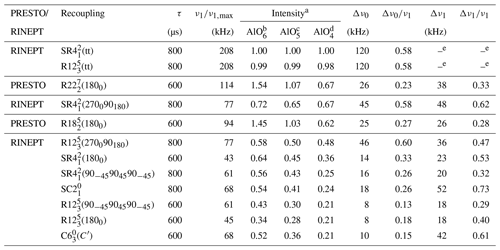
a Intensities of AlO6, AlO5 and AlO4 resonances normalized to their intensities with 1H → 27Al RINEPT-CWc-(tt). The relative errors for the signal intensities are b ± 0.02, c ±0.03 and d ±0.01, for AlO6, AlO5 and AlO4, respectively. e FWHM of the robustness to rf field was not measured for RINEPT-(tt) or RINEPT-(tt) (Fig. S2).
1H → 27Al RINEPT-CWc and PRESTO-III experiments on γ-alumina and AlPO4-14 were performed with a 1.3 mm MAS probe spinning at νR=20 (to test the schemes with large rf field requirement) or 62.5 kHz. The tested recoupling schemes are listed in Tables 1 and 2 for νR=20 kHz and Tables 3 and 4 for νR=62.5 kHz. The rf field of the 1H and π pulses, which do not belong to the recoupling scheme, was equal to 208 kHz, that of the continuous-wave irradiation to 147 kHz, and the 27Al CT-selective one for and π pulses to 10 kHz. The defocusing and refocusing delays τ are given in Tables 1 to 4. The pulses on the 1H channel were applied on resonance, whereas those on 27Al channel were applied (i) on resonance with AlO6 signal of γ-alumina in Figs. 4 and 7, Tables 1 and 3, and in Figs. 5 and 8 when the offset is null; (ii) on resonance with AlO4 signal of AlPO4-14 in Figs. S2 and S4, Tables 2 and 4 as well as in Figs. S3 and S5 when the offset is null; and (iii) in the middle of the AlO4 and AlO6 peaks for the 1D spectra shown in Figs. 3 and 6. These differences in offset explain some changes in the relative efficiencies of the recoupling between the figures. These 1D spectra resulted from averaging 64 transients with a relaxation delay of 1 s. The 27Al isotropic chemical shifts were referenced at 0 ppm to 1 mol L−1 [Al(H2O)6]3+ solution.
Table 3Comparison of the performances of 1H → 27Al RINEPT-CWc and PRESTO transfers using various recouplings for the AlO6 signal of γ-alumina at νR=62.5 kHz.
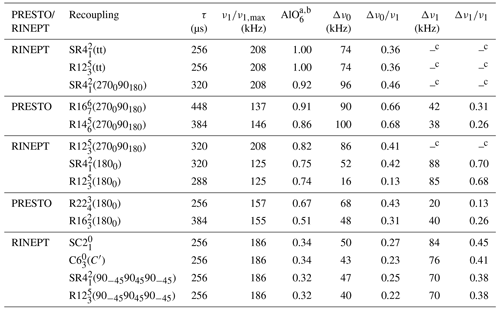
a AlO6 signal normalized to that with 1H → 27Al RINEPT-CWc-(tt). b The relative error on AlO6 signal intensity is ±0.08. c FWHM of the robustness to rf field was not measured for RINEPT-(tt) or RINEPT-(tt) (Fig. 7).
Table 4Comparison of the performances of 1H → 27Al RINEPT-CWc and PRESTO transfers using various recouplings for AlPO4-14 at νR=62.5 kHz.
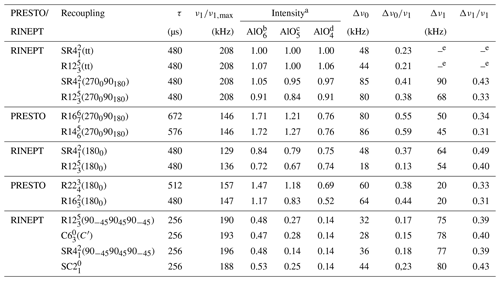
a Intensities of AlO6, AlO5 and AlO4 resonances normalized to their intensities with 1H → 27Al RINEPT-CWc-(tt). The relative errors for the signal intensities are b ±0.04, c ±0.06 and d ±0.02, for AlO6, AlO5 and AlO4, respectively. e FWHM of the robustness to rf field was not measured for RINEPT-(tt) or RINEPT-(tt) (Fig. S4).
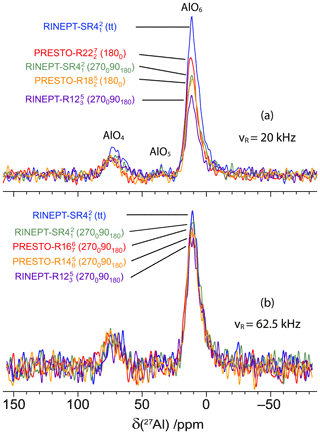
Figure 3The 27Al 1D spectra of γ-alumina at 18.8 T with νR=20 kHz (a) and 62.5 kHz (b) acquired using 1H → 27Al transfers with RINEPT-CWc and , (270090180) and (270090180), or PRESTO and (a) (1800) or (1800), or (b) (270090180) and (270090180). The τ delays and rf fields were fixed to their optimum values given in Tables 1 and 3.
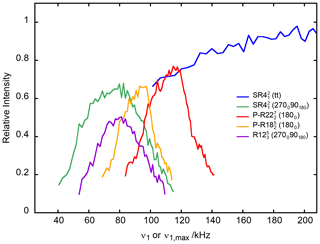
Figure 4The 27AlO6 on-resonance signal of γ-alumina at νR=20 kHz as a function of ν1 or for PRESTO-(1800) and PRESTO-(1800) as well as RINEPT-CWc-(tt), RINEPT-(270090180) and RINEPT- (270090180). For each curve, τ was fixed to its optimum value given in Table 1.
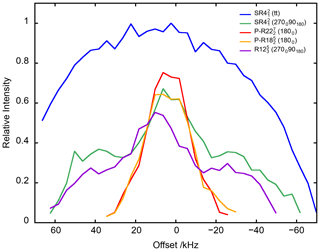
Figure 5The 27AlO6 signal of γ-alumina at νR=20 kHz as a function of offset for PRESTO-(1800) and PRESTO-(1800) as well as RINEPT-CWc-(tt), RINEPT-(270090180) and RINEPT-(270090180). For each curve, τ and ν1 or were fixed to their optimum values given in Table 1.
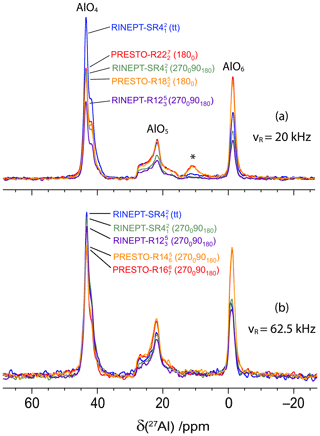
Figure 6The 27Al 1D spectra of AlPO4-14 at 18.8 T with νR=20 kHz (a) and 62.5 kHz (b) acquired using 1H → 27Al transfers with RINEPT-CWc and , (270090180) and (270090180), or PRESTO and (a) (1800) and (1800), or (b) (270090180) and (270090180). The τ delays and rf fields were fixed to their optimal values given in Tables 2 and 4. The resonance at ca. 11 ppm in panel (a) is due to an impurity.
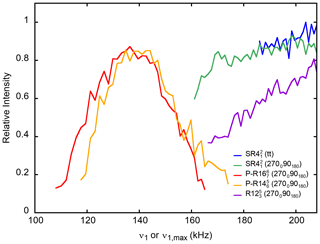
Figure 7The 27AlO6 on-resonance signal of γ-alumina at νR=62.5 kHz as a function of ν1 or for PRESTO-(270090180) and PRESTO-(270090180) as well as RINEPT-CWc-(tt), RINEPT-(270090180) and RINEPT-(270090180). For each curve, τ was fixed to its optimum value given in Table 3.
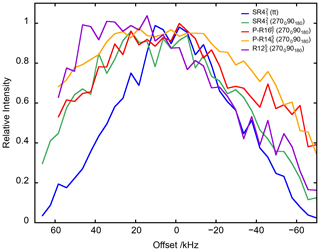
Figure 8The 27AlO6 signal of γ-alumina at νR=62.5 kHz as a function of offset for PRESTO-(270090180) and PRESTO-(270090180) as well as RINEPT-CWc-(tt), RINEPT-(270090180) and RINEPT-(270090180). For each curve, τ and ν1 or were fixed to their optimum values given in Table 3.
We also measured the decay of the transverse proton magnetization of AlPO4-14 during a spin echo sequence, in which the refocusing π pulse was identical to that used in the defocusing part of the RINEPT-CWc sequences (Fig. 1b). This decay was measured at νR=20 and 62.5 kHz either without any recoupling or by applying a recoupling built from (1800), (270090180) and (tt) pulses during the delays of the spin echo sequence. The rf fields during the recoupling two blocks were equal to their optimal values given in Tables 2 and 4.
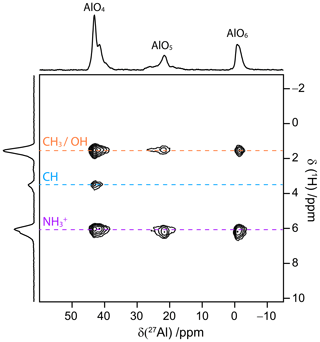
We also acquired several 2D 1H → 27Al D-HETCOR spectra of AlPO4-14 using RINEPT-CWc- with (1800), (270090180) and (tt) pulses as well as PRESTO-(270090180). These 2D spectra were acquired using a non-uniform sampling (NUS) with an exponentially biased sampling retaining 25 % of the points with respect to uniform sampling. The 2D spectra resulted from eight transients for each of the 500 t1 increments with a recycle delay of 1 s, i.e., an acquisition time of 72 min.
4.2 Optimal adiabatic recoupling
Figure 2e and f show the efficiency of the 1H → 15N RINEPT-(tt) transfer for histidine as a function of the and ratios for νR = 40 or 62.5 kHz, respectively. These experimental data indicate that at higher MAS frequencies, an efficient adiabatic recoupling can be achieved for lower and ratios. This result agrees with the numerical simulations of Fig. 2b and d.
4.3 PRESTO and RINEPT performances for νR=20 kHz
4.3.1 γ-alumina
The 1D spectra of γ-alumina acquired using 1H → 27Al RINEPT and PRESTO sequences, shown in Fig. 3, exhibit two resonances at 70 and 10 ppm, assigned to tetra- (AlO4) and hexa-coordinated (AlO6) resonances, respectively (Morris and Ellis, 1989). The signal of penta-coordinated (AlO5) sites, which are mainly located in the first surface layer, is barely detected because of the lack of sensitivity of conventional solid-state NMR spectroscopy (Lee et al., 2014). The most intense peak, AlO6, was used to compare the transfer efficiencies of RINEPT and PRESTO sequences with different recoupling schemes. Table 1 lists the measured performances of 1H → 27Al RINEPT-CWc and PRESTO transfers using various recoupling for γ-alumina at νR=20 kHz. We notably compared the PRESTO sequences using (1800) and (1800) recoupling with the RINEPT-CWc scheme using and with single (1800), composite (270090180), and (90−45904590−45) or (tt) adiabatic pulses. A low transfer efficiency was obtained for RINEPT-CWc-(90024090900) because of its low scaling factor, κ = 0.131; hence, its performances are not reported in Table 1. We also tested the recoupling schemes based on the symmetry , corresponding to the sequence with a basic element C = (9045901359045902259031590225) or built from C′ = (9030901209030902409033090240). These basic elements, which derive from (90−45904590−45), have recently been proposed (Perras et al., 2019). As seen in Table 1 and Fig. 3a, the sequences yielding the highest transfer efficiencies are by decreasing order RINEPT-CWc with (tt) or (tt) > PRESTO-(1800) > RINEPT-CWc-(270090180) ≈ PRESTO-(1800) > RINEPT-CWc-(270090180). Figures 4 and 5 display the signal intensity of these sequences as a function of the rf field amplitude and offset, respectively.
The highest transfer efficiencies are obtained with the RINEPT-CWc sequence incorporating a (tt) adiabatic pulse. This recoupling also leads to the highest robustness to offset and rf inhomogeneity, and (tt) and (tt) yield identical transfer efficiency and robustness. Hence, the three-step multiple-quantum super-cycle of the symmetry does not improve the robustness in the case of a (tt) basic element. However, these recoupling schemes require maximum rf fields of 160 kHz, which may exceed the rf power specifications of most 3.2 mm MAS probes.
The PRESTO sequences using (1800) and (1800) recoupling also result in good transfer efficiencies but lower than RINEPT-CWc-(tt). However, they use rf fields of 5.5 and 4.5, which are compatible with the specifications of 3.2 mm MAS probes. The higher transfer efficiency of (1800) with respect to (1800) stems from its weaker second-order cross terms between 1H–1H interactions (Table S1).
The efficiency of the RINEPT-CWc-(270090180) sequence, with ν1=4νR, is comparable to that of PRESTO-(1800) but with a higher robustness to offset and rf inhomogeneity. We can notice that amplitude modulated recoupling schemes, for which the phase shifts are equal to 180∘, such as (270090180) and (1800), exhibit a high robustness to rf field maladjustments (Fig. 5) (Carravetta et al., 2000). The use of (270090180) composite pulses with symmetry, instead of single π pulses, improves its transfer efficiency as well as its robustness to offset and rf field inhomogeneity.
In summary, for νR=20 kHz in γ-alumina, the RINEPT-CWc-(270090180) sequence achieves efficient and robust transfers of magnetization from protons to 27Al nuclei using a moderate rf field of ν1=4νR. For 1H spectra with a width smaller than 20 kHz and MAS probes with a good rf homogeneity, PRESTO-(1800) can result in slightly higher transfer efficiencies.
4.3.2 AlPO4-14
Figure 6a shows the 1H → 27Al RINEPT and PRESTO 1D spectra of AlPO4-14 recorded with νR=20 kHz. They exhibit three 27Al resonances at 43, 21 and −2 ppm assigned to AlO4, AlO5 and AlO6 sites, respectively (Ashbrook et al., 2008) The AlO5 and AlO6 sites are directly bonded to OH groups. The 1H MAS spectrum is shown in Fig. S1. According to the literature, the 27AlO4 signal subsumes the resonances of two AlO4 sites with quadrupolar coupling constants CQ = 1.7 and 4.1 MHz, whereas those of AlO5 and AlO6 sites are equal to 5.6 and 2.6 MHz, respectively (Fernandez et al., 1996; Antonijevic et al., 2006). The 1H–1H dipolar couplings within the isopropylamine template molecule are larger than in γ-alumina. We used the most intense peak, AlO4, to compare the 1H → 27Al transfer efficiencies of RINEPT-CWc and PRESTO sequences with different recoupling schemes, and the results are given in Table 2. The six sequences yielding the highest transfer efficiencies are the same as for γ-alumina and their relative efficiencies are comparable for the AlO4 peak of AlPO4-14 and the AlO6 signal of γ-alumina.
Nevertheless, the rf requirement of the (tt) and (tt) schemes is higher for AlPO4-14 than for γ-alumina because of the larger 1H–1H dipolar couplings, in agreement with the numerical simulations of Fig. 2a–c. This rf requirement prevents the use of these adiabatic recoupling schemes at νR=20 kHz with most 3.2 mm MAS probes. That of the other sequences and their robustness to offset and rf field homogeneity are similar for both samples (Table 2 and Figs. S2 and S3).
In the case of AlPO4-14, PRESTO yields a higher efficiency than RINEPT for AlO5 and AlO6, contrary to the AlO4 resonance, since (i) these Al sites are directly bonded to OH groups and (ii) (1800) and (1800) schemes are subject to dipolar truncation (Sect. 2.1.1), which prevents to transfer the 1H magnetization of these OH groups to 27AlO4 nuclei.
Hence, at νR=20 kHz, for both AlPO4-14 and γ-alumina, the RINEPT-CWc-(270090180) and PRESTO-(1800) sequences are the best choices to transfer the 1H magnetization to 27Al nuclei.
4.4 PRESTO and RINEPT performances for νR=62.5 kHz
Similar comparisons of the performances of the various RINEPT-CWc and PRESTO sequences were performed for γ-alumina and AlPO4-14 at νR=62.5 kHz.
4.4.1 γ-alumina
The corresponding data for γ-alumina are given in Table 3. The sequences yielding the highest transfer efficiencies are by decreasing order: RINEPT-CWc with (tt) or (tt) > RINEPT-CWc-(270090180) ≈ PRESTO-(270090180) > PRESTO-(270090180) > RINEPT-CWc-(270090180).
The nominal rf requirements of the RINEPT sequences using adiabatic or (270090180) composite π pulses correspond to (313 kHz: Fig. 2d) or 4νR (250 kHz), which exceed the specifications of our 1.3 mm MAS probe, and the sequences were tested only up to kHz (Fig. 7). This suboptimal rf field may limit the transfer efficiencies of these sequences.
The PRESTO-(270090180) and PRESTO-(270090180) sequences yield transfer efficiencies comparable to those of RINEPT-CWc-(270090180) but with a significantly lower rf field, ν1≈137 kHz ≈2.3νR. Furthermore, the robustness to offset of these PRESTO sequences is comparable to that of RINEPT-CWc-(270090180) (Fig. 8). PRESTO-(1800) and PRESTO-(1800) sequences with a small phase shift of 2ϕ≤52∘ are less efficient, because they are sensitive to rf inhomogeneity.
4.4.2 AlPO4-14
In the case of AlPO4-14, the relative transfer efficiencies for 27AlO4 species follow a similar order as for γ-alumina, except that the transfer efficiencies of PRESTO-(270090180) and PRESTO-(270090180) are significantly lower than that of RINEPT-CWc-(270090180) (Table 4). This decreased efficiency of the PRESTO schemes for AlO4 stems notably from the dipolar truncation, which prevents the transfer of magnetization from the OH groups bonded to AlO5 and AlO6 sites to AlO4, since these 27AlO4 nuclei are significantly more distant from protons (see Table S5). Furthermore, the amplitude-modulated (270090180) recoupling benefits from a higher robustness to rf field inhomogeneity than the PRESTO schemes (Fig. S4). Conversely, the robustness to offset of these three sequences are comparable (Fig. S5), whereas the rf requirements of (270090180) and (270090180) are much lower than that of (270090180).
In summary, at νR=62.5 kHz, for both γ-alumina and isopropylamine-templated AlPO4-14, PRESTO-(270090180) and RINEPT-CWc-(270090180) are the best methods to transfer the polarization of protons to quadrupolar nuclei. However, the first sequence requires a much lower rf field than the second does.
4.5 Decay of transverse 1H magnetization during recoupling
We also measured the decay of the 1H transverse magnetization during a spin echo experiment, in which the refocusing π pulse was the composite one employed in the defocusing part of the RINEPT-CW sequence shown in Fig. 1b. We performed these experiments on AlPO4-14 since the 1H–1H dipolar interactions are larger in this sample than in γ-alumina. This decay was measured either in the absence of any recoupling or under a recoupling built from (1800), (270090180) or (tt) inversion element. The three 1H signals featured a mono-exponential decay with a time constant reported in Table 5.
Table 5The 1H values of AlPO4-14 without recoupling or with recoupling built from (1800), (270090180) or (tt) inversion elements. The estimated error bars are equal to 7 %.
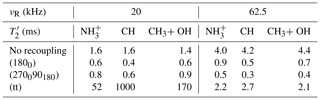
At νR=20 kHz, the constants are significantly shorter under (1800) and (270090180) than without recoupling. This faster decay can stem from the reintroduction of 1H–1H dipolar interactions in the second- and higher-order terms of the AH by the recoupling as well as the effect of pulse transients (Wittmann et al., 2016). Conversely, the constants under (tt) are much longer than without recoupling, showing that the adiabatic pulses using large rf field efficiently decouple the 1H–1H dipolar interactions, whereas the continuous variation of the phase and amplitude during these pulses minimizes the transients.
At νR=62.5 kHz, the constants without recoupling are lengthened with respect to those at νR=20 kHz since faster MAS better averages the 1H–1H dipolar interactions (Mao et al., 2009). Conversely, the constants under (270090180) recoupling are shorter at νR=62.5 than at 20 kHz. This counterintuitive reduction may stem from the shorter pulse lengths at νR=62.5 kHz, which result in a larger number of transients. Indeed, the recoupling time, τ, only depends on the sample; hence, the number of transients is proportional to νR, because the recoupling sequences are rotor synchronized. Moreover, it also increases with the use of composite pulses and as a result there are 6.25 times more transients at νR=62.5 kHz and (2700,90180) pulses than at 20 kHz MAS and (1800) pulses. Additionally, the rf power increases with the spinning speed and the use of composite pulses, and then also the amplitude of the transients. For the same reason, the constants under (1800) are only slightly longer at high MAS frequency. The constants under (tt) recoupling are much shorter at νR=62.5 than at 20 kHz, because the adiabaticity criterion is not fulfilled at νR=62.5 kHz; hence, the elimination of 1H–1H dipolar interactions is less effective (Figs. 2f and S4).
4.6 2D 1H–27Al D-HETCOR of AlPO4-14
Figure 9 demonstrates the possibility to acquire 2D 1H–27Al D-HETCOR spectra using RINEPT-CWc-(2700,90180) transfer at νR=62.5 kHz. This spectrum was recorded using a NUS scheme retaining 25 % of the t1 points, which would be acquired using uniform sampling. In this spectrum, the CH proton only correlates with the AlO4 site since it is too distant from AlO5 and AlO6 sites (see Table S5). The other two 1H signals correlate with the three Al environments. Similar 2D spectra (not shown) were acquired using RINEPT-CWc transfer based on (1800) and (tt) recoupling as well as PRESTO-(270090180). Their skyline projections are shown in Figs. S6 and S7.
In this work, we have introduced novel symmetry-based heteronuclear dipolar recoupling schemes, which can be incorporated into the RINEPT and PRESTO sequences to transfer the magnetization from protons to half-integer quadrupolar nuclei at νR=20 or 62.5 kHz. These new recouplings have been compared to the existing ones. We have shown that the RINEPT-CWc-(tt) sequence with adiabatic pulses, which produces efficient and robust transfers at νR≈10–15 kHz (Nagashima et al., 2020), requires rf fields incompatible with the specifications of most MAS probes for νR≥20 kHz. Conversely, the introduced RINEPT-CWc-(270090180) and PRESTO-(1800) techniques with rf fields of ca. 4νR and 5.5νR, respectively, are the methods of choice at νR=20 kHz to transfer the magnetization from protons to quadrupolar nuclei. At νR=62.5 kHz, the RINEPT-CWc-(270090180) and PRESTO-(270090180) sequences with rf requirements of ca. 4νR and 2.3νR, respectively, result in the most robust and efficient transfers. At both MAS frequencies, the RINEPT and PRESTO techniques complement each other since the latter is dipolar truncated, whereas the former is not. As a result, the RINEPT sequences must be chosen to observe simultaneously protonated and unprotonated sites, whereas the PRESTO schemes can be employed for the selective observation of quadrupolar nuclei in proximity to protons. These techniques are expected to be useful for transferring the DNP-enhanced magnetization of protons to quadrupolar nuclei in indirect MAS DNP experiments at νR≥20 kHz, notably used at high magnetic fields (Nagashima et al., 2021, 2020; Rankin et al., 2019; Berruyer et al., 2020). We also show that they can be used to correlate the NMR signals of protons and quadrupolar nuclei at high MAS frequencies.
The raw data are available on the Zenodo site at https://doi.org/10.5281/zenodo.4896852 (Gómez et al., 2021).
The supplement related to this article is available online at: https://doi.org/10.5194/mr-2-447-2021-supplement.
JSG, AGMR and JT carried out the NMR experiments on γ-alumina and AlPO4-14. YT performed the spin dynamics simulations and carried out the NMR experiments on L-histidine ⋅ HCl. OL derived average Hamiltonian theory for the investigated recoupling sequences. HN and FP contributed to the analysis and interpretation of the results. OL and JPA wrote the article. All the authors contributed to the editing of the article.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Geoffrey Bodenhausen Festschrift”. It is not associated with a conference.
This article is dedicated to Francis Taulelle, our friend, who passed away very recently. The Chevreul Institute (FR 2638), Ministère de l'Enseignement Supérieur, de la Recherche et de l'Innovation, Hauts-de-France Region, and FEDER are acknowledged for supporting and funding partially this work. Olivier Lafon acknowledges financial support from Institut Universitaire de France (IUF) and contract ANR-18-CE08-0015-01 (ThinGlass). Frédérique Pourpoint acknowledges financial support from I-site contract OPE-2019-0043 (5400-MOFFIN).
This research has been supported by the IR-RMN-THC FR-3050 CNRS, the European Union's Horizon 2020 research and innovation program (EUSMI, grant no. 731019), Institut Universitaire de France (IUF), Agence Nationale de la Recherche (contract ANR-18-CE08-0015-01, ThinGlass), and I-site UNLE (contract OPE-2019-0043, 5400-MOFFIN).
This paper was edited by Fabien Ferrage and reviewed by one anonymous referee.
Amoureux, J.-P. and Pruski, M.: Theoretical and experimental assessment of single- and multiple-quantum cross-polarization in solid state NMR, Molec. Phys., 100, 1595–1613, https://doi.org/10.1080/00268970210125755, 2002.
Antonijevic, S., Ashbrook, S. E., Biedasek, S., Walton, R. I., Wimperis, S., and Yang, H.: Dynamics on the Microsecond Timescale in Microporous Aluminophosphate AlPO-14 as Evidenced by 27Al MQMAS and STMAS NMR Spectroscopy, J. Am. Chem. Soc., 128, 8054–8062, https://doi.org/10.1021/ja057682g, 2006.
Ashbrook, S. E. and Sneddon, S.: New Methods and Applications in Solid-State NMR Spectroscopy of Quadrupolar Nuclei, J. Am. Chem. Soc., 136, 15440–15456, https://doi.org/10.1021/ja504734p, 2014.
Ashbrook, S. E. and Wimperis, S.: Spin-locking of half-integer quadrupolar nuclei in nuclear magnetic resonance of solids: Second-order quadrupolar and resonance offset effects, J. Chem. Phys., 131, 194509, https://doi.org/10.1063/1.3263904, 2009.
Ashbrook, S. E., Cutajar, M., Pickard, C. J., Walton, R. I., and Wimperis, S.: Structure and NMR assignment in calcined and as-synthesized forms of AlPO-14: a combined study by first-principles calculations and high-resolution 27Al–31PMAS NMR correlation, Phys. Chem. Chem. Phys., 10, 5754–5764, https://doi.org/10.1039/B805681A, 2008.
Bak, M. and Nielsen, N. C.: REPULSION, A Novel Approach to Efficient Powder Averaging in Solid-State NMR, J. Magn. Reson., 125, 132–139, https://doi.org/10.1006/jmre.1996.1087, 1997.
Bak, M., Rasmussen, J. T., and Nielsen, N. C.: SIMPSON: a general simulation program for solid-state NMR spectroscopy. J. Magn. Reson., 147, 296–330, https://doi.org/10.1006/jmre.2000.2179, 2000.
Barrie, P. J.: Distorted powder lineshapes in 27Al CP/MAS NMR spectroscopy of solids, Chem. Phys. Lett., 208, 486–490, https://doi.org/10.1016/0009-2614(93)87177-5, 1993.
Bayro, M. J., Huber, M., Ramachandran, R., Davenport, T. C., Meier, B. H., Ernst, M., and Griffin, R. G.: Dipolar truncation in magic-angle spinning NMR recoupling experiments, J. Chem. Phys., 130, 114506, https://doi.org/10.1063/1.3089370, 2009.
Berruyer, P., Björgvinsdóttir, S., Bertarello, A., Stevanato, G., Rao, Y., Karthikeyan, G., Casano, G., Ouari, O., Lelli, M., Reiter, C., Engelke, F., and Emsley, L.: Dynamic Nuclear Polarization Enhancement of 200 at 21.15 T Enabled by 65 kHz Magic Angle Spinning, J. Phys. Chem. Lett., 11, 8386–8391, https://doi.org/10.1021/acs.jpclett.0c02493, 2020.
Blanc, F., Sperrin, L., Jefferson, D. A., Pawsey, S., Rosay, M., and Grey, C. P.: Dynamic Nuclear Polarization Enhanced Natural Abundance 17O Spectroscopy, J. Am. Chem. Soc., 135, 2975–2978, https://doi.org/10.1021/ja4004377, 2013.
Brinkmann, A. and Edén, M.: Second order average Hamiltonian theory of symmetry-based pulse schemes in the nuclear magnetic resonance of rotating solids: Application to triple-quantum dipolar recoupling, J. Chem. Phys., 120, 11726–11745, https://doi.org/10.1063/1.1738102, 2004.
Brinkmann, A. and Kentgens, A. P. M.: Proton-Selective 17O- 1H Distance Measurements in Fast Magic-Angle-Spinning Solid-State NMR Spectroscopy for the Determination of Hydrogen Bond Lengths, J. Am. Chem. Soc., 128, 14758–14759, https://doi.org/10.1021/ja065415k, 2006a.
Brinkmann, A. and Kentgens, A. P. M.: Sensitivity Enhancement and Heteronuclear Distance Measurements in Biological 17O Solid-State NMR, J. Phys. Chem. B, 110, 16089–16101, https://doi.org/10.1021/jp062809p, 2006b.
Brinkmann, A. and Levitt, M. H.: Symmetry principles in the nuclear magnetic resonance of spinning solids: Heteronuclear recoupling by generalized Hartmann-Hahn sequences, J. Chem. Phys., 115, 357–384, https://doi.org/10.1063/1.1377031, 2001.
Brinkmann, A., Edén, M., and Levitt, M. H.: Synchronous helical pulse sequences in magic-angle spinning nuclear magnetic resonance: double quantum recoupling of multiple-spin systems, J. Chem. Phys.,112, 8539–8554, https://doi.org/10.1063/1.481458, 2000.
Carravetta, M., Edén, M., Zhao, X., Brinkmann, A., and Levitt, M. H.: Symmetry principles for the design of radiofrequency pulse sequences in the nuclear magnetic resonance of rotating solids, Chem. Phys. Lett., 321, 205–215, https://doi.org/10.1016/S0009-2614(00)00340-7, 2000.
Chen, J., Wu, X.-P., Hope, M. A., Qian, K., Halat, D. M., Liu, T., Li, Y., Shen, L., Ke, X., Wen, Y., Du, J.-H., Magusin, P. C. M. M., Paul, S., Ding, W., Gong, X.-Q., Grey, C. P., and Peng, L.: Polar surface structure of oxide nanocrystals revealed with solid-state NMR spectroscopy, Nat. Commun., 10, 1–10, https://doi.org/10.1038/s41467-019-13424-7, 2019.
Ding, S. W. and Mcdowell, C. A.: Theoretical Calculations of the CPMAS Spectral Lineshapes of Half-Integer Quadrupole Systems, J. Mag. Reson. A, 114, 80–87, https://doi.org/10.1006/jmra.1995.1108, 1995.
Duong, N. T., Trébosc, J., Lafon, O., and Amoureux, J.-P.: Improved sensitivity and quantification for 29Si NMR experiments on solids using UDEFT (Uniform Driven Equilibrium Fourier Transform), Solid State Nucl. Magn. Reson., 100, 52–62, https://doi.org/10.1016/j.ssnmr.2019.03.007, 2019.
Fernandez, C., Amoureux, J. P., Chezeau, J. M., Delmotte, L., and Kessler, H.: 27Al MAS NMR characterization of AlPO4-14 enhanced resolution and information by MQMAS Dr. Hellmut G. Karge on the occasion of his 65th birthday, Microporous Mater., 6, 331–340, https://doi.org/10.1016/0927-6513(96)00040-5, 1996.
Freeman, R., Kempsell, S. P., and Levitt, M. H.: Radiofrequency pulse sequences which compensate their own imperfections, J. Magn. Reson., 38, 453–479, https://doi.org/10.1016/0022-2364(80)90327-3, 1980.
Gansmüller, A., Simorre, J.-P., and Hediger, S.: Windowed R-PDLF recoupling: A flexible and reliable tool to characterize molecular dynamics, J. Magn. Reson., 234, 154–164, https://doi.org/10.1016/j.jmr.2013.06.017, 2013.
Garwood, M. and DelaBarre, L.: The Return of the Frequency Sweep: Designing Adiabatic Pulses for Contemporary NMR, J. Magn. Reson., 153, 155–177, https://doi.org/10.1006/jmre.2001.2340, 2001.
Giovine, R., Trébosc, J., Pourpoint, F., Lafon, O., and Amoureux, J.-P.: Magnetization transfer from protons to quadrupolar nuclei in solid-state NMR using PRESTO or dipolar-mediated refocused INEPT methods, J. Magn. Reson., 299, 109–123, https://doi.org/10.1016/j.jmr.2018.12.016, 2019.
Gómez, J. S., Rankin, A. G. M., Trébosc, J., Pourpoint, F., Tsutsumi, Y., Nagashima, H., and Lafon, O.: Improved NMR transfer of magnetization from protons to half-integer spin quadrupolar nuclei at moderate and high MAS frequencies, Zenodo [data set], https://doi.org/10.5281/zenodo.4896852, 2021.
Harris, R. K. and Nesbitt, G. J.: Cross polarization for quadrupolar nuclei – Proton to sodium-23, J. Magn. Reson., 78, 245–256, https://doi.org/10.1016/0022-2364(88)90268-5, 1988.
Hayashi, S. and Hayamizu, K.: Line shapes in CP/MAS NMR spectra of half-integer quadrupolar nuclei, Chem. Phys. Lett., 203, 319–324, https://doi.org/10.1016/0009-2614(93)85575-9, 1993.
Hope, M. A., Halat, D. M., Magusin, P. C. M. M., Paul, S., Peng, L., and Grey, C. P.: Surface-selective direct 17O DNP NMR of CeO2 nanoparticles, Chem. Commun., 53, 2142–2145, https://doi.org/10.1039/C6CC10145C, 2017.
Hu, B., Delevoye, L., Lafon, O., Trébosc, J., and Amoureux, J. P.: Double-quantum NMR spectroscopy of 31P species submitted to very large CSAs, J. Magn. Reson., 200, 178–88, https://doi.org/10.1016/j.jmr.2009.06.020, 2009.
Hwang, S.-J., Chen, C.-Y., and Zones, S. I.: Boron Sites in Borosilicate Zeolites at Various Stages of Hydration Studied by Solid State NMR Spectroscopy, J. Phys. Chem. B, 108, 18535–18546, https://doi.org/10.1021/jp0476904, 2004.
Kervern, G., Pintacuda, G., and Emsley, L.: Fast adiabatic pulses for solid-state NMR of paramagnetic systems, Chem. Phys. Lett., 435, 157–162, https://doi.org/10.1016/j.cplett.2006.12.056, 2007.
Lee, D., Duong, N. T., Lafon, O., and De Paëpe, G.: Primostrato Solid-State NMR Enhanced by Dynamic Nuclear Polarization: Pentacoordinated Al3+ Ions Are Only Located at the Surface of Hydrated γ-Alumina, J. Phys. Chem. C, 118, 25065–25076, https://doi.org/10.1021/jp508009x, 2014.
Lee, D., Leroy, C., Crevant, C., Bonhomme-Coury, L., Babonneau, F., Laurencin, D., Bonhomme, C., and Paëpe, G. D.: Interfacial Ca2+ environments in nanocrystalline apatites revealed by dynamic nuclear polarization enhanced 43Ca NMR spectroscopy, Nat. Commun., 8, 14104, https://doi.org/10.1038/ncomms14104, 2017.
Levitt, M. H.: Symmetry-based pulse sequences in magic-angle spinning solid-state NMR, in: Encyclopedia of Nuclear Magnetic Resonance. Volume 9, Advances in NMR, edited by: Grant, D. M. and Harris, R. K., Wiley, Chichester, UK, 165–196, 2002.
Levitt, M. H. and Freeman, R.: NMR population inversion using a composite pulse, J. Magn. Reson., 33, 473–476, https://doi.org/10.1016/0022-2364(79)90265-8, 1979.
Li, W., Wang, Q., Xu, J., Aussenac, F., Qi, G., Zhao, X., Gao, P., Wang, C., and Deng, F.: Probing the surface of γ-Al2O3 by oxygen-17 dynamic nuclear polarization enhanced solid-state NMR spectroscopy, Phys. Chem. Chem. Phys., 20, 17218–17225, https://doi.org/10.1039/C8CP03132K, 2018.
Liang, L., Hou, G., and Bao, X.: Measurement of proton chemical shift anisotropy in solid-state NMR spectroscopy, Solid State Nucl. Magn. Reson., 93, 16–28, https://doi.org/10.1016/j.ssnmr.2018.04.002, 2018.
Lu, X., Lafon, O., Trébosc, J., Tricot, G., Delevoye, L., Méar, F., Montagne, L., and Amoureux, J. P.: Observation of proximities between spin- and quadrupolar nuclei: which heteronuclear dipolar recoupling method is preferable?, J. Chem. Phys.,137, 144201, https://doi.org/10.1063/1.4753987, 2012.
Madhu, P. K., Zhao, X., and Levitt, M. H.: High-resolution 1H NMR in the solid state using symmetry-based pulse sequences, Chem. Phys. Lett., 346, 142–148, https://doi.org/10.1016/S0009-2614(01)00876-4, 2001.
Mao, K., Wiench, J. W., Lin, V. S.-Y., and Pruski, M.: Indirectly detected through-bond chemical shift correlation NMR spectroscopy in solids under fast MAS: Studies of organic–inorganic hybrid materials, J. Magn. Reson., 196, 92–95, https://doi.org/10.1016/j.jmr.2008.10.010, 2009.
Martineau, C., Bouchevreau, B., Taulelle, F., Trébosc, J., Lafon, O., and Amoureux, J. P.: High-resolution through-space correlations between spin- and half-integer quadrupolar nuclei using the MQ-D-R-INEPT NMR experiment, Phys. Chem. Chem. Phys., 14, 7112–7119, https://doi.org/10.1039/C2CP40344G, 2012.
Morris, H. D. and Ellis, P. D.: Aluminum-27 cross polarization of aluminas. The NMR spectroscopy of surface aluminum atoms, J. Am. Chem. Soc., 111, 6045–6049, https://doi.org/10.1021/ja00198a012, 1989.
Nagashima, H., Lilly Thankamony, A. S., Trébosc, J., Montagne, L., Kerven, G., Amoureux, J.-P., and Lafon, O.: Observation of proximities between spin- and quadrupolar nuclei in solids: Improved robustness to chemical shielding using adiabatic symmetry-based recoupling, Solid State Nucl. Magn. Reson., 94, 7–19, https://doi.org/10.1016/j.ssnmr.2018.07.001, 2018.
Nagashima, H., Trébosc, J., Kon, Y., Sato, K., Lafon, O., and Amoureux, J.-P.: Observation of Low-γ Quadrupolar Nuclei by Surface-Enhanced NMR Spectroscopy, J. Am. Chem. Soc., 142, 10659–10672, https://doi.org/10.1021/jacs.9b13838, 2020.
Nagashima, H., Trébosc, J., Kon, Y., Lafon, O., and Amoureux, J.-P.: Efficient transfer of DNP-enhanced 1H magnetization to half-integer quadrupolar nuclei in solids at moderate spinning rate, Magn. Reson. Chem., https://doi.org/10.1002/mrc.5121, online first, 2021.
Pandey, M. K., Malon, M., Ramamoorthy, A., and Nishiyama, Y.: Composite-180∘ pulse-based symmetry sequences to recouple proton chemical shift anisotropy tensors under ultrafast MAS solid-state NMR spectroscopy, J. Magn. Reson., 250, 45–54, https://doi.org/10.1016/j.jmr.2014.11.002, 2015.
Peng, L., Huo, H., Liu, Y., and Grey, C. P.: 17O Magic Angle Spinning NMR Studies of Brønsted Acid Sites in Zeolites HY and HZSM-5, J. Am. Chem. Soc., 129, 335–346, https://doi.org/10.1021/ja064922z, 2007.
Perras, F. A., Kobayashi, T., and Pruski, M.: Natural Abundance 17O DNP Two-Dimensional and Surface-Enhanced NMR Spectroscopy, J. Am. Chem. Soc., 137, 8336–8339, https://doi.org/10.1021/jacs.5b03905, 2015a.
Perras, F. A., Kobayashi, T., and Pruski, M.: PRESTO polarization transfer to quadrupolar nuclei: implications for dynamic nuclear polarization, Phys. Chem. Chem. Phys., 17, 22616–22622, https://doi.org/10.1039/C5CP04145G, 2015b.
Perras, F. A., Chaudhary, U., Slowing, I. I., and Pruski, M.: Probing Surface Hydrogen Bonding and Dynamics by Natural Abundance, Multidimensional, 17O DNP-NMR Spectroscopy, J. Phys. Chem. C, 120, 11535–11544, https://doi.org/10.1021/acs.jpcc.6b02579, 2016.
Perras, F. A., Wang, Z., Naik, P., Slowing, I. I., and Pruski, M.: Natural Abundance 17O DNP NMR Provides Precise O-H Distances and Insights into the Brønsted Acidity of Heterogeneous Catalysts, Angew. Chem. Int. Ed., 56, 9165–9169, https://doi.org/10.1002/anie.201704032, 2017.
Perras, F. A., Goh, T. W., Wang, L.-L., Huang, W., and Pruski, M.: Enhanced 1H-X D-HMQC performance through improved 1H homonuclear decoupling, Solid State Nucl. Magn. Reson., 98, 12–18, https://doi.org/10.1016/j.ssnmr.2019.01.001, 2019.
Pileio, G., Concistrè, M., McLean, N., Gansmüller, A., Brown, R. C. D., and Levitt, M. H.: Analytical theory of γ-encoded double-quantum recoupling sequences in solid-state nuclear magnetic resonance, J. Magn. Reson., 186, 65–74, https://doi.org/10.1016/j.jmr.2007.01.009, 2007.
Rankin, A. G. M., Trébosc, J., Pourpoint, F., Amoureux, J.-P., and Lafon, O.: Recent developments in MAS DNP-NMR of materials, Solid State Nucl. Magn. Reson., 101, 116–143, https://doi.org/10.1016/j.ssnmr.2019.05.009, 2019.
Rocha, J., Carr, S. W., and Klinowski, J.: 27Al quadrupole nutation and 1H-27Al cross-polarization solid-state NMR studies of ultrastable zeolite Y with fast magic-angle spinning, Chem. Phys. Lett., 187, 401–408, https://doi.org/10.1016/0009-2614(91)80272-Y, 1991.
Tricot, G., Lafon, O., Trébosc, J., Delevoye, L., Méar, F., Montagne, L., and Amoureux, J.-P.: Structural characterisation of phosphate materials: new insights into the spatial proximities between phosphorus and quadrupolar nuclei using the D-HMQC MAS NMR technique, Phys. Chem. Chem. Phys., 13, 16786–16794, https://doi.org/10.1039/C1CP20993K, 2011.
Vega, A. J.: CPMAS of quadrupolar S = nuclei, Solid State Nucl. Magn. Reson., 1, 17–32, https://doi.org/10.1016/0926-2040(92)90006-U, 1992.
Vitzthum, V., Mieville, P., Carnevale, D., Caporini, M. A., Gajan, D., Copéret, C., Lelli, M., Zagdoun, A., Rossini, A. J., Lesage, A., Emsley, L., and Bodenhausen, G.: Dynamic nuclear polarization of quadrupolar nuclei using cross polarization from protons: surface-enhanced aluminium-27 NMR, Chem. Commun., 48, 1988–1990, https://doi.org/10.1039/c2cc15905h, 2012.
Vogt, F. G., Yin, H., Forcino, R. G., and Wu, L.: 17O Solid-State NMR as a Sensitive Probe of Hydrogen Bonding in Crystalline and Amorphous Solid Forms of Diflunisal, Mol. Pharmaceutics, 10, 3433–3446, https://doi.org/10.1021/mp400275w, 2013.
Wittmann, J. J., Mertens, V., Takeda, K., Meier, B. H., and Ernst, M.: Quantification and compensation of the influence of pulse transients on symmetry-based recoupling sequences, J. Magn. Reson., 263, 7–18, https://doi.org/10.1016/j.jmr.2015.12.011, 2016.
Zhao, X., Edén, M., and Levitt, M. H.: Recoupling of heteronuclear dipolar interactions in solid-state NMR using symmetry-based pulse sequences, Chem. Phys. Lett., 342, 353–361, https://doi.org/10.1016/S0009-2614(01)00593-0, 2001.
Zhao, X., Hoffbauer, W., Schmedt auf der Günne, J., and Levitt, M. H.: Heteronuclear polarization transfer by symmetry-based recoupling sequences in solid-state NMR, Solid State Nucl. Magn. Res., 26, 57–64, https://doi.org/10.1016/j.ssnmr.2003.11.001, 2004.