Improved NMR transfer of magnetization from protons to half-integer spin quadrupolar nuclei at moderate and high magic-angle spinning frequencies

Half-integer spin quadrupolar nuclei are the only magnetic isotopes for the majority of the chemical elements. Therefore, the transfer of polarization from protons to these isotopes under magic-angle spinning (MAS) can provide precious insights into the interatomic proximities in hydrogen-containing solids, including organic, hybrid, nanostructured and biological solids. This transfer has recently been combined with dynamic nuclear polarization (DNP) in order to enhance the NMR signal of half-integer quadrupolar isotopes. However, the cross-polarization transfer lacks robustness in the case of quadrupolar nuclei, and we have recently introduced as an alternative technique a D-RINEPT (through-space refocused insensitive nuclei enhancement by polarization transfer) scheme combining a heteronuclear dipolar recoupling built from adiabatic pulses and a continuous-wave decoupling. This technique has been demonstrated at 9.4 T with moderate MAS frequencies, ν_R≈10–15 kHz, in order to transfer the DNP-enhanced ¹H polarization to quadrupolar nuclei. Nevertheless, polarization transfers from protons to quadrupolar nuclei are also required at higher MAS frequencies in order to improve the ¹H resolution. We investigate here how this transfer can be achieved at ν_R≈20 and 60 kHz. We demonstrate that the D-RINEPT sequence using adiabatic pulses still produces efficient and robust transfers but requires large radio-frequency (rf) fields, which may not be compatible with the specifications of most MAS probes. As an alternative, we introduce robust and efficient variants of the D-RINEPT and PRESTO (phase-shifted recoupling effects a smooth transfer of order) sequences using symmetry-based recoupling schemes built from single and composite π pulses. Their performances are compared using the average Hamiltonian theory and experiments at B₀=18.8 T on γ-alumina and isopropylamine-templated microporous aluminophosphate (AlPO₄-14), featuring low and significant ¹H–¹H dipolar interactions, respectively. These experiments demonstrate that the ¹H magnetization can be efficiently transferred to ²⁷Al nuclei using D-RINEPT with $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) recoupling and using PRESTO with $\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) or $\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) schemes at ν_R=20 or 62.5 kHz, respectively. The D-RINEPT and PRESTO recoupling schemes complement each other since the latter is affected by dipolar truncation, whereas the former is not.

We also analyze the losses during these recoupling schemes, and we show how these magnetization transfers can be used at ν_R=62.5 kHz to acquire in 72 min 2D HETCOR (heteronuclear correlation) spectra between ¹H and quadrupolar nuclei, with a non-uniform sampling (NUS).

1 Introduction

Quadrupolar nuclei with a nuclear spin quantum number $S=\mathrm{3}/\mathrm{2}$, $\mathrm{5}/\mathrm{2}$, $\mathrm{7}/\mathrm{2}$ or $\mathrm{9}/\mathrm{2}$ are the only NMR-active isotopes for over 60 % of the chemical elements of the first six periods of the periodic table, including six of the eight most abundant elements by mass in the Earth's crust: O, Al, Ca, Na, Mg and K (Ashbrook and Sneddon, 2014). A wide range of materials, including organic compounds, biological macromolecules, and nanostructured or hybrid materials, contain half-integer spin quadrupolar nuclei and protons. Proximities between these isotopes have notably been probed in solid-state NMR experiments by transferring the polarization of protons to half-integer quadrupolar nuclei through dipolar couplings under magic-angle spinning (MAS) conditions (Rocha et al., 1991; Hwang et al., 2004; Peng et al., 2007; Vogt et al., 2013; Chen et al., 2019). More recently, this polarization transfer has been combined under MAS with dynamic nuclear polarization (DNP) in order to enhance the NMR signals of half-integer spin quadrupolar nuclei (Vitzthum et al., 2012; Perras et al., 2015a; Nagashima et al., 2020). This approach has notably allowed for the detection of insensitive quadrupolar nuclei with low natural abundance, such as ¹⁷O or ⁴³Ca, or low gyromagnetic ratio, γ, such as ^47,49Ti, ⁶⁷Zn or ⁹⁵Mo, near surfaces of materials (Perras et al., 2015a, 2016, 2017; Blanc et al., 2013; Hope et al., 2017; Lee et al., 2017; Nagashima et al., 2020, 2021; Li et al., 2018​​​​​​​).

This transfer has originally been achieved using cross-polarization under MAS (CPMAS) (Harris and Nesbitt, 1988). Nevertheless, this technique lacks robustness for quadrupolar nuclei since the spin-locking of the central transition (CT) between energy levels $\pm \mathrm{1}/\mathrm{2}$ is sensitive to the strength of the quadrupole interaction, the offset, the chemical shift anisotropy (CSA) and the radio-frequency (rf) field inhomogeneity (Vega, 1992; Amoureux and Pruski, 2002; Tricot et al., 2011). Furthermore, CPMAS experiments require a careful adjustment of the rf field applied to the quadrupolar isotope in order to fulfill the Hartmann–Hahn conditions, $(S+\mathrm{1}/\mathrm{2}){\mathit{\nu }}_{\mathrm{1}\mathrm{S}}+\mathit{\epsilon }{\mathit{\nu }}_{\mathrm{1}\mathrm{H}}=n{\mathit{\nu }}_{\mathrm{R}}$, where ν_1S and ν_1H denote the amplitudes of the rf fields applied to the S quadrupolar isotope and to the protons, respectively; $\mathit{\epsilon }=\pm \mathrm{1}$, $n=\pm \mathrm{1}$, or ±2; and ν_R denotes the MAS frequency, while avoiding the rotary resonance recoupling (R³) ${\mathit{\nu }}_{\mathrm{1}\mathrm{S}}=p{\mathit{\nu }}_{\mathrm{R}}/(S+\mathrm{1}/\mathrm{2})$ with p=0, 1, 2 and 3 (Amoureux and Pruski, 2002; Ashbrook and Wimperis, 2009). Moreover, the magnetization of the quadrupolar nuclei cannot be spin-locked for some crystallite orientations, which leads to line-shape distortions (Barrie, 1993; Hayashi and Hayamizu, 1993; Ding and Mcdowell, 1995).

These issues have been circumvented by use of the PRESTO (phase-shifted recoupling effects a smooth transfer of order) scheme (Perras et al., 2015a, b; Zhao et al., 2004) and, more recently, the through-space refocused INEPT (denoted RINEPT hereafter) (Nagashima et al., 2020; Giovine et al., 2019). These schemes benefit from higher robustness than CPMAS since they do not employ a spin-lock on the quadrupolar channel but instead a limited number (two or three) of CT selective pulses. In these sequences, the dipolar interactions between protons and quadrupolar nucleus are reintroduced by applying on the ¹H channel symmetry-based recoupling sequences, such as $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$ for PRESTO or $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ for RINEPT (Zhao et al., 2001; Brinkmann and Kentgens, 2006a). In the case of recoupling sequences built from single square π pulses, the RINEPT sequence using $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ (denoted RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$) is more efficient than PRESTO at ν_R≥60 kHz because of its higher robustness to rf field inhomogeneity and ¹H offset and CSA. At ν_R<20 kHz, the PRESTO technique is more efficient since the efficiency of RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ is reduced by the increased losses due to ¹H–¹H interactions during the $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ recoupling and the windows used to rotor synchronize the $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ blocks, whereas the PRESTO sequence is devoid of these windows (Giovine et al., 2019).

Recently, we have introduced a novel variant of the RINEPT sequence by employing the $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ recoupling built (i) from tanh/tan (tt) adiabatic inversion pulses, (ii) continuous-wave (CW) irradiations during the windows, and (iii) composite $\mathit{\pi }/\mathrm{2}$ and π pulses on the ¹H channel, in order to limit the losses due to ¹H–¹H interactions and improve the transfer efficiency at moderate MAS frequencies (Nagashima et al., 2020, 2021). This novel RINEPT variant, denoted RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\left(\mathrm{tt}\right)$, is more efficient than PRESTO and CPMAS at ν_R≈12.5 kHz, and it has been combined with DNP to detect the NMR signals of quadrupolar nuclei with small dipolar coupling with protons, including the low-γ isotopes, such as ^47,49Ti, ⁶⁷Zn or ⁹⁵Mo, and unprotonated ¹⁷O nuclei. Furthermore, for quadrupolar nuclei subject to large dipolar interactions, such as ¹⁷O nuclei of OH groups, we have shown that a RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\left(\mathrm{tt}\right)$ version with only two pulses on the quadrupolar channel is more efficient that its PRESTO counterpart (Nagashima et al., 2021).

However, several NMR experiments require the transfer of ¹H magnetization to quadrupolar nuclei at ν_R>12.5 kHz. In particular, MAS frequencies of ν_R≥20 kHz are needed to avoid the overlap between the center bands and the spinning sidebands of satellite transitions (STs) in ²⁷Al NMR spectra at 18.8 T. In addition, magnetization transfers at ν_R≥60 kHz are advantageous to acquire through-space heteronuclear correlation (D-HETCOR) 2D spectra between protons and quadrupolar nuclei endowed with high resolution along the ¹H dimension since fast MAS averages out the ¹H–¹H dipolar couplings.

Concurrently, we have demonstrated that the efficiency of PRESTO transfers using the $\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$ recoupling can be improved at ν_R=62.5 kHz using (270₀90₁₈₀) composite π pulses as a basic inversion element, where the standard notation for the pulses is used: ξ_ϕ denotes a rectangular, resonant rf pulse with flip angle ξ and phase ϕ in degrees (Giovine et al., 2019). More recently, $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ and $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$ recoupling schemes built from (90₋₄₅90₄₅90₋₄₅) composite π pulses have been proposed, but they have not yet been incorporated into RINEPT transfers (Perras et al., 2019). Globally, no systematic study of the $\mathrm{R}{N}_n^{\mathit{\nu }}$​​​​​​​ recouplings built from composite π pulses has been carried out.

In the present article, we investigate the use of RINEPT-CWc using an adiabatic recoupling scheme at the higher MAS frequencies of ν_R=20 and 62.5 kHz. We demonstrate using numerical simulations of spin dynamics and experiments on γ-alumina and isopropylamine-templated microporous aluminophosphate (AlPO₄-14) (hereafter AlPO₄-14) that the rf requirement of this technique increases with the ¹H–¹H dipolar interactions. In practice, this rf requirement is not compatible with the specifications of most MAS probes at ν_R≥20 kHz, even for moderate ¹H–¹H dipolar interactions. As an alternative, we introduce variants of the PRESTO and RINEPT sequences by selecting with average Hamiltonian (AH) theory recoupling schemes built from single rectangular or composite π pulses. Finally, using experiments on γ-alumina and AlPO₄-14, which feature small and moderate ¹H–¹H dipolar interactions, respectively, we identify the most robust and efficient PRESTO and RINEPT transfers at B₀=18.8 T with ν_R=20 and 62.5 kHz.

2 Pulse sequences and theory

2.1 PRESTO

2.1.1 Single-quantum heteronuclear dipolar recoupling

A $\mathrm{R}{N}_n^{\mathit{\nu }}$ sequence, where N is an even positive integer and n and ν are integers, consists of $N/\mathrm{2}$ pairs of elements ${\mathcal{R}}_{\mathit{\varphi }}{\mathcal{R}}_{-\mathit{\varphi }}^{\prime }$​​​​​​​, with $\mathit{\varphi }=\mathit{\pi }\mathit{\nu }/N$ radians an overall phase shift. ℛ_ϕ is an inversion pulse with a duration of $n{T}_{\mathrm{R}}/N$, where $T_{\mathrm{R}}=\mathrm{1}/{\mathit{\nu }}_{\mathrm{R}}$ is the rotor period, and ${\mathcal{R}}_{-\mathit{\varphi }}^{\prime }$ is an inversion pulse derived from ℛ by changing the sign of all phases. ℛ and ℛ^′ are identical when they are amplitude modulated; i.e., all phase shifts are multiples of π. The rf field requirement of $\mathrm{R}{N}_n^{\mathit{\nu }}$ is equal to

$$\begin{array}{}\text{(1)}& {\mathit{\nu }}_{\mathrm{1}}={\displaystyle \frac{N}{n}}{\displaystyle \frac{{\mathit{\xi }}^{\mathrm{tot}}}{\mathrm{2}\mathit{\pi }}}{\mathit{\nu }}_{\mathrm{R}},\end{array}$$

where ${\mathit{\xi }}^{\mathrm{tot}}=\sum _{i=\mathrm{1}}^P{\mathit{\xi }}^i$ is the sum of the flip angles of the P individual pulses of the ℛ element.

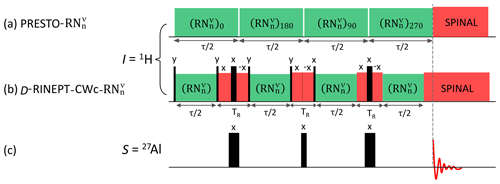
Figure 1 The ¹H → ²⁷Al (a, c) PRESTO-$\mathrm{R}{N}_n^{\mathit{\nu }}$ and (b, c) D-RINEPT-CWc-$\mathrm{R}{N}_n^{\mathit{\nu }}$ pulse sequences. Those applied to the ¹H channel are displayed in panels (a) and (b), whereas that applied to the ²⁷Al channel is shown in panel (c). The narrow and broad black bars represent $\mathit{\pi }/\mathrm{2}$ and π pulses, respectively. The acquisition of the free-induction decays (FIDs) (indicated with the vertical dashed line) starts after (a) the end of the $\mathrm{R}{N}_n^{\mathit{\nu }}$ block in the case of PRESTO or (b) on top of the echo shifted with $T_{\mathrm{R}}/\mathrm{2}$ with respect to the end of the last recoupling block in the case of RINEPT.

In the PRESTO sequence (Fig. 1a), symmetry-based γ-encoded $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes applied to the ¹H channel reintroduce the |m|=2 space components and the single-quantum (SQ) terms of the heteronuclear dipolar couplings between the protons and the quadrupolar nuclei, as well as the ¹H CSA, while they suppress the contributions of ¹H isotropic chemical shifts, the heteronuclear J couplings with protons, and the ¹H–¹H dipolar couplings to the first-order AH (Zhao et al., 2004). The heteronuclear dipolar interaction is characterized by a space rank l and a spin rank λ. A γ-encoded |m|=2 SQ heteronuclear dipolar recoupling must selectively reintroduce the two components $\mathit{\{}l,m,\mathit{\lambda },\mathit{\mu }\mathit{\}}=\mathit{\{}\mathrm{2},\mathrm{2},\mathrm{1},\mathit{\mu }\mathit{\}}$ and $\mathit{\{}\mathrm{2},-\mathrm{2},\mathrm{1},-\mathit{\mu }\mathit{\}}$ of the heteronuclear dipolar coupling and ¹H CSA with $\mathit{\mu }=\pm \mathrm{1}$, while all other components must be suppressed.

During these recoupling schemes, the contribution of the dipolar coupling between I=¹H and S nuclei to the first-order Hamiltonian is equal to (Zhao et al., 2004)

$$\begin{array}{}\text{(2)}& {\stackrel{\mathrm{‾}}{H}}_{D,IS}^{\left(\mathrm{1}\right)}={\mathit{\omega }}_{D,IS}{S}_z\left[I^{+}\exp \left(i\mathrm{2}\mathit{\phi }\right)+I^{-}\exp \left(-i\mathrm{2}\mathit{\phi }\right)\right],\end{array}$$

where $I^{\pm }=I_x\pm i{I}_y$ symbols represent the shift operators, and the magnitude and phase of the recoupled I–S dipolar coupling are given by

$$\begin{array}{}\text{(3)}& {\mathit{\omega }}_{D,IS}=-\mathit{\kappa }{\displaystyle \frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{b}_{IS}{\sin }^{\mathrm{2}}\left({\mathit{\beta }}_{PR}^{D,IS}\right)\end{array}$$

and

$$\begin{array}{}\text{(4)}& \mathit{\phi }={\mathit{\gamma }}_{PR}^{D,IS}-{\mathit{\omega }}_{\mathrm{R}}{t}^{\mathrm{0}},\end{array}$$

respectively, where b_IS is the dipolar coupling constant in rad/s, and κ is the scaling factor of the recoupled heteronuclear dipolar interaction, which depends on the $\mathrm{R}{N}_n^{\mathit{\nu }}$ symmetry and the ℛ element. The Euler angles $\left\{\mathrm{0},{\mathit{\beta }}_{PR}^{D,IS},{\mathit{\gamma }}_{PR}^{D,IS}\right\}$ relate the I–S​​​​​​​ vector to the MAS rotor frame, and t⁰ refers to the starting time of the recoupling. The norm of ${\stackrel{\mathrm{‾}}{H}}_{D,IS}^{\left(\mathrm{1}\right)}$ does not depend on the ${\mathit{\gamma }}_{PR}^{D,IS}$ angle, since these recoupling schemes are γ encoded (Pileio et al., 2007; Martineau et al., 2012). The Hamiltonian of Eq. (2) does not commute among different spin pairs; hence, the PRESTO sequence is affected by dipolar truncation; i.e., the transfer to distant nuclei is attenuated by the stronger couplings with nearby spins (Bayro et al., 2009).

As mentioned above, the SQ heteronuclear dipolar recoupling schemes also reintroduce the ¹H CSA with the same scaling factor κ but without commuting with the recoupled ¹H–S dipolar interactions. Therefore, in the case of large ¹H CSA, for instance at high magnetic fields, this interaction can interfere with the ¹H–S dipolar couplings, especially with the small ones. These interferences can be limited by the use of the PRESTO-III variant, depicted in Fig. 1a, c (Zhao et al., 2004), in which three CT-selective pulses are applied to the S channel. Indeed, the CT-selective π pulses partly refocus the ¹H CSA, which limits these interferences.

2.1.2 Selection of the recoupling sequence

On the basis of the AH and spin dynamics simulations, the $\mathrm{R}{\mathrm{18}}_{\mathrm{1}}^{\mathrm{7}}$ and $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$ schemes built from single rectangular π pulses were selected for heteronuclear dipolar recoupling at moderate MAS frequencies, ν_R ≈10 kHz (Zhao et al., 2001), while, more recently, sequences based on symmetries $\mathrm{R}{\mathrm{12}}_{\mathrm{5}}^{\mathrm{4}}$, $\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$, $\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$, $\mathrm{R}{\mathrm{14}}_{\mathrm{8}}^{\mathrm{5}}$, $\mathrm{R}{\mathrm{18}}_{\mathrm{8}}^{\mathrm{7}}$, $\mathrm{R}{\mathrm{16}}_{\mathrm{9}}^{\mathrm{6}}$, $\mathrm{R}{\mathrm{20}}_{\mathrm{9}}^{\mathrm{8}}$ and $\mathrm{R}{\mathrm{18}}_{\mathrm{10}}^{\mathrm{7}}$ using (270₀90₁₈₀) as inversion element were chosen for the measurement of ¹H CSA at fast MAS frequencies, ν_R≈60–70 kHz (Pandey et al., 2015). We also transferred the proton polarization to ²⁷Al nuclei at ν_R=62.5 kHz using PRESTO with $\mathrm{R}{\mathrm{16}}_{\mathrm{3}}^{\mathrm{2}}$ recoupling built from a single rectangular π pulse (Giovine et al., 2019).

We screened here the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes built from single rectangular and composite π pulses to achieve γ-encoded |m|=2 heteronuclear SQ dipolar recoupling at ν_R=20 or 62.5 kHz. Dipolar recoupling at ν_R≥60 kHz is useful to correlate the signals of quadrupolar nuclei with high-resolution ¹H spectra without using homonuclear dipolar decoupling. We tested the three following composite π pulses: (1) (270₀90₁₈₀), which is offset compensated and amplitude modulated and has been employed in several $\mathrm{R}{N}_n^{\mathit{\nu }}$ sequences (Giovine et al., 2019; Carravetta et al., 2000; Levitt, 2002; Pandey et al., 2015); (2) (90₀240₉₀90₀), which compensates both rf inhomogeneity and offset (Freeman et al., 1980; Duong et al., 2019); and (3) (90₋₄₅90₄₅90₋₄₅), which has homonuclear decoupling properties (Madhu et al., 2001). Adiabatic pulses cannot be employed for SQ heteronuclear dipolar recoupling since they yield vanishing scaling factors for the rotational components with μ≠0 (Nagashima et al., 2018).

A total of 109 $\mathrm{R}{N}_n^{\mathit{\nu }}$ symmetries with $\mathrm{2}\le N\le \mathrm{30}$, $\mathrm{2}\le n\le \mathrm{7}$ and $\mathrm{1}\le \mathit{\nu }\le \mathrm{11}$ were found which recouple the $\mathit{\{}\mathrm{2},\pm \mathrm{2},\mathrm{1},\pm \mathrm{1}\mathit{\}}$ or $\mathit{\{}\mathrm{2},\mp \mathrm{2},\mathrm{1},\pm \mathrm{1}\mathit{\}}$ rotational components of the ¹H–S dipolar coupling and ¹H CSA. We selected the $\mathrm{R}{N}_n^{\mathit{\nu }}$ recouplings based on those symmetries with rf field limited to ν₁≤120 and 190 kHz for ν_R=20 and 62.5 kHz, respectively. We only considered the $\mathrm{R}{N}_n^{\mathit{\nu }}$ symmetries with $\mathrm{45}\le \mathit{\varphi }\le \mathrm{135}$^∘ since sequences with ϕ close to 90^∘ are better compensated for rf field errors and inhomogeneities (Brinkmann and Kentgens, 2006b). The scaling factor, κ, of the recoupled ¹H–S dipolar interaction was calculated using the “C and R symmetries” Mathematica package (Carravetta et al., 2000; Brinkmann and Levitt, 2001; Brinkmann et al., 2000; Brinkmann and Edén, 2004).

These $\mathrm{R}{N}_n^{\mathit{\nu }}$ symmetries eliminate the contribution of ¹H–¹H dipolar interactions to the first-order Hamiltonian but not their contribution to the second order. The cross terms between ¹H–¹H interactions in the second-order Hamiltonian can be written (Brinkmann and Edén, 2004):

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\stackrel{\mathrm{‾}}{H}}^{\left(\mathrm{2}\right),{\mathrm{DD}}_{\mathrm{1}}\times {\mathrm{DD}}_{\mathrm{2}}}& ={\displaystyle \frac{\mathrm{1}}{{\mathit{\nu }}_{\mathrm{R}}}}\sum _{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{{\mathrm{DD}}_{\mathrm{1}}\times {\mathrm{DD}}_{\mathrm{2}}}{\left[A_{l_{\mathrm{2}}{m}_{\mathrm{2}}}^{{\mathrm{DD}}_{\mathrm{2}}}\right]}^R{\left[A_{l_{\mathrm{1}}{m}_{\mathrm{1}}}^{{\mathrm{DD}}_{\mathrm{1}}}\right]}^R\\ & \times \exp \left[i\left(m_{\mathrm{1}}+m_{\mathrm{2}}\right){\mathit{\omega }}_{\mathrm{R}}{t}^{\mathrm{0}}\right]\left[T_{{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\mu }}_{\mathrm{2}}}^{{\mathrm{DD}}_{\mathrm{2}}},T_{{\mathit{\lambda }}_{\mathrm{1}}{\mathit{\mu }}_{\mathrm{1}}}^{{\mathrm{DD}}_{\mathrm{1}}}\right],\end{array}\end{array}$$

where the sum is taken over all second-order cross terms {1,2} between the $\mathit{\{}{l}_{\mathrm{1}},m_{\mathrm{1}},{\mathit{\lambda }}_{\mathrm{1}},{\mathit{\mu }}_{\mathrm{1}}\mathit{\}}$ and $\mathit{\{}{l}_{\mathrm{2}},m_{\mathrm{2}},{\mathit{\lambda }}_{\mathrm{2}},{\mathit{\mu }}_{\mathrm{2}}\mathit{\}}$ rotational components of DD₁ and DD₂ ¹H–¹H dipolar interactions, respectively. ${\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{{\mathrm{DD}}_{\mathrm{1}}\times {\mathrm{DD}}_{\mathrm{2}}}$ is the scaling factor of this cross term; ${\left[A_{l_i{m}_i}^{{\mathrm{DD}}_i}\right]}^R$ and $T_{{\mathit{\lambda }}_i{\mathit{\mu }}_i}^{{\mathrm{DD}}_i}$ denote the component m_i of the l_ith rank spatial irreducible spherical tensor $A^{{\mathrm{DD}}_i}$ in the MAS rotor-fixed frame and the component μ_i of the λ_ith rank spin irreducible spherical tensor operator $T^{{\mathrm{DD}}_i}$. Equation (5) indicates that the amplitude of the second-order Hamiltonian decreases at higher MAS frequencies. The magnitude of the cross terms between ¹H–¹H interactions was estimated by calculating the Euclidean norm (Hu et al., 2009; Gansmüller et al., 2013):

$$\begin{array}{}\text{(6)}& {∥{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{{\mathrm{DD}}_{\mathrm{1}}\times {\mathrm{DD}}_{\mathrm{2}}}∥}_{\mathrm{2}}=\sqrt{\sum _{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}{\left|{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{{\mathrm{DD}}_{\mathrm{1}}\times {\mathrm{DD}}_{\mathrm{2}}}\right|}^{\mathrm{2}}}.\end{array}$$

For each basic element ℛ, we selected the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes with the highest ratio $\mathit{\kappa }/{∥{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{{\mathrm{DD}}_{\mathrm{1}}\times {\mathrm{DD}}_{\mathrm{2}}}∥}_{\mathrm{2}}$ in order to minimize the interference of ¹H–¹H dipolar interactions with the ¹H–S dipolar recoupling. Besides ¹H–¹H dipolar interactions, other cross terms involving ¹H CSA and offset can also interfere with the ¹H–S dipolar recoupling. These cross terms can be expressed by Eq. (5), in which DD₁ and DD₂ indexes are substituted by other interactions, such as ¹H CSA or isotropic chemical shift (δ_iso). For the selected symmetries, we estimated the magnitude of the cross terms between ¹H CSA or offset by calculating the Euclidean norms ${∥{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{\mathrm{CSA}\times \mathrm{CSA}}∥}_{\mathrm{2}}$ and ${∥{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{\mathit{\delta }\mathrm{iso}\times \mathit{\delta }\mathrm{iso}}∥}_{\mathrm{2}}$ given by Eq. (6).

The corresponding selected $\mathrm{R}{N}_n^{\mathit{\nu }}$ sequences are listed in Tables S1 and S2 in the Supplement for ν_R=20 and 62.5 kHz, respectively.

For ν_R=20 kHz, according to the AH, the $\mathrm{R}{N}_n^{\mathit{\nu }}$ sequence with the highest robustness to ¹H–¹H dipolar interactions is $\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}({\mathrm{180}}_{\mathrm{0}}$). However, this recoupling is slightly less robust to ¹H CSA and offset than $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}({\mathrm{180}}_{\mathrm{0}}$), which has already been reported. For this MAS frequency, the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes using the chosen composite pulses either required rf fields greater than 120 kHz, e.g., ν₁=130 and 173 kHz for the R26${}_{\mathrm{3}}^{\mathrm{7}}$ schemes built from (90₋₄₅90₄₅90₋₄₅) and (270₀90₁₈₀) pulses, or did not suppress efficiently the second-order cross terms between ¹H–¹H interactions because of small rf field (ν₁≤62.5 kHz).

For ν_R=62.5 kHz, the $\mathrm{R}{N}_n^{\mathit{\nu }}$ sequences using composite π pulses recouple the ¹H–S dipolar interaction with a higher scaling factor than those built from single π pulses. According to AH, the (90₀240₉₀90₀) basic element leads to the highest robustness to ¹H–¹H interferences. Even if the amplitude of the cross terms is inversely proportional to the MAS frequency (Eq. 5), the amplitude of these terms is lower at ν_R=20 than 62.5 kHz. The (270₀90₁₈₀) element is less robust to ¹H–¹H interferences but benefits from a high robustness to offset. The selected $\mathrm{R}{N}_n^{\mathit{\nu }}$ symmetries for this element include $\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$ and $\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$, which have already been employed for the measurement of ¹H CSA and the transfer of ¹H polarization to half-integer quadrupolar nuclei at ν_R≥60 kHz (Giovine et al., 2019; Pandey et al., 2015). The scaling factors κ of the ¹H–S dipolar interaction of the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes built from single π pulses are small with $\mathrm{45}\le \mathit{\varphi }\le \mathrm{135}$^∘; hence, we also selected in Table S3 those with an extended ϕ range of 20–160^∘. These recoupling schemes are less robust to offset than the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes built from (270₀90₁₈₀) element.

2.2 D-RINEPT

2.2.1 Zero-quantum heteronuclear dipolar recoupling

In the D-RINEPT sequence, the ¹H–S dipolar interactions are reintroduced under MAS by applying non-γ-encoded two-spin order dipolar recoupling to the ¹H channel. These schemes reintroduce the |m|=2 space components and the zero-quantum (0Q) terms of the ¹H–S dipolar interaction and ¹H CSA; i.e., the rotational components $\mathit{\{}l,m,\mathit{\lambda },\mathit{\mu }\mathit{\}}=\mathit{\{}\mathrm{2},\pm \mathrm{2},\mathrm{1},\mathrm{0}\mathit{\}}$, while they suppress the contributions of ¹H isotropic chemical shifts, the heteronuclear J couplings with protons, and the ¹H–¹H dipolar couplings to the first-order AH (Brinkmann and Kentgens, 2006a, b). The contribution of the ¹H–S dipolar coupling to this Hamiltonian is equal to (Giovine et al., 2019; Brinkmann and Kentgens, 2006a; Lu et al., 2012)

$$\begin{array}{}\text{(7)}& {\stackrel{\mathrm{‾}}{H}}_{D,IS}^{\left(\mathrm{1}\right)}=\mathrm{2}{\mathit{\omega }}_{D,IS}{I}_z{S}_z,\end{array}$$

where

$$\begin{array}{}\text{(8)}& {\mathit{\omega }}_{D,IS}=\mathit{\kappa }{b}_{IS}{\sin }^{\mathrm{2}}\left({\mathit{\beta }}_{PR}^{D,IS}\right)\cos \left(\mathrm{2}\mathit{\phi }\right).\end{array}$$

The norm of ${\stackrel{\mathrm{‾}}{H}}_{D,IS}^{\left(\mathrm{1}\right)}$ depends on the φ phase, given by Eq. (4), and hence on the ${\mathit{\gamma }}_{PR}^{D,IS}$ angle. Therefore, these two-spin order dipolar recoupling schemes are non-γ-encoded. The Hamiltonian of Eq. (7) commutes among different spin pairs; hence, these recoupling schemes are not affected by dipolar truncation. Similarly, the recoupled ¹H CSA contribution to the first-order Hamiltonian is proportional to I_z and hence also commutes with the recoupled ¹H–S dipolar interactions and does not interfere with the heteronuclear dipolar recoupling.

2.2.2 Selection of the recoupling sequence

Different $\mathrm{R}{N}_n^{\mathit{\nu }}$ sequences have been proposed to achieve non-γ-encoded |m|=2 two-spin order dipolar recoupling, including (i) symmetries $\mathrm{R}(\mathrm{4}n{)}_n^{\mathrm{2}n-\mathrm{1}}=\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$, $\mathrm{R}{\mathrm{16}}_{\mathrm{4}}^{\mathrm{7}}$, $\mathrm{R}{\mathrm{20}}_{\mathrm{5}}^{\mathrm{9}}$, $\mathrm{R}{\mathrm{24}}_{\mathrm{6}}^{\mathrm{11}}$, $\mathrm{R}{\mathrm{28}}_{\mathrm{7}}^{\mathrm{13}}$ and $\mathrm{R}{\mathrm{32}}_{\mathrm{8}}^{\mathrm{15}}$ for n=3, 4, 5, 6, 7 and 8 using single π pulses as basic element, which have been employed to measure ¹H–¹⁷O dipolar couplings at ν_R=50 kHz (Brinkmann and Kentgens, 2006b); (ii) $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ recoupling built from a single π pulse, which corresponds to the ${\left[\mathrm{R}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\mathrm{R}{\mathrm{4}}_{\mathrm{1}}^{-\mathrm{2}}\right]}_{\mathrm{0}}{\left[\mathrm{R}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\mathrm{R}{\mathrm{4}}_{\mathrm{1}}^{-\mathrm{2}}\right]}_{\mathrm{120}}{\left[\mathrm{R}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\mathrm{R}{\mathrm{4}}_{\mathrm{1}}^{-\mathrm{2}}\right]}_{\mathrm{240}}$ sequence and has been employed in the RINEPT scheme (Nagashima et al., 2021; Giovine et al., 2019); (iii) $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$ and $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ schemes using a (90₋₄₅90₄₅90₋₄₅) composite π pulse as a basic element, which have been incorporated into D-HMQC (heteronuclear multiple quantum coherence) at ν_R=36 kHz (Perras et al., 2019), and (iv) $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ schemes built from a (tt) adiabatic pulse, which have been used in the RINEPT sequence (Nagashima et al., 2021, 2020). During the (tt) pulse, the instantaneous rf amplitude is equal to

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& {\mathit{\omega }}_{\mathrm{1}}\left(t\right)=\\ & {\mathit{\omega }}_{\mathrm{1},max}\left\{\begin{array}{ll}\tanh \left[\frac{\mathrm{8}\mathit{\xi }t}{T_{\mathrm{R}}}\right]& \mathrm{0}\le t<T_{\mathrm{R}}/\mathrm{8},\\ \tanh \left[\mathrm{2}\mathit{\xi }\left(\mathrm{1}-\frac{\mathrm{4}t}{T_{\mathrm{R}}}\right)\right]& T_{\mathrm{R}}/\mathrm{8}\le t<T_{\mathrm{R}}/\mathrm{4},\end{array}\right.\end{array}\end{array}$$

where ${\mathit{\omega }}_{\mathrm{1},max}$ is the peak amplitude of the rf field, t refers to the time since the start of the pulse, which lasts $T_{\mathrm{R}}/\mathrm{4}$ when incorporated into the $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ recoupling scheme. The parameter ξ determines the rise and fall times of the pulse. Hence, in the frequency-modulated (FM) frame (Garwood and DelaBarre, 2001), the frequency offset is

$$\begin{array}{}\text{(10)}& {\mathit{\varphi }}_I\left(t\right)={\displaystyle \frac{\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}}{\mathrm{2}\mathit{\theta }\tan \left(\mathit{\theta }\right)}}\ln \left\{\cos \left[\mathit{\theta }\left(\mathrm{1}-\mathrm{8}{\displaystyle \frac{t}{T_{\mathrm{R}}}}\right)\right]\right\},\end{array}$$

where $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}$ is the peak amplitude of the carrier frequency modulation, and θ determines the frequency sweep rate in the center of the pulse. Here, we employed ξ=10 and $\mathit{\theta }=\mathrm{87}{}^{\circ }=\mathrm{atan}\left(\mathrm{20}\right)$ (Kervern et al., 2007; Nagashima et al., 2018, 2020).

We screened here the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes built from (180₀), (270₀90₁₈₀), (90₀240₉₀90₀) and (90₋₄₅90₄₅90₋₄₅) inversion elements. A total of 58 $\mathrm{R}{N}_n^{\mathit{\nu }}$ symmetries with $\mathrm{2}\le N\le \mathrm{30}$, $\mathrm{2}\le n\le \mathrm{7}$ and $\mathrm{1}\le \mathit{\nu }\le \mathrm{11}$ were found which recouple the $\mathit{\{}\mathrm{2},\pm \mathrm{2},\mathrm{1},\mathrm{0}\mathit{\}}$ rotational components of the ¹H–S dipolar coupling and ¹H CSA. We only considered the $\mathrm{R}{N}_n^{\mathit{\nu }}$ symmetries with $\mathrm{60}\le \mathit{\varphi }\le \mathrm{120}$^∘ since the currently employed non-γ-encoded |m|=2 two-spin order heteronuclear dipolar recoupling schemes have $\mathrm{75}\le \mathit{\varphi }\le \mathrm{90}$^∘.

We calculated the scaling factor of the recoupled ¹H–S dipolar interaction and the Euclidean norm ${∥{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{{\mathrm{DD}}_{\mathrm{1}}\times {\mathrm{DD}}_{\mathrm{2}}}∥}_{\mathrm{2}}$ of the cross terms between ¹H–¹H interactions using the “C and R symmetries” Mathematica package. For each basic element ℛ, we selected the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes with the highest ratios $\mathit{\kappa }/{∥{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{{\mathrm{DD}}_{\mathrm{1}}\times {\mathrm{DD}}_{\mathrm{2}}}∥}_{\mathrm{2}}$. The selected $\mathrm{R}{N}_n^{\mathit{\nu }}$ sequences are listed in Table S4, along with the parameters of the $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ schemes built from the different basic elements ℛ for the sake comparison. For these sequences, we calculated the Euclidean norms, ${∥{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{\mathrm{CSA}\times \mathrm{CSA}}∥}_{\mathrm{2}}$ and ${∥{\mathit{\kappa }}_{\mathit{\{}\mathrm{1},\mathrm{2}\mathit{\}}}^{\mathit{\delta }\mathrm{iso}\times \mathit{\delta }\mathrm{iso}}∥}_{\mathrm{2}}$, in order to estimate the magnitudes of the cross terms between ¹H CSA and offset.

According to the AH, the (90₀240₉₀90₀) composite π pulse yields the highest robustness to ¹H–¹H dipolar interactions. However, the rf field requirement of the $\mathrm{R}{N}_n^{\mathit{\nu }}$ sequences built from this composite pulse, ${\mathit{\nu }}_{\mathrm{1}}=\mathrm{1.16}N{\mathit{\nu }}_{\mathrm{R}}/n$, is not compatible at ν_R=62.5 kHz with most 1.3 mm MAS probes (e.g., ν₁=291 kHz for $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$). Furthermore, the highest robustness to ¹H CSA and offset are achieved using the (270₀90₁₈₀) composite π pulse. The $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ schemes benefit from the highest robustness to ¹H CSA because of the three-step multiple-quantum super-cycle (Brinkmann and Edén, 2004; Brinkmann and Kentgens, 2006a). Contrary to the $\mathrm{R}{N}_n^{\mathit{\nu }}$ with |m|=2 SQ heteronuclear dipolar recouplings, the rf field of the $\mathrm{R}{N}_n^{\mathit{\nu }}$ with |m|=2 two-spin order schemes is always higher than 2ν_R since these symmetries with 2n>N, such as $\mathrm{R}{\mathrm{12}}_{\mathrm{9}}^{\mathrm{5}}$, have smaller κ scaling factors for the basic elements employed here.

In the case of the adiabatic $\mathrm{R}{N}_n^{\mathit{\nu }}$ (tt) sequences, the determination of the scaling factors of the first- and second-order terms of the effective Hamiltonian is more cumbersome since they depend on the ${\mathit{\nu }}_{\mathrm{1},max}$, $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}$, ξ and θ parameters (Nagashima et al., 2018). For example, the scaling factor of the $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$ and $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ schemes is κ=0.31 for ${\mathit{\nu }}_{\mathrm{1},max}/\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}=\mathrm{0.685}$, ξ=10 and θ=87^∘, and this value monotonously decreases for increasing ${\mathit{\nu }}_{\mathrm{1},max}/\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}$ ratios.

2.2.3 D-RINEPT-CWc sequence

The D-RINEPT-CWc sequence is displayed in Fig. 1b and c. The ¹H–S dipolar couplings are reintroduced by applying the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes listed in Table S4 during the defocusing and refocusing delays τ, which are identical in this article, even if distinct delays can improve the transfer efficiency (Nagashima et al., 2021). As the two-spin order recoupling schemes are non-γ-encoded, they must be rotor synchronized. We used here a delay of T_R between two successive $\mathrm{R}{N}_n^{\mathit{\nu }}$ blocks. In the D-RINEPT-CWc sequence, a CW irradiation is applied during these delays in order to limit the losses due to ¹H–¹H dipolar interactions (Nagashima et al., 2021). The nutation during this CW irradiation is eliminated by employing CW irradiations with opposite phases. Furthermore, the robustness to ¹H rf field inhomogeneity is improved by replacing the first π and second $\mathit{\pi }/\mathrm{2}$ pulses by composite (90₀180₉₀90₀) and (90₉₀90₀) pulses, respectively, with the CW irradiation being applied between the individual pulses (Freeman et al., 1980; Levitt and Freeman, 1979).

3 Numerical simulations

3.1 Simulation parameters

All simulations were performed using version 4.1.1 of the SIMPSON package (Bak et al., 2000). The powder average was performed using 462 $\mathit{\{}{\mathit{\alpha }}_{\mathrm{MR}},{\mathit{\beta }}_{\mathrm{MR}},{\mathit{\gamma }}_{\mathrm{MR}}\mathit{\}}$ Euler angles relating the molecular and rotor frames. This set of angles was obtained by considering 66 {α_MR,β_MR} pairs and 7 γ_MR angles. The {α_MR,β_MR} values were selected according to the REPULSION algorithm (Bak and Nielsen, 1997), while the γ_MR angles were regularly stepped from 0 to 360^∘.

To accelerate the simulations, we used a ¹H → ¹⁵N RINEPT transfer instead of the ¹H → ²⁷Al one, because the computing time is proportional to the cube of the size of the density matrix. Furthermore, in RINEPT experiments, only CT-selective pulses are applied to the quadrupolar nuclei; hence, the contribution of the STs to the signal can be disregarded. The ¹H → ¹⁵N RINEPT transfer was simulated for a ¹⁵N¹H₄ spin system. A similar approach has already been applied for the simulation of the RINEPT transfer from protons to quadrupolar nuclei (Nagashima et al., 2021; Giovine et al., 2019). This ¹⁵N¹H₄ spin system comprises a tetrahedron of four protons with a ¹⁵N nucleus on one of its symmetry axes. The dipolar coupling constants between protons are all equal to $\left|b_{\mathrm{HH}}\right|/\left(\mathrm{2}\mathit{\pi }\right)=\mathrm{1}$, 7 or 15 kHz. The dipolar coupling between the ¹⁵N nucleus and its closest ¹H neighbor is $\left|b_{\mathrm{HN}}\right|/\left(\mathrm{2}\mathit{\pi }\right)=\mathrm{2575}$ Hz, corresponding to a ¹H–²⁷Al distance of 2.3 Å, typical of the distance between the protons of hydroxyl groups and the Al atoms of the first surface layer of hydrated γ-alumina (Lee et al., 2014). All protons were subject to a CSA of 6 kHz, i.e., 7.5 ppm at 18.8 T, with a null asymmetry parameter (Liang et al., 2018). We simulated the ¹H → ¹⁵N RINEPT-CWc sequences by incorporating either $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) or $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) recoupling schemes. We used a static magnetic field of 18.8 T, for which the ¹H and ¹⁵N Larmor frequencies were equal to 800 and 81 MHz, respectively, and MAS frequencies of ν_R=20 or 62.5 kHz. The defocusing and refocusing periods were both equal to their optimal values τ=650 or 640 µs at ν_R=20 or 62.5 kHz, respectively. The rf field nutation frequency on the ¹H channel was equal to 200 kHz during the $\mathit{\pi }/\mathrm{2}$ and π pulses that do not belong to the recoupling sequence, as well as the CW irradiation, whereas the pulses applied to S =¹⁵N nuclei were considered ideal Dirac pulses. For the (tt) adiabatic pulses, the simulations were performed with ${\mathit{\nu }}_{\mathrm{1},max}/{\mathit{\nu }}_{\mathrm{R}}$ and $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}/{\mathit{\nu }}_{\mathrm{R}}$ ratios ranging from 0.5 to 10 and from 10 to 200, respectively. All other pulses were applied on resonance. The density matrix before the first pulse was equal to $I_{\mathrm{1}z}+I_{\mathrm{2}z}+I_{\mathrm{3}z}+I_{\mathrm{4}z}$. We normalized the transfer efficiency of the ¹H → ¹⁵N RINEPT sequences to the maximal signal for a ¹H → ¹⁵N through-bond RINEPT sequence made of ideal Dirac pulses in the case of a ¹⁵N–¹H spin system with a J-coupling constant of 150 Hz.

3.2 Optimal adiabatic recoupling

The transfer efficiency of RINEPT using $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes built from adiabatic (tt) pulses depends on ${\mathit{\nu }}_{\mathrm{1},max}$ and $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}$ parameters. For a similar ¹⁵N¹H₄ spin system with $\left|b_{\mathrm{HN}}\right|/\left(\mathrm{2}\mathit{\pi }\right)=\mathrm{2.575}$ and $\left|b_{\mathrm{HH}}\right|/\left(\mathrm{2}\mathit{\pi }\right)=\mathrm{7}$ kHz, spinning at ν_R=12.5 kHz, we showed using numerical simulations that a maximal transfer efficiency was achieved provided that ${\mathit{\nu }}_{\mathrm{1},max}=\mathrm{0.07}\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}$ and ${\mathit{\nu }}_{\mathrm{1},max}/{\mathit{\nu }}_{\mathrm{R}}\ge \mathrm{8}$ (Nagashima et al., 2021). In practice, we used ${\mathit{\nu }}_{\mathrm{1},max}=\mathrm{11}{\mathit{\nu }}_{\mathrm{R}}=\mathrm{137}$ kHz and $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}=\mathrm{160}{\mathit{\nu }}_{\mathrm{R}}=\mathrm{2}$ MHz.

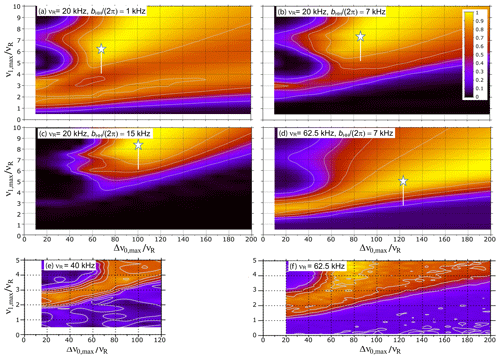
Figure 2 (a–d) Simulated transfer efficiency of ¹H → ¹⁵N D-RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\left(\mathrm{tt}\right)$ sequence for a ¹⁵N¹H₄ spin system as a function of ${\mathit{\nu }}_{\mathrm{1},max}/{\mathit{\nu }}_{\mathrm{R}}$ and $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}/{\mathit{\nu }}_{\mathrm{R}}$ for ν_R=20 and 62.5 kHz and $b_{\mathrm{HH}}/\left(\mathit{\pi }\right)$ = (a) 1 kHz, (b, d) 7 kHz and (c) 15 kHz. (e, f) Experimental ¹H → ¹⁵N D-RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\left(\mathrm{tt}\right)$ signal of L-histidine ⋅ HCl as a function of ${\mathit{\nu }}_{\mathrm{1},max}/{\mathit{\nu }}_{\mathrm{R}}$ and $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}/{\mathit{\nu }}_{\mathrm{R}}$ at 18.8 T with ν_R = (e) 40 kHz or (f) 62.5 kHz. In panels (a)–(d) the white star indicates recoupling conditions with minimal rf field leading to maximal transfer efficiency, and the white vertical line mimics the rf field distribution within the coil.

Similar simulations were performed here for ν_R=20 or 62.5 kHz. As seen in Fig. 2a–c, at a given MAS frequency, higher ¹H–¹H dipolar couplings require higher rf field and broader carrier frequency sweep so that the (tt) pulses remain adiabatic in spite of the modulation of the ¹H–¹H dipolar couplings by MAS (Nagashima et al., 2021; Kervern et al., 2007). For $\left|b_{\mathrm{HH}}\right|/\left(\mathrm{2}\mathit{\pi }\right)=\mathrm{7}$ kHz, the minimal ${\mathit{\nu }}_{\mathrm{1},max}/{\mathit{\nu }}_{\mathrm{R}}$ ratio decreases for higher MAS frequencies (compare Fig. 2b and d) since the contribution of the modulation of ¹H–¹H dipolar couplings by MAS to the first adiabaticity factor is proportional to (${\mathit{\nu }}_{\mathrm{1},max}{)}^{\mathrm{2}}/{\mathit{\nu }}_{\mathrm{R}}$; hence, ${\mathit{\nu }}_{\mathrm{1},max}$ values proportional to $\sqrt{{\mathit{\nu }}_{\mathrm{R}}}$, i.e., ${\mathit{\nu }}_{\mathrm{1},max}/{\mathit{\nu }}_{\mathrm{R}}$ ratio inversely proportional to $\sqrt{{\mathit{\nu }}_{\mathrm{R}}}$, are sufficient to maintain the adiabaticity of the pulses (Kervern et al., 2007). Nevertheless, Fig. 2d indicates that the $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) recoupling requires ${\mathit{\nu }}_{\mathrm{1},max}\ge \mathrm{313}$ kHz for ν_R=62.5 kHz, which is hardly compatible with the specifications of most 1.3 mm MAS probes. Similar transfer efficiencies were simulated for the RINEPT sequence with $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) recoupling scheme (not shown).

4 NMR experiments

4.1 Samples and experimental conditions

L-[U-¹⁵N]-histidine ⋅​​​​​​​ HCl (hereafter referred to as “histidine”) and isotopically unmodified γ-alumina were purchased from Merck, and AlPO₄-14 was prepared as described previously (Antonijevic et al., 2006).

All ¹H → S RINEPT-CWc and PRESTO-III experiments were performed at B₀=18.8 T on Bruker BioSpin Avance NEO spectrometers equipped with double-resonance ¹H/X probes.

¹H → ¹⁵N RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) experiments on histidine were performed with 1.3 and 0.7 mm MAS probes spinning at ν_R=40 or 62.5 kHz, with defocusing and refocusing delays equal to τ = 375 and 384 µs, respectively. The rf field of the ¹H $\mathit{\pi }/\mathrm{2}$ and π pulses, which do not belong to the recoupling scheme, was equal to 200 kHz, that of the continuous-wave irradiation to 100 kHz, and that of the ¹⁵N pulses to 62 kHz. ¹H decoupling with an rf field of 16 kHz was applied during the acquisition. The pulses on the ¹H channel were applied on resonance, whereas those on the ¹⁵N channel were applied at the isotropic chemical shift of the ¹⁵NH^τ signal (172 ppm). These 1D spectra resulted from averaging eight transients with a relaxation delay of 3 s. The ¹⁵N isotropic chemical shifts were referenced to an aqueous saturated solution of NH₄NO₃ using [¹⁵N]-glycine as a secondary reference.

Table 1 Comparison of the performances of ¹H → ²⁷Al RINEPT-CWc and PRESTO transfers using various recouplings for AlO₆ signal of γ-alumina at ν_R=20 kHz.

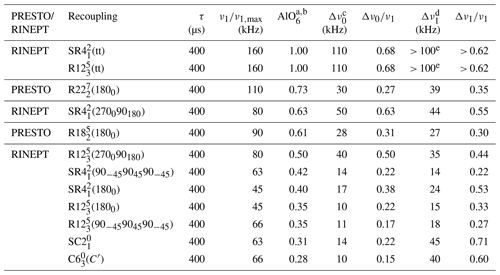
^a AlO₆ signal normalized to that with ¹H → ²⁷Al RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt). ^b The relative error bars were determined from the S $/$ N, for the AlO₆ signal intensity, and they are equal to ±0.03. ^c FWHM (full width at half maximum) of the robustness to offset. ^d FWHM of the robustness to rf field. ^e​​​​​​​ Only a lower bound of rf field could be determined due to probe rf specifications (Fig. 4).

Table 2 Comparison of the performances of ¹H → ²⁷Al RINEPT-CWc and PRESTO transfers with AlPO₄-14 at ν_R=20 kHz.

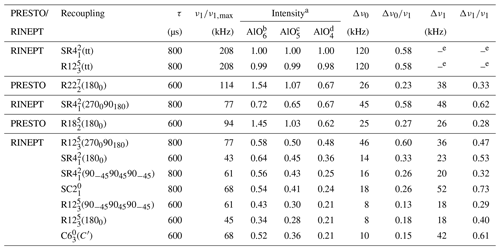
^a Intensities of AlO₆, AlO₅ and AlO₄ resonances normalized to their intensities with ¹H → ²⁷Al RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt). The relative errors for the signal intensities are ^b ± 0.02, ^c ±0.03 and ^d ±0.01, for AlO₆, AlO₅ and AlO₄, respectively. ^e FWHM of the robustness to rf field was not measured for RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) or RINEPT-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) (Fig. S2).

¹H → ²⁷Al RINEPT-CWc and PRESTO-III experiments on γ-alumina and AlPO₄-14 were performed with a 1.3 mm MAS probe spinning at ν_R=20 (to test the $\mathrm{R}{N}_n^{\mathit{\nu }}$ schemes with large rf field requirement) or 62.5 kHz. The tested recoupling schemes are listed in Tables 1 and 2 for ν_R=20 kHz and Tables 3 and 4 for ν_R=62.5 kHz. The rf field of the ¹H $\mathit{\pi }/\mathrm{2}$ and π pulses, which do not belong to the recoupling scheme, was equal to 208 kHz, that of the continuous-wave irradiation to 147 kHz, and the ²⁷Al CT-selective one for $\mathit{\pi }/\mathrm{2}$ and π pulses to 10 kHz. The defocusing and refocusing delays τ are given in Tables 1 to 4. The pulses on the ¹H channel were applied on resonance, whereas those on ²⁷Al channel were applied (i) on resonance with AlO₆ signal of γ-alumina in Figs. 4 and 7, Tables 1 and 3, and in Figs. 5 and 8 when the offset is null; (ii) on resonance with AlO₄ signal of AlPO₄-14 in Figs. S2 and S4, Tables 2 and 4 as well as in Figs. S3 and S5 when the offset is null; and (iii) in the middle of the AlO₄ and AlO₆ peaks for the 1D spectra shown in Figs. 3 and 6. These differences in offset explain some changes in the relative efficiencies of the recoupling between the figures. These 1D spectra resulted from averaging 64 transients with a relaxation delay of 1 s. The ²⁷Al isotropic chemical shifts were referenced at 0 ppm to 1 mol L⁻¹ [Al(H₂O)₆]³⁺ solution.

Table 3 Comparison of the performances of ¹H → ²⁷Al RINEPT-CWc and PRESTO transfers using various recouplings for the AlO₆ signal of γ-alumina at ν_R=62.5 kHz.

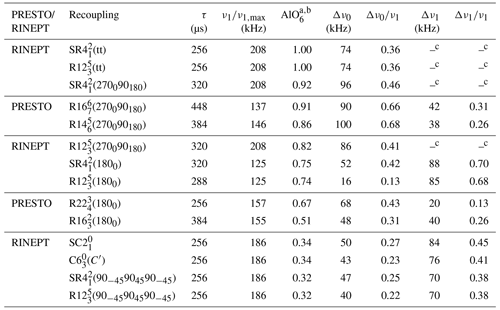
^a AlO₆ signal normalized to that with ¹H → ²⁷Al RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt). ^b The relative error on AlO₆ signal intensity is ±0.08. ^c FWHM of the robustness to rf field was not measured for RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) or RINEPT-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) (Fig. 7).

Table 4 Comparison of the performances of ¹H → ²⁷Al RINEPT-CWc and PRESTO transfers using various recouplings for AlPO₄-14 at ν_R=62.5 kHz.

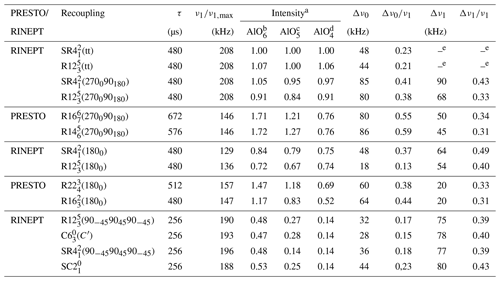
^a Intensities of AlO₆, AlO₅ and AlO₄ resonances normalized to their intensities with ¹H → ²⁷Al RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt). The relative errors for the signal intensities are ^b ±0.04, ^c ±0.06 and ^d ±0.02, for AlO₆, AlO₅ and AlO₄, respectively. ^e FWHM of the robustness to rf field was not measured for RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) or RINEPT-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) (Fig. S4).

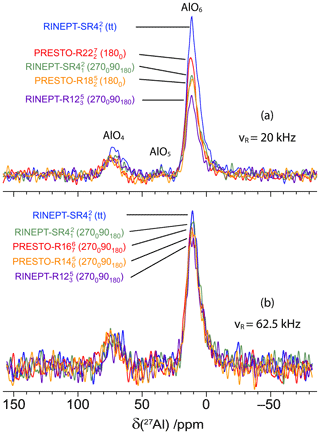
Figure 3 The ²⁷Al 1D spectra of γ-alumina at 18.8 T with ν_R=20 kHz (a) and 62.5 kHz (b) acquired using ¹H → ²⁷Al transfers with RINEPT-CWc and $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\left(\mathrm{tt}\right)$, $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(270₀90₁₈₀), or PRESTO and (a) $\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) or $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀), or (b) $\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) and $\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$(270₀90₁₈₀). The τ delays and ${\mathit{\nu }}_{\mathrm{1}}/{\mathit{\nu }}_{\mathrm{1},max}$ rf fields were fixed to their optimum values given in Tables 1 and 3.

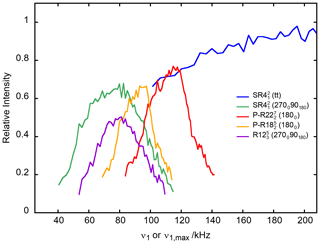
Figure 4 The ²⁷AlO₆ on-resonance signal of γ-alumina at ν_R=20 kHz as a function of ν₁ or ${\mathit{\nu }}_{\mathrm{1},max}$ for PRESTO-$\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) and PRESTO-$\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀) as well as RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt), RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and RINEPT-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$ (270₀90₁₈₀). For each curve, τ was fixed to its optimum value given in Table 1.

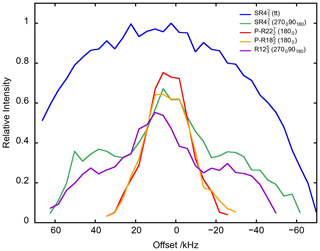
Figure 5 The ²⁷AlO₆ signal of γ-alumina at ν_R=20 kHz as a function of offset for PRESTO-$\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) and PRESTO-$\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀) as well as RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt), RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and RINEPT-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(270₀90₁₈₀). For each curve, τ and ν₁ or ${\mathit{\nu }}_{\mathrm{1},max}$ were fixed to their optimum values given in Table 1.

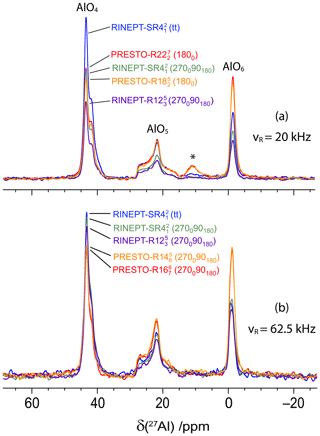
Figure 6 The ²⁷Al 1D spectra of AlPO₄-14 at 18.8 T with ν_R=20 kHz (a) and 62.5 kHz (b) acquired using ¹H → ²⁷Al transfers with RINEPT-CWc and $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}\left(\mathrm{tt}\right)$, $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(270₀90₁₈₀), or PRESTO and (a) $\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) and $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀), or (b) $\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) and $\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$(270₀90₁₈₀). The τ delays and ${\mathit{\nu }}_{\mathrm{1}}/{\mathit{\nu }}_{\mathrm{1},max}$ rf fields were fixed to their optimal values given in Tables 2 and 4. The resonance at ca. 11 ppm in panel (a) is due to an impurity.

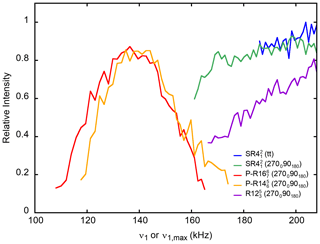
Figure 7 The ²⁷AlO₆ on-resonance signal of γ-alumina at ν_R=62.5 kHz as a function of ν₁ or ${\mathit{\nu }}_{\mathrm{1},max}$ for PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) and PRESTO-$\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$(270₀90₁₈₀) as well as RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt), RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and RINEPT-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(270₀90₁₈₀). For each curve, τ was fixed to its optimum value given in Table 3.

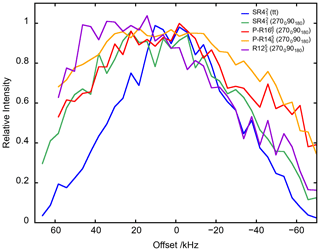
Figure 8 The ²⁷AlO₆ signal of γ-alumina at ν_R=62.5 kHz as a function of offset for PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) and PRESTO-$\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$(270₀90₁₈₀) as well as RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt), RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and RINEPT-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(270₀90₁₈₀). For each curve, τ and ν₁ or ${\mathit{\nu }}_{\mathrm{1},max}$ were fixed to their optimum values given in Table 3.

We also measured the decay of the transverse proton magnetization of AlPO₄-14 during a spin echo sequence, in which the refocusing π pulse was identical to that used in the defocusing part of the RINEPT-CWc sequences (Fig. 1b). This decay was measured at ν_R=20 and 62.5 kHz either without any recoupling or by applying a $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ recoupling built from (180₀), (270₀90₁₈₀) and (tt) pulses during the delays of the spin echo sequence. The rf fields during the recoupling two blocks were equal to their optimal values given in Tables 2 and 4.

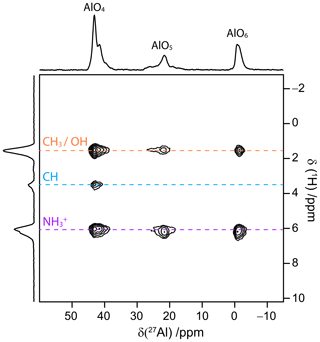
We also acquired several 2D ¹H → ²⁷Al D-HETCOR spectra of AlPO₄-14 using RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ with (180₀), (270₀90₁₈₀) and (tt) pulses as well as PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀). These 2D spectra were acquired using a non-uniform sampling (NUS) with an exponentially biased sampling retaining 25 % of the points with respect to uniform sampling. The 2D spectra resulted from eight transients for each of the 500 t₁ increments with a recycle delay of 1 s, i.e., an acquisition time of 72 min.

4.2 Optimal adiabatic recoupling

Figure 2e and f show the efficiency of the ¹H → ¹⁵N RINEPT-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) transfer for histidine as a function of the ${\mathit{\nu }}_{\mathrm{1},max}/{\mathit{\nu }}_{\mathrm{R}}$ and $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}/{\mathit{\nu }}_{\mathrm{R}}$ ratios for ν_R = 40 or 62.5 kHz, respectively. These experimental data indicate that at higher MAS frequencies, an efficient adiabatic recoupling can be achieved for lower ${\mathit{\nu }}_{\mathrm{1},max}/{\mathit{\nu }}_{\mathrm{R}}$ and $\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{0},max}/{\mathit{\nu }}_{\mathrm{R}}$ ratios. This result agrees with the numerical simulations of Fig. 2b and d.

4.3 PRESTO and RINEPT performances for ν_R=20 kHz

4.3.1 γ-alumina

The 1D spectra of γ-alumina acquired using ¹H → ²⁷Al RINEPT and PRESTO sequences, shown in Fig. 3, exhibit two resonances at 70 and 10 ppm, assigned to tetra- (AlO₄) and hexa-coordinated (AlO₆) resonances, respectively (Morris and Ellis, 1989). The signal of penta-coordinated (AlO₅) sites, which are mainly located in the first surface layer, is barely detected because of the lack of sensitivity of conventional solid-state NMR spectroscopy (Lee et al., 2014). The most intense peak, AlO₆, was used to compare the transfer efficiencies of RINEPT and PRESTO sequences with different recoupling schemes. Table 1 lists the measured performances of ¹H → ²⁷Al RINEPT-CWc and PRESTO transfers using various recoupling for γ-alumina at ν_R=20 kHz. We notably compared the PRESTO sequences using $\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) and $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀) recoupling with the RINEPT-CWc scheme using $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ and $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$ with single (180₀), composite (270₀90₁₈₀), and (90₋₄₅90₄₅90₋₄₅) or (tt) adiabatic pulses. A low transfer efficiency was obtained for RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(90₀240₉₀90₀) because of its low scaling factor, κ = 0.131; hence, its performances are not reported in Table 1. We also tested the recoupling schemes based on the symmetry $\mathrm{SC}{\mathrm{2}}_{\mathrm{1}}^{\mathrm{0}}$, corresponding to the ${\left[\mathrm{C}{\mathrm{2}}_{\mathrm{1}}^{\mathrm{0}}\right]}_{\mathrm{0}}{\left[\mathrm{C}{\mathrm{2}}_{\mathrm{1}}^{\mathrm{0}}\right]}_{\mathrm{120}}{\left[\mathrm{C}{\mathrm{2}}_{\mathrm{1}}^{\mathrm{0}}\right]}_{\mathrm{240}}$ sequence with a basic element C = (90₄₅90₁₃₅90₄₅90₂₂₅90₃₁₅90₂₂₅) or $\mathrm{C}{\mathrm{6}}_{\mathrm{3}}^{\mathrm{0}}$ built from C^′ = (90₃₀90₁₂₀90₃₀90₂₄₀90₃₃₀90₂₄₀). These basic elements, which derive from (90₋₄₅90₄₅90₋₄₅), have recently been proposed (Perras et al., 2019). As seen in Table 1 and Fig. 3a, the sequences yielding the highest transfer efficiencies are by decreasing order RINEPT-CWc with $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) or $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) > PRESTO-$\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) > RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) ≈ PRESTO-$\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀) > RINEPT-CWc-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(270₀90₁₈₀). Figures 4 and 5 display the signal intensity of these sequences as a function of the rf field amplitude and offset, respectively.

The highest transfer efficiencies are obtained with the RINEPT-CWc sequence incorporating a (tt) adiabatic pulse. This recoupling also leads to the highest robustness to offset and rf inhomogeneity, and $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) and $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) yield identical transfer efficiency and robustness. Hence, the three-step multiple-quantum super-cycle of the $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ symmetry does not improve the robustness in the case of a (tt) basic element. However, these recoupling schemes require maximum rf fields of ${\mathit{\nu }}_{\mathrm{1},max}\ge \mathrm{8}{\mathit{\nu }}_{\mathrm{R}}=$ 160 kHz, which may exceed the rf power specifications of most 3.2 mm MAS probes.

The PRESTO sequences using $\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) and $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀) recoupling also result in good transfer efficiencies but lower than RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt). However, they use rf fields of ${\mathit{\nu }}_{\mathrm{1}}/{\mathit{\nu }}_{\mathrm{R}}=$ 5.5 and 4.5, which are compatible with the specifications of 3.2 mm MAS probes. The higher transfer efficiency of $\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) with respect to $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀) stems from its weaker second-order cross terms between ¹H–¹H interactions (Table S1).

The efficiency of the RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) sequence, with ν₁=4ν_R, is comparable to that of PRESTO-$\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀) but with a higher robustness to offset and rf inhomogeneity. We can notice that amplitude modulated recoupling schemes, for which the phase shifts are equal to 180^∘, such as $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(180₀), exhibit a high robustness to rf field maladjustments (Fig. 5) (Carravetta et al., 2000). The use of (270₀90₁₈₀) composite pulses with $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ symmetry, instead of single π pulses, improves its transfer efficiency as well as its robustness to offset and rf field inhomogeneity.

In summary, for ν_R=20 kHz in γ-alumina, the RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) sequence achieves efficient and robust transfers of magnetization from protons to ²⁷Al nuclei using a moderate rf field of ν₁=4ν_R. For ¹H spectra with a width smaller than 20 kHz and MAS probes with a good rf homogeneity, PRESTO-$\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) can result in slightly higher transfer efficiencies.

4.3.2 AlPO₄-14

Figure 6a shows the ¹H → ²⁷Al RINEPT and PRESTO 1D spectra of AlPO₄-14 recorded with ν_R=20 kHz. They exhibit three ²⁷Al resonances at 43, 21 and −2 ppm assigned to AlO₄, AlO₅ and AlO₆ sites, respectively (Ashbrook et al., 2008) The AlO₅ and AlO₆ sites are directly bonded to OH groups. The ¹H MAS spectrum is shown in Fig. S1. According to the literature, the ²⁷AlO₄ signal subsumes the resonances of two AlO₄ sites with quadrupolar coupling constants C_Q = 1.7 and 4.1 MHz, whereas those of AlO₅ and AlO₆ sites are equal to 5.6 and 2.6 MHz, respectively (Fernandez et al., 1996; Antonijevic et al., 2006). The ¹H–¹H dipolar couplings within the isopropylamine template molecule are larger than in γ-alumina. We used the most intense peak, AlO₄, to compare the ¹H → ²⁷Al transfer efficiencies of RINEPT-CWc and PRESTO sequences with different recoupling schemes, and the results are given in Table 2. The six sequences yielding the highest transfer efficiencies are the same as for γ-alumina and their relative efficiencies are comparable for the AlO₄ peak of AlPO₄-14 and the AlO₆ signal of γ-alumina.

Nevertheless, the rf requirement of the $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) and $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) schemes is higher for AlPO₄-14 than for γ-alumina because of the larger ¹H–¹H dipolar couplings, in agreement with the numerical simulations of Fig. 2a–c. This rf requirement prevents the use of these adiabatic recoupling schemes at ν_R=20 kHz with most 3.2 mm MAS probes. That of the other sequences and their robustness to offset and rf field homogeneity are similar for both samples (Table 2 and Figs. S2 and S3).

In the case of AlPO₄-14, PRESTO yields a higher efficiency than RINEPT for AlO₅ and AlO₆, contrary to the AlO₄ resonance, since (i) these Al sites are directly bonded to OH groups and (ii) $\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) and $\mathrm{R}{\mathrm{18}}_{\mathrm{2}}^{\mathrm{5}}$(180₀) schemes are subject to dipolar truncation (Sect. 2.1.1), which prevents to transfer the ¹H magnetization of these OH groups to ²⁷AlO₄ nuclei.

Hence, at ν_R=20 kHz, for both AlPO₄-14 and γ-alumina, the RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and PRESTO-$\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) sequences are the best choices to transfer the ¹H magnetization to ²⁷Al nuclei.

4.4 PRESTO and RINEPT performances for ν_R=62.5 kHz

Similar comparisons of the performances of the various RINEPT-CWc and PRESTO sequences were performed for γ-alumina and AlPO₄-14 at ν_R=62.5 kHz.

4.4.1 γ-alumina

The corresponding data for γ-alumina are given in Table 3. The sequences yielding the highest transfer efficiencies are by decreasing order: RINEPT-CWc with $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) or $\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(tt) > RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) ≈ PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) > PRESTO-$\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$(270₀90₁₈₀) > RINEPT-CWc-$\mathrm{R}{\mathrm{12}}_{\mathrm{3}}^{\mathrm{5}}$(270₀90₁₈₀).

The nominal rf requirements of the RINEPT sequences using adiabatic or (270₀90₁₈₀) composite π pulses correspond to ${\mathit{\nu }}_{\mathrm{1},max}\approx \mathrm{5}{\mathit{\nu }}_{\mathrm{R}}$ (313 kHz: Fig. 2d) or 4ν_R (250 kHz), which exceed the specifications of our 1.3 mm MAS probe, and the sequences were tested only up to ${\mathit{\nu }}_{\mathrm{1},max}=\mathrm{208}$ kHz (Fig. 7). This suboptimal rf field may limit the transfer efficiencies of these sequences.

The PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) and PRESTO-$\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$(270₀90₁₈₀) sequences yield transfer efficiencies comparable to those of RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) but with a significantly lower rf field, ν₁≈137 kHz ≈2.3ν_R. Furthermore, the robustness to offset of these PRESTO sequences is comparable to that of RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) (Fig. 8). PRESTO-$\mathrm{R}{\mathrm{22}}_{\mathrm{4}}^{\mathrm{3}}$(180₀) and PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{3}}^{\mathrm{2}}$(180₀) sequences with a small phase shift of 2ϕ≤52^∘ are less efficient, because they are sensitive to rf inhomogeneity.

4.4.2 AlPO₄-14

In the case of AlPO₄-14, the relative transfer efficiencies for ²⁷AlO₄ species follow a similar order as for γ-alumina, except that the transfer efficiencies of PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) and PRESTO-$\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$(270₀90₁₈₀) are significantly lower than that of RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) (Table 4). This decreased efficiency of the PRESTO schemes for AlO₄ stems notably from the dipolar truncation, which prevents the transfer of magnetization from the OH groups bonded to AlO₅ and AlO₆ sites to AlO₄, since these ²⁷AlO₄ nuclei are significantly more distant from protons (see Table S5). Furthermore, the amplitude-modulated $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) recoupling benefits from a higher robustness to rf field inhomogeneity than the PRESTO schemes (Fig. S4). Conversely, the robustness to offset of these three sequences are comparable (Fig. S5), whereas the rf requirements of $\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) and $\mathrm{R}{\mathrm{14}}_{\mathrm{6}}^{\mathrm{5}}$(270₀90₁₈₀) are much lower than that of $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀).

In summary, at ν_R=62.5 kHz, for both γ-alumina and isopropylamine-templated AlPO₄-14, PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) and RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) are the best methods to transfer the polarization of protons to quadrupolar nuclei. However, the first sequence requires a much lower rf field than the second does.

4.5 Decay of transverse ¹H magnetization during recoupling

We also measured the decay of the ¹H transverse magnetization during a spin echo experiment, in which the refocusing π pulse was the composite one employed in the defocusing part of the RINEPT-CW sequence shown in Fig. 1b. We performed these experiments on AlPO₄-14 since the ¹H–¹H dipolar interactions are larger in this sample than in γ-alumina. This decay was measured either in the absence of any recoupling or under a $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ recoupling built from (180₀), (270₀90₁₈₀) or (tt) inversion element. The three ¹H signals featured a mono-exponential decay with a time constant $T_{\mathrm{2}}^{\prime }$ reported in Table 5.

Table 5 The ¹H $T_{\mathrm{2}}^{\prime }$ values of AlPO₄-14 without recoupling or with $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$ recoupling built from (180₀), (270₀90₁₈₀) or (tt) inversion elements. The estimated error bars are equal to 7 %.

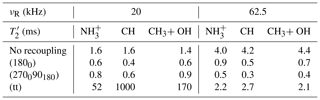
At ν_R=20 kHz, the $T_{\mathrm{2}}^{\prime }$ constants are significantly shorter under $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(180₀) and $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) than without recoupling. This faster decay can stem from the reintroduction of ¹H–¹H dipolar interactions in the second- and higher-order terms of the AH by the recoupling as well as the effect of pulse transients (Wittmann et al., 2016). Conversely, the $T_{\mathrm{2}}^{\prime }$ constants under $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) are much longer than without recoupling, showing that the adiabatic pulses using large rf field efficiently decouple the ¹H–¹H dipolar interactions, whereas the continuous variation of the phase and amplitude during these pulses minimizes the transients.

At ν_R=62.5 kHz, the $T_{\mathrm{2}}^{\prime }$ constants without recoupling are lengthened with respect to those at ν_R=20 kHz since faster MAS better averages the ¹H–¹H dipolar interactions (Mao et al., 2009). Conversely, the $T_{\mathrm{2}}^{\prime }$ constants under $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) recoupling are shorter at ν_R=62.5 than at 20 kHz. This counterintuitive reduction may stem from the shorter pulse lengths at ν_R=62.5 kHz, which result in a larger number of transients. Indeed, the recoupling time, τ, only depends on the sample; hence, the number of transients is proportional to ν_R, because the recoupling sequences are rotor synchronized. Moreover, it also increases with the use of composite pulses and as a result there are 6.25 times more transients at ν_R=62.5 kHz and (270₀,90₁₈₀) pulses than at 20 kHz MAS and (180₀) pulses. Additionally, the rf power increases with the spinning speed and the use of composite pulses, and then also the amplitude of the transients. For the same reason, the $T_{\mathrm{2}}^{\prime }$ constants under $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(180₀) are only slightly longer at high MAS frequency. The $T_{\mathrm{2}}^{\prime }$ constants under $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) recoupling are much shorter at ν_R=62.5 than at 20 kHz, because the adiabaticity criterion is not fulfilled at ν_R=62.5 kHz; hence, the elimination of ¹H–¹H dipolar interactions is less effective (Figs. 2f and S4).

4.6  2D ¹H–²⁷Al D-HETCOR of AlPO₄-14

Figure 9 demonstrates the possibility to acquire 2D ¹H–²⁷Al D-HETCOR spectra using RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀,90₁₈₀) transfer at ν_R=62.5 kHz. This spectrum was recorded using a NUS scheme retaining 25 % of the t₁ points, which would be acquired using uniform sampling. In this spectrum, the CH proton only correlates with the AlO₄ site since it is too distant from AlO₅ and AlO₆ sites (see Table S5). The other two ¹H signals correlate with the three Al environments. Similar 2D spectra (not shown) were acquired using RINEPT-CWc transfer based on $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(180₀) and $\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) recoupling as well as PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀). Their skyline projections are shown in Figs. S6 and S7.

Figure 9 The ¹H–²⁷Al D-HETCOR 2D spectrum of AlPO₄-14, along with its skyline projections, at B₀ = 18.8 T and ν_R=62.5 kHz acquired in only 72 min with only ca. 2.5 µL of active volume with NUS 25 % using RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) transfer.

5 Conclusions

In this work, we have introduced novel symmetry-based heteronuclear dipolar recoupling schemes, which can be incorporated into the RINEPT and PRESTO sequences to transfer the magnetization from protons to half-integer quadrupolar nuclei at ν_R=20 or 62.5 kHz. These new recouplings have been compared to the existing ones. We have shown that the RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(tt) sequence with adiabatic pulses, which produces efficient and robust transfers at ν_R≈10–15 kHz (Nagashima et al., 2020), requires rf fields incompatible with the specifications of most MAS probes for ν_R≥20 kHz. Conversely, the introduced RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and PRESTO-$\mathrm{R}{\mathrm{22}}_{\mathrm{2}}^{\mathrm{7}}$(180₀) techniques with rf fields of ca. 4ν_R and 5.5ν_R, respectively, are the methods of choice at ν_R=20 kHz to transfer the magnetization from protons to quadrupolar nuclei. At ν_R=62.5 kHz, the RINEPT-CWc-$\mathrm{SR}{\mathrm{4}}_{\mathrm{1}}^{\mathrm{2}}$(270₀90₁₈₀) and PRESTO-$\mathrm{R}{\mathrm{16}}_{\mathrm{7}}^{\mathrm{6}}$(270₀90₁₈₀) sequences with rf requirements of ca. 4ν_R and 2.3ν_R, respectively, result in the most robust and efficient transfers. At both MAS frequencies, the RINEPT and PRESTO techniques complement each other since the latter is dipolar truncated, whereas the former is not. As a result, the RINEPT sequences must be chosen to observe simultaneously protonated and unprotonated sites, whereas the PRESTO schemes can be employed for the selective observation of quadrupolar nuclei in proximity to protons. These techniques are expected to be useful for transferring the DNP-enhanced magnetization of protons to quadrupolar nuclei in indirect MAS DNP experiments at ν_R≥20 kHz, notably used at high magnetic fields (Nagashima et al., 2021, 2020; Rankin et al., 2019; Berruyer et al., 2020). We also show that they can be used to correlate the NMR signals of protons and quadrupolar nuclei at high MAS frequencies.