Solid-state ¹H spin polarimetry by ¹³CH₃ nuclear magnetic resonance

Dissolution dynamic nuclear polarization is used to prepare nuclear spin polarizations approaching unity. At present, ¹H polarization quantification in the solid state remains fastidious due to the requirement of measuring thermal equilibrium signals. Line shape polarimetry of solid-state nuclear magnetic resonance spectra is used to determine several useful properties regarding the spin system under investigation. In the case of highly polarized nuclear spins, such as those prepared under the conditions of dissolution dynamic nuclear polarization experiments, the absolute polarization of a particular isotopic species within the sample may be directly inferred from the characteristics of the corresponding resonance line shape. In situations where direct measurements of polarization are complicated by deleterious phenomena, indirect estimates of polarization using coupled heteronuclear spins prove informative. We present a simple analysis of the ¹³C spectral line shape of [2-¹³C]sodium acetate based on the normalized deviation of the centre of gravity of the ¹³C peaks, which can be used to indirectly evaluate the proton polarization of the methyl group moiety and very likely the entire sample in the case of rapid and homogeneous ¹H–¹H spin diffusion. For the case of positive microwave irradiation, ¹H polarization was found to increase with an increasing normalized centre of gravity deviation. These results suggest that, as a dopant, [2-¹³C]sodium acetate could be used to indirectly gauge ¹H polarizations in standard sample formulations, which is potentially advantageous for (i) samples polarized in commercial dissolution dynamic nuclear polarization devices that lack ¹H radiofrequency hardware, (ii) measurements that are deleteriously influenced by radiation damping or complicated by the presence of large background signals and (iii) situations where the acquisition of a thermal equilibrium spectrum is not feasible.

1 Introduction

Classical nuclear magnetic resonance (NMR) experiments produce inherently weak signals. The severely limiting low intrinsic sensitivity of the technique can be enhanced by up to 4 orders of magnitude by employing a wide range of routinely used hyperpolarization methodologies (Ardenkjær-Larsen et al., 2003; Hirsch et al., 2015; Dale and Wedge, 2016; Meier, 2018; Kouřil et al., 2019). The significantly boosted NMR signal intensities from metabolites hyperpolarized by implementing a dissolution dynamic nuclear polarization (dDNP) approach have been used in the characterization of cancer in human patients (Nelson et al., 2013; Chen et al., 2020; Gallagher et al., 2020).

To hyperpolarize nuclear spins via the dDNP approach, the spin system of interest is co-frozen in a mixture of aqueous solvents and glassing agents with a carefully chosen paramagnetic radical species (Abragam and Goldman, 1978). The dDNP-compatible solution is subsequently frozen at liquid-helium temperatures (where the solvent matrix forms a glass) inside a magnetic field and is irradiated with slightly off-resonant (with respect to the centre of electron spin transition) microwaves, which transfer the high electron spin polarization to the nuclear spins of interest (Kundu et al., 2019).

Hyperpolarization of methyl group moieties by dDNP has led to some unusual effects including the generation of long-lived spin order, which is revealed in the liquid state upon dissolution of the material from cryogenic conditions (Meier et al., 2013; Roy et al., 2015; Dumez et al., 2017; Elliott et al., 2018). Solid-state NMR of highly polarized nuclear spins has previously been utilized to infer the sample polarization level and, in suitable cases, the quantity of long-lived spin order established (Waugh et al., 1987; Kuhns et al., 1989; Marohn et al., 1995; Kuzma et al., 2013; Mammoli et al., 2015; Willmering et al., 2017; Elliott et al., 2018; Aghelnejad et al., 2020). To the best of our knowledge, the solid-state NMR spectra of strongly polarized methyl groups have not shown any significant features which may be used for a clear line shape analysis.

In this communication, we propose that the ¹³C NMR line shape of [2-¹³C]sodium acetate can be used to indirectly quantify the ¹H polarization of the methyl group spins. Furthermore, since ¹H–¹H spin diffusion rapidly achieves a homogeneous proton polarization across the entire sample, the ¹H polarization level of the whole sample is therefore likely to be reflected by the ¹H polarization of the methyl group moiety. We analyse the experimental ¹³C NMR spectra acquired for different ¹H polarizations and herein present a straightforward approach to indirectly quantify the ¹H polarization based on the ¹³C NMR peak normalized deviation of the centre of gravity (CoG). ¹H polarization was observed to increase with an increasing ¹³C NMR peak CoG deviation (case of positive microwave irradiation).

2 Methods

2.1 Sample preparation

A solution of 3 M [2-¹³C]sodium acetate in the glass-forming mixture H₂O/D₂O/glycerol-d₈ (1/3/6 $v/v/v$) was doped with 50 mM TEMPOL radical (all compounds purchased from Sigma-Aldrich) and sonicated for ∼ 10 min. Paramagnetic TEMPOL radicals were chosen to polarize ¹H spins most efficiently under our dDNP conditions.

2.2 Sample freezing

A 100 µL volume of the above sample was pipetted into a Kel-F sample cup and inserted into a 7.05 T prototype Bruker Biospin polarizer equipped with a specialized dDNP probe, including a background-free radiofrequency (rf) coil insert (Elliott et al., 2021a), running TopSpin 3.5 software. The sample temperature was reduced to 1.2 K by submerging the sample in liquid helium and reducing the pressure of the variable temperature insert (VTI) towards ∼ 0.7 mbar.

2.3 Dynamic nuclear polarization

The 100 µL of sample was polarized by applying microwave irradiation at f_μw=197.616 GHz (positive lobe of the DNP enhancement profile) or f_μw=198.192 GHz (negative lobe of the DNP enhancement profile) with triangular frequency modulation (Bornet et al., 2014) of amplitude $\mathrm{\Delta }{f}_{\mathit{\mu }\mathrm{w}}=\pm \mathrm{136}$ MHz or $\mathrm{\Delta }{f}_{\mathit{\mu }\mathrm{w}}=\pm \mathrm{112}$ MHz, respectively, and rate f_mod=0.5 kHz at a power of ca. 125 mW at the output of the microwave source (value given by the provider of our microwave source VDI/AMC 705) and ca. 30 mW reaching the DNP cavity (evaluated by monitoring the helium bath pressure; see Sect. 2.4), which were optimized prior to commencing experiments to achieve the highest possible level of ¹H polarization.

2.4 Microwave power evaluation

The microwave power reaching the DNP cavity was determined by comparison with the heating from a resistor in the liquid helium bath and calibrating how much the bath pressure increases vs. microwave power. In practice, the measurement was performed as follows:

• i.

  The VTI was filled with liquid helium and pumped down to 0.65 mbar, corresponding to 1.2 K.

• ii.

  The change of pressure when turning on a resistive heater or the microwave source for 120 s was monitored. The pressure plateaus after approximatively 60 s.

• iii.

  The pressure difference between the base pressure and that under the effect of the resistive heater or the microwave source ΔP_mbar is calculated.

All measurements were performed ensuring that the liquid helium level in the VTI was not varying by more than a few centimetres: the microwave cavity was immersed under 5–10 cm of liquid helium. The measurements performed using the resistive heater with power P_heater are used to plot a calibration curve P_heater vs. ΔP_mbar with slope a. The deposited microwave power in the cavity is then obtained by computing P_microwave=aΔP_mbar.

2.5 Polarization build-ups

To monitor ¹³C NMR spectral line shapes with satisfactory signal-to-noise ratios (SNRs), ¹³C polarization must first be built-up by using a succession of optimized cross-polarization (CP) contact rf pulses. Then, to observe changes in the line shape of ¹³C NMR spectra acquired as the ¹H polarization builds up from the thermal to DNP equilibrium, we employed a series of ¹H saturating rf pulses followed by microwave activation, a small flip-angle rf pulse and ¹³C NMR signal detection, as shown by the rf pulse sequence shown in Fig. 1. The build-up of ¹³C polarization throughout the microwave irradiation period was tracked by engaging the following experimental procedure:

• i.

  A saturating sequence of 90^∘ rf pulses with alternating phases separated by a short delay (typically (typ.) 11 ms) repeated n times (typ. n=50) kills residual magnetization on both rf channels.

• ii.

  The microwave source becomes active and ¹H polarization builds up.

• iii.

  The ¹³C Zeeman magnetization trajectory is minimally perturbed by the application of a small flip-angle rf pulse (typ. β = 3.5^∘) used for detection, which is then followed by a short acquisition period (typ. t_FID = 1 ms).

• iv.

  ¹H DNP builds up during a time $t_{\mathrm{DNP}}^{\mathrm{1}}$ (typ. $t_{\mathrm{DNP}}^{\mathrm{1}}$ = 30 s).

• v.

  Stages (iii)–(iv) are cycled m times (typ. m = 6) in order to monitor the evolution of the ¹³C polarization (between CP steps).

• vi.

  The microwave source is gated, and a delay of duration t_G = 0.5 s occurs (see Sect. 2.6), thus permitting the electron spins to relax to their highly polarized thermal equilibrium state before the next CP step (Bornet et al., 2016).

• vii.

  Two synchronized adiabatic half-passages (AHPs) simultaneously produce transverse magnetization for all pulsed spin species.

• viii.

  The nuclear magnetization is subsequently spin-locked on both rf channels (typically by a high-power rf pulse with a nutation frequency of the order of 15 kHz and a duration between 1–10 ms) and ¹H → ¹³C polarization transfer occurs (Bornet et al., 2016).

• ix.

  A second pair of harmonized AHPs (operating with reverse chronology) restores Zeeman magnetization on each rf channel.

• x.

  Stages (ii)–(ix) are repeated in L units (typ. L = 8) to periodically transfer ¹H Zeeman polarization to ¹³C nuclear spins.

• xi.

  A second saturating sequence of 90^∘ rf pulses with alternating phases separated by a short delay (typ. 11 ms) repeated n times (typ. n = 50) kills residual magnetization on the ¹H rf channel only.

• xii.

  The microwave source reactivates.

• xiii.

  The ¹³C Zeeman magnetization trajectory is minimally perturbed by the application of a small flip-angle rf pulse (typ. β = 3.5^∘) used for detection, which is then followed by a short acquisition period (typ. t_FID = 1 ms).

• xiv.

  ¹H DNP builds up during a time $t_{\mathrm{DNP}}^{\mathrm{2}}$ (typ. $t_{\mathrm{DNP}}^{\mathrm{2}}$ = 5 s).

• xv.

  Stages (xiii)–(xiv) are cycled p times (typ. p = 80) to monitor the evolution of the ¹³C NMR spectra as a function of the ¹H polarization build-up with sufficient SNR.

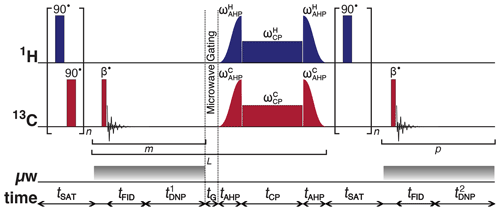
Figure 1 Schematic representation of the rf pulse sequence used to accrue ¹³C polarizations and monitor ¹³C line shapes as a function of the ¹H polarization. The experiments used the following key parameters chosen to maximize the efficiency of the rf pulse sequence: n = 50; β = 3.5^∘; m = 6; $t_{\mathrm{DNP}}^{\mathrm{1}}$ = 30 s; L = 8; t_G = 0.5 s; p = 80; and $t_{\mathrm{DNP}}^{\mathrm{2}}$ = 5 s. AHP =  adiabatic half-passage. AHP sweep width = 100 kHz. The $\mathit{\pi }/\mathrm{2}$ saturating rf pulses used an empirically optimized 13-step phase cycle to remove residual magnetization at the beginning of each experiment: {0, $\mathit{\pi }/\mathrm{18}$, $\mathrm{5}\mathit{\pi }/\mathrm{18}$, $\mathit{\pi }/\mathrm{2}$, $\mathrm{4}\mathit{\pi }/\mathrm{9}$, $\mathrm{5}\mathit{\pi }/\mathrm{18}$, $\mathrm{8}\mathit{\pi }/\mathrm{9}$, π, $\mathrm{10}\mathit{\pi }/\mathrm{9}$, $\mathrm{13}\mathit{\pi }/\mathrm{9}$, $\mathit{\pi }/\mathrm{18}$, $\mathrm{5}\mathit{\pi }/\mathrm{3}$, $\mathrm{35}\mathit{\pi }/\mathrm{18}\mathit{\}}$. The resonance offset was placed at the most intense peak of the ¹H and ¹³C NMR spectra.

Further details regarding multiple-contact CP rf pulse sequence operation are given elsewhere (Bornet et al., 2016). It should be stressed that the use of CP is purely optional, and in most cases its use will be dictated by the rf hardware available. We use CP here simply as a means to offer greater SNRs for ¹³C NMR signal detection. Given the level of sample deuteration, at 6.7 T and with microwave modulation suitable SNRs can also be achieved with direct ¹³C DNP (Cheng et al., 2013).

Since it is unlikely that the ¹³C NMR line shape is significantly influenced by the ¹³C polarization, we can afford not to diminish the ¹³C NMR signal intensity by a sequence of ¹³C saturating rf pulses on the ¹³C rf channel at stage (xi) to maintain high SNRs. The small rf pulse flip angles are necessary to preserve the ¹H and ¹³C polarizations throughout the course of the build-up experiment.

2.6 Microwave gating

Microwave gating was employed shortly before and during CP experiments to allow the electron spin ensemble to return to a highly polarized state, which happens on the timescale of the longitudinal electron relaxation time (typ. T_1e = 100 ms with P_e = 99.93 % under our experimental dDNP conditions) (Bornet et al., 2016). Microwave gating hence provides a way to strongly attenuate paramagnetic relaxation, and consequently the ¹H and ¹³C T_1ρ relaxation time constants in the presence of an rf field are extended by orders of magnitude. This allows spin-locking rf pulses to be much longer, which significantly increases the efficiency of nuclear polarization transfer.

3 Results

3.1 ¹³C CP build-ups and decays

The CP build-up curves for the ¹³C polarizations P_C as a function of the ¹H DNP time t_DNP for both positive and negative microwave irradiation are shown in Fig. 2. The ¹³C polarizations P_C were accrued by employing the rf pulse sequence shown in Fig. 1. The ¹³C polarizations P_C ultimately reached P_C ≃ 40.6 % and P_C ≃ −46.8 % after 8 CP transfers and 24 min of positive and negative microwave irradiation, respectively. The achieved levels of ¹³C polarization P_C are lower than those previously reported in the literature (Bornet et al., 2016) but were not further optimized since only the ¹³C NMR line shape was of interest in this study as a probe for absolute ¹H polarization. This is inconsequential for the current study since sufficient SNRs of the order of ∼ 965 and ∼ 1244 were achieved for the cases of positive and negative microwave irradiation, respectively. After this point, i.e., beyond the vertical dashed line (¹H DNP time = 24 min), a slow and partial decay of the ¹³C NMR signal intensity towards a pseudo-equilibrium is observed; see Fig. 2. This ¹³C NMR signal decay is not a problem in general since the ¹³C NMR signal remains sufficiently intense as to allow clear measurement of the ¹³C NMR line shape with high accuracy.

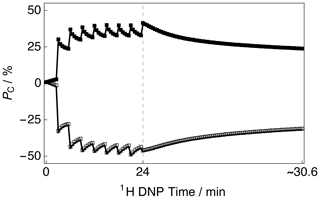
Figure 2 Experimental ¹³C polarization P_C CP build-up curves and subsequent ¹³C signal decays as a function of ¹H DNP time acquired at 7.05 T (¹H nuclear Larmor frequency = 300.13 MHz, ¹³C nuclear Larmor frequency = 75.47 MHz) and 1.2 K with a single transient per data point. The presented data were acquired by using the rf pulse sequence depicted in Fig. 1. Black filled squares: positive microwave irradiation; black empty squares: negative microwave irradiation. The vertical dashed line denotes the ¹H DNP time at which the ¹H NMR signal was destroyed by a second series of saturating rf pulses (as shown by the rf pulse sequence illustrated in Fig. 1).

3.2 ¹³C NMR spectra

Figure 3 shows the relevant part of the experimental ¹³C NMR spectra acquired with a small flip angle rf pulse (β = 3.5^∘) at two different ¹H DNP times. The ¹³C NMR spectra in Fig. 3 were acquired by using the rf pulse sequence shown in Fig. 1. The initial ¹³C NMR spectrum (acquired at 24 min) has a linewidth at full-width half-maximum height (FWHM) of ∼ 10.9 kHz. The ¹³C NMR line shape is relatively symmetrical and has no obvious defining features; see Fig. 3a. Small peak contributions to the ¹³C NMR spectrum are observed towards the baseline, including one environment shifted as much as ca. −300 ppm. This spectrum corresponds to a low level of ¹H polarization ($\left|P_{\mathrm{H}}\right|$ ≃ 0 %).

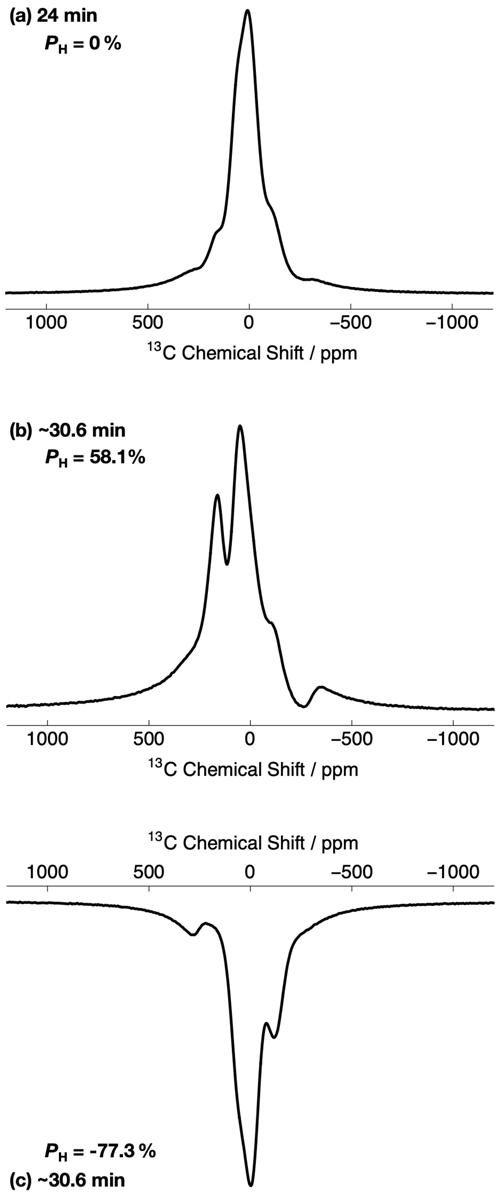
Figure 3 Relevant portions of the experimental ¹³C NMR spectra belonging to the ¹³C-labelled methyl group (¹³CH₃) of [2-¹³C]sodium acetate acquired at 7.05 T (¹H nuclear Larmor frequency = 300.13 MHz, ¹³C nuclear Larmor frequency = 75.47 MHz) and 1.2 K with a single transient (rf pulse flip angle = 3.5^∘) at two different ¹H DNP times. The labels indicate the ¹H DNP times at which the spectra were recorded. The timings coincide with those shown in Fig. 2. The ¹³C NMR spectra were acquired by using the rf pulse sequence depicted in Fig. 1. (a) No microwave irradiation; (b) positive microwave irradiation; and (c) negative microwave irradiation. All ¹³C NMR spectra have been scaled to yield the same maximum intensity.

However, the ¹³C NMR spectra become more complicated and gain sharper spectral features at extended ¹H DNP times; see Fig. 3b and c. At ∼ 30.6 min, the ¹³C NMR spectra are comprised of (at least) two main resonances with differing NMR signal intensities. In the case of positive microwave irradiation (Fig. 3b), the frequency separation between the two most intense ¹³C NMR peaks is ∼ 8.4 kHz, and the linewidth at FWHM is ∼ 17.7 kHz. It is interesting to note that the ¹³C NMR spectra acquired in the cases of positive (Fig. 3b) and negative (Fig. 3c) microwave irradiation do not have the same overall profile at long ¹H DNP times. These spectra correspond to much higher levels of ¹H polarization ($\left|P_{\mathrm{H}}\right|\mathit{\gtrsim }\mathrm{55}$ %).

3.3 ¹³C NMR peak normalized centre of gravity deviation vs. ¹H polarization

The DNP build-up curve for the ¹H polarization P_H as a function of the ¹H DNP time for positive microwave irradiation is shown in Fig. 4. More details regarding how to acquire such build-up curves are given in the following reference (Elliott et al., 2021b). The ¹H polarization build-up curve was found to have a stretched exponential behaviour, and the experimental data are well fitted with a stretched exponential function using a ¹H DNP build-up time constant denoted ${\mathit{\tau }}_{\mathrm{DNP}}^{+}$. Stretched exponential function: $A(\mathrm{1}-\exp \mathit{\{}-(t/{\mathit{\tau }}_{\mathrm{DNP}}^{+}{)}^{\mathit{\beta }}\mathit{\}})$, where A is a constant, ${\mathit{\tau }}_{\mathrm{DNP}}^{+}$ is the ¹H DNP build-up time constant extracted from the above fitting procedure and β is the breadth of the distribution of ¹H DNP build-up time constants. The mean ¹H DNP build-up time constant $〈{\mathit{\tau }}_{\mathrm{DNP}}^{+}〉$ is calculated as follows: $〈{\mathit{\tau }}_{\mathrm{DNP}}^{+}〉={\mathit{\tau }}_{\mathrm{DNP}}^{+}\mathrm{\Gamma }(\mathrm{1}/\mathit{\beta })/\mathit{\beta }$, where $\mathrm{\Gamma }(\mathrm{1}/\mathit{\beta })$ is the gamma function. A similar ¹H polarization build-up curve for the case of negative microwave irradiation, with parameters ${\mathit{\tau }}_{\mathrm{DNP}}^{-}$ and $〈{\mathit{\tau }}_{\mathrm{DNP}}^{-}〉$, is shown in the Supplement.

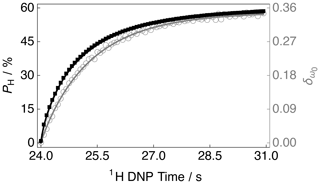
Figure 4 Experimental ¹H polarization P_H DNP build-up curve (black filled squares and left-hand axis) and ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ (grey empty circles and right-hand axis) as a function of the ¹H DNP time acquired at 7.05 T (¹H nuclear Larmor frequency = 300.13 MHz, ¹³C nuclear Larmor frequency = 75.47 MHz) and 1.2 K with a single transient per data point for the case of positive microwave irradiation. The timings coincide with those shown in Fig. 2. The black solid line indicates the best fit of the experimental data points for the ¹H polarization P_H DNP build-up curve, and has the corresponding fitting function: $A(\mathrm{1}-\exp \mathit{\{}-(t/{\mathit{\tau }}_{\mathrm{DNP}}^{\pm }{)}^{\mathit{\beta }}\mathit{\}})$. Mean ¹H DNP build-up time constant $〈{\mathit{\tau }}_{\mathrm{DNP}}^{\pm }〉=\mathrm{80.2}\pm \mathrm{0.3}$ s.

The sample polarized to P_H ≃ −77.3 % (¹H DNP time ≃ 30.6 min) by employing negative microwave irradiation with a ¹H DNP build-up time constant of $〈{\mathit{\tau }}_{\mathrm{DNP}}^{-}〉$ = 122.0 ± 0.4 s (β = 0.87). A reduced ¹H polarization of P_H ≃ 58.1 % was reached (at ¹H DNP time ≃ 30.6 min) by using positive microwave irradiation. The ¹H DNP build-up time constant was much shorter in this case: $〈{\mathit{\tau }}_{\mathrm{DNP}}^{+}〉$ = 80.2 ± 0.3 s (β = 0.77).

The ¹³C NMR line shapes presented in Fig. 3 are complicated and so it is desirable to construct a parameter which can describe the ¹H polarization P_H, be robust with respect to field inhomogeneities and easily applied to any line shape. Figure 4 therefore also displays the ¹³C NMR peak CoG deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ as a function of the ¹H DNP time for the case of positive microwave irradiation. The ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ is defined as

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}={\displaystyle \frac{M_{\mathrm{asym}}}{{\mathrm{LW}}_{\mathrm{0}}}},\end{array}$$

where M_asym is denoted as the first moment of asymmetry and corresponds to the following quantity:

$$\begin{array}{}\text{(2)}& M_{\mathrm{asym}}=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\left(\mathit{\omega }-{\mathit{\omega }}_{\mathrm{0}}(P_{\mathrm{H}}=\mathrm{0}\mathit{\%})\right)f\left(\mathit{\omega }\right)\mathrm{d}\mathit{\omega }.\end{array}$$

The first moment of asymmetry M_asym is based on a calculation whereby the CoG of the ¹³C NMR peak ω₀ is held constant at ω₀(P_H=0 %), i.e., the ¹³C NMR peak CoG corresponding to when the ¹H polarization P_H is zero. The CoG of the ¹³C NMR peak ω₀ is calculated as

$$\begin{array}{}\text{(3)}& {\mathit{\omega }}_{\mathrm{0}}=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathit{\omega }f\left(\mathit{\omega }\right)\mathrm{d}\mathit{\omega },\end{array}$$

where the intensities of the ¹³C NMR peaks are normalized as follows:

$$\begin{array}{}\text{(4)}& \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f\left(\mathit{\omega }\right)\mathrm{d}\mathit{\omega }=\mathrm{1},\end{array}$$

where ω is the resonance frequency, and f(ω) is the peak intensity at ω. The procedure outlined above ensures that M_asym=0 at P_H = 0 % such that the described approach can be readily generalized to any line shape. The quantity LW₀ is a measure of the linewidth of the ¹³C NMR peak in the case ofP_H = 0 %:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}& {\mathrm{LW}}_{\mathrm{0}}=\\ & \sqrt{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\left(\mathit{\omega }(P_{\mathrm{H}}=\mathrm{0}\mathit{\%})-{\mathit{\omega }}_{\mathrm{0}}(P_{\mathrm{H}}=\mathrm{0}\mathit{\%})\right)}^{\mathrm{2}}f\left(\mathit{\omega }(P_{\mathrm{H}}=\mathrm{0}\mathit{\%})\right)\mathrm{d}\mathit{\omega }},\end{array}\end{array}$$

i.e., the square root of the second moment at P_H = 0 %. This factor establishes a ¹³C NMR peak CoG deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ (defined in Eq. 1) which is a normalized and dimensionless quantity.

Figure 4 indicates that at longer ¹H DNP times, where the ¹H polarization P_H is higher, there is a greater ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$. Similar curves to those presented in Fig. 4 for the case of negative microwave irradiation are shown in the Supplement. It should be noted that the curve profiles and final values of ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ are not mirror images of each other. This is also reflected in the ¹³C NMR spectra acquired at ∼ 30.6 min; see Fig. 3. The rate of change in the value of ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ during the first ∼ 100 s of Fig. 4 indicates a more rapid change in the ¹H polarization P_H. This coincides with the starkest changes in ¹³C NMR line shape; see the Supplement.

The ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ as a function of the ¹H polarization P_H for positive microwave irradiation is shown in Fig. 5. The ¹H polarization P_H increases with an increasing ¹³C NMR peak CoG normalized deviation. The experimental data were fitted with a phenomenological relationship of the kind: $P_{\mathrm{H}}\left({\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}\right)=A\times {\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}^{\mathit{\beta }}$, where $P_{\mathrm{H}}\left({\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}\right)$ is the ¹H polarization as a function of the ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$, β is the order of the polynomial fit, and A is a scaling factor. The phenomenological function is simply used to correlate the ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ with the ¹H polarization P_H. The best fit values of the phenomenological function to the experimental data over the range of ¹³C NMR peak CoG normalized deviations shown in Fig. 5 are given in the caption.

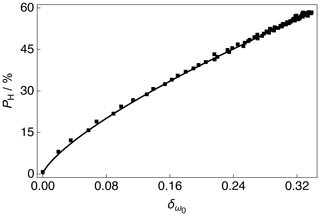
Figure 5 Experimental ¹H polarizations P_H as a function of the ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ acquired at 7.05 T (¹H nuclear Larmor frequency = 300.13 MHz, ¹³C nuclear Larmor frequency = 75.47 MHz) and 1.2 K with a single transient per data point for the case of positive microwave irradiation. The experimental data were fitted with a phenomenological function: $P_{\mathrm{H}}\left({\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}\right)=A\times {\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}^{\mathit{\beta }}$. The best fit values are A = 129.1 % ± 0.8 % and β = 0.736 ± 0.005. The absolute ¹H polarizations P_H were measured by comparison with a thermal equilibrium ¹H NMR signal.

4 Discussion

As discussed in Sect. 3.3, the CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ of the peaks in the ¹³C NMR spectrum indirectly provide the level of ¹H polarization P_H; see Fig. 5. It is unlikely that a uniform spin temperature between the ¹H and ¹³C nuclear spin reservoirs is reached at any time during the experiment presented in Fig. 1, but as long as a uniform spin temperature is achieved within the ¹H nuclear spin reservoir then the methodology presented above holds. It should be noted that the order of the polynomial fit β shown in Fig. 5 is likely to be influenced by the capabilities of the rf probe, such as the rf pulse homogeneity, and it is therefore recommended that (if possible) users implement similar measurements on their own experimental setups rather than simply reusing the value presented here. In this way, any laboratory can adopt the procedure and reproduce the result.

Once the ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ falls below zero the ¹H polarization P_H rapidly drops towards negative values; see the Supplement. This result implies that the NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ is less sensitive to negative microwave irradiation. This change in sensitivity of the ¹³C NMR peak CoG normalized deviations ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ to positive and negative microwave irradiation is also evident in the ¹³C NMR spectra; see Fig. 3 and the Supplement. This is likely associated with the following: (i) ¹³C NMR spectra at negative levels of ¹H polarization have line shapes with less pronounced features, i.e., partially unresolved peaks, and (ii) the ¹³C NMR line shape changes less dramatically as a function of negative ¹H polarization. These points could both be related to NMR line narrowing due to radiation damping for the case of negative microwave irradiation (Mao and Ye, 1997; Krishnan and Murali, 2013).

¹H polarizations in the range of 0 % ≲ P_H ≲ 30 % typically correspond to those accrued by ¹H DNP build-up experiments performed at liquid helium temperatures of 3.8–4.2 K. These results indicate that the ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ can therefore also be used to infer ¹H polarizations P_H accurately at elevated temperatures. However, the presence of methyl group rotation at temperatures above 1.2 K is likely to somewhat average the ¹H–¹³C dipolar couplings and could lead to a different trend compared with the fit presented in Fig. 5 (Latanowicz, 2005).

One possible contribution to the inflexion in the fit of the ¹³C NMR peak CoG normalized deviations ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ at low levels of ¹H polarization P_H is the presence of strong polarization gradients or highly polarized clusters of nuclear spins located within specific radii of the electron spins within the sample at short ¹H DNP times, which would lead to a non-uniform spin temperature. This contribution is expected to be minor.

The decay of ¹³C polarization during the ¹H DNP build-up interval $t_{\mathrm{DNP}}^{\mathrm{2}}$ shown in Fig. 2 occurs when the microwave source is active and the ¹³C nuclear spin ensemble relaxes towards the spin temperature it would have achieved in the case of direct ¹³C DNP, i.e., no CP. This ¹³C polarization decay is a combination of three factors: (i) the microwaves are active and hence polarization is diminishing towards the low DNP equilibrium of the ¹³C nuclear spins with TEMPOL as the polarizing agent; (ii) the ¹³C nuclear spins are being actively pulsed, although minimally, every 5 s, which leads to an accumulative loss of ¹³C NMR signal intensity over many minutes; and (iii) the radical concentration and temperature are in an optimal range for thermal mixing (Guarin et al., 2017), and since the ¹³C spins are polarized whilst the ¹H spins are saturated, the two nuclear pools most likely exchange energy via the electron non-Zeeman reservoir, which influences the time evolution of the ¹³C magnetization until the ¹H spins achieve the same spin temperature. The difference in the ¹³C polarizations P_C at ¹H DNP time = 24 min for positive and negative microwave irradiation is associated with the ¹H polarization build-ups and the performance efficiency of the multiple-contact CP rf pulses; see the Supplement.

The ¹³C NMR line shapes of [2-¹³C]sodium acetate shown in Fig. 3 have features which mainly originate from ¹³C chemical shift anisotropy (CSA) (max ∼ 1.5 kHz at our magnetic field of 7.05 T) and ¹H–¹³C dipolar couplings (typ. −22.7 kHz) that are affected by possible methyl group rotation. Since the ¹³C CSA is negligible with respect to the ¹H–¹³C dipolar couplings, it is assumed that the ¹H–¹³C dipolar couplings play the key role in the ¹³C NMR line shape of [2-¹³C]sodium acetate. The smaller ¹³C NMR peak contributions observed near the baseline in Fig. 3a likely correspond to different chemical environments within the sample which are being polarized on different timescales.

The values of ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$, P_H and the order of the polynomial fit β presented in Fig. 5 are likely to depend to a small degree on the solvent constituents. In the case of our sample, the glycerol-d₈ present in the dDNP glassing matrix yields an approximate ¹³C concentration of ∼ 410 mM at natural abundance, which is ∼ 14 % of the total ¹³C spin concentration. Under microwave irradiation, the natural abundance ¹³C spins of glycerol-d₈ will be polarized with their own build-up rate and maximum polarization, and although deuterated glycerol-d₈ can also be polarized by ¹H–¹³C CP (Vuichoud et al., 2014). As such, these contributions could impact the ¹³C NMR peak intensities, which would go some way to explaining why the ¹³C NMR spectra are not of the same overall profile under positive and negative microwave irradiation at long proton DNP times; see Fig. 3b and c. It is also possible that the dipolar couplings and CSA interactions manifest differently under positive and negative microwave irradiation, and there is a preferred energy state for coupling to positive and negative ¹H polarizations P_H leading to non-identical ¹³C NMR spectra.

The NMR spectra presented in Fig. 3 were acquired for the cases of high ¹³C SNRs, the largest of which is ca. 1244. In the event that CP cannot be (efficiently) implemented, and the acquired ¹³C NMR signal is weak, we anticipate that the method is robust with respect to a few kilohertz of line broadening, which can be used to improve the experimental SNR. The value of the ¹³C NMR peak CoG normalized deviation ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ is, however, likely to be sensitive to changes in phase, and this should therefore be taken into account before comparing experimental results to any calibration curves similar to those presented in Fig. 5. It is also possible that additional phase corrections may help the trend shown in Fig. 5 move closer to a linear fit for values of ${\mathit{\delta }}_{{\mathit{\omega }}_{\mathrm{0}}}$ < 0.02.

The results of this study suggest that other ¹³C-labelled molecules which might display distinct solid-state ¹³C NMR spectra, such as [1-¹³C]sodium formate and other ¹³CH₃ (or ¹³CH₂) group bearing molecular candidates (presence of a strong ¹H–¹³C dipolar coupling), could also be used as indirect ¹H polarization meters (polarimeters). To effectively polarize both ¹H and ¹³C nuclear spins, future experiments could use a tailored mixture of radical species, in certain cases. Clearly, at low levels of ¹H polarization P_H the lower-intensity resonance is unresolved and polluted by the more intense peak, and as such; the presented analysis could be further improved by considering Voigt fits of the complicated ¹³C NMR spectra, but since there are a number of resonances to consider this route would lead us away from our simple pedagogical approach.

5 Conclusions

We have demonstrated that ¹³C NMR line shape polarimetry of [2-¹³C]sodium acetate can be implemented to indirectly infer the ¹H polarization of the ¹³CH₃ group nuclear spins and potentially the whole sample if the constituents of which are sufficiently homogeneously mixed. An easy to implement protocol based on the normalized deviation of the centre of gravity of the ¹³C NMR peaks was employed and a simple relationship with ¹H polarization was found. This approach is complementary to traditional methods of measuring ¹H polarization, in suitable circumstances, and could be useful in situations where measurements of ¹H polarizations prove difficult, e.g., due to radiation damping (Mao and Ye, 1997; Krishnan and Murali, 2013), which can also likely impact the experimental data and order of the polynomial fit shown in Fig. 5. Other appropriate cases for potential implementation include the following: (i) the lack of a ¹H rf coil, (ii) the presence of large background signals and (iii) the absence of a thermal equilibrium spectrum. The approach presented here works well for traditional dDNP-compatible sample formulations, but future studies employing fully deuterated dDNP solutions could provide ¹³C NMR line shapes with more distinct features.